1. INTRODUCCIÓN
En la actualidad, la demanda de servicios de comunicaciones inalámbricas ha crecido de manera exponencial, lo cual ha producido que se hable de una saturación del espectro [1], situación que no necesariamente es correcta, dado que existen bandas de frecuencias que están siendo sub utilizadas [2], donde el ejemplo más evidente son las bandas asignadas para la prestación del servicio de televisión.
Por lo tanto, existen huecos espectrales que en algunos casos son permanentes, y en otros, se producen en determinados momentos sobre algunas bandas de frecuencia; lo cual implica un dilema, ya que por un lado, los usuarios de algunos servicios como los móviles, no cuentan con la suficiente cantidad de espectro para transmitir, pero de otra parte, algunas bandas espectrales no se encuentran completamente en uso [2].
Como una propuesta de solución al problema de sub-utilización del espectro derivado de la aplicación de políticas de asignación fija de espectro, surge el concepto de Asignación Dinámica de Espectro (DSA) [3]; en el cual, desde la perspectiva de un modelo de acceso al espectro jerárquico oportunista, es necesario desarrollar una técnica que permita la identificación rápida y precisa de los huecos espectrales.
Es por ello que surge un concepto más amplio como lo es Radio Cognitivo (CR), el cual fue propuesto en [4], como una tecnología promisoria para explotar el espectro sub-utilizado de manera oportunista, permitiendo a los Usuarios Secundarios (SU) utilizar el espectro asignado a los Usuarios Primarios (PU) cuando estos últimos no se encuentren activos.
Para hacer esto, los SU requieren realizar de manera permanente el sensado de espectro, es decir, detectar la presencia o no de señal en el canal de comunicaciones; si se detecta que no existen usuarios primarios haciendo uso del espectro, el SU puede considerar que el canal sensado probablemente sea una oportunidad de espectro [3].
El sensado de espectro es una función fundamental en CR, sin embargo, existen factores que hacen que el sensado de espectro sea un reto, algunos de ellos son: Relación Señal a Ruido (SNR) la cual puede ser muy baja del orden de los -20dB, como por ejemplo, las señales provenientes de micrófonos inalámbricos que operan en la banda de TV; desvanecimiento multitrayectoria, que puede causar fluctuaciones del nivel de la señal del orden de 20 a 30dB; adicionalmente el ruido y la interferencia, pueden presentar niveles variantes con el tiempo, lo cual genera incertidumbre en la detección[5].
Para realizar la función de sensado de espectro, se han propuesto varios métodos, dentro de los cuales se encuentran, prueba de tasa de verosimilitud (LRT) [9], detección de energía [6]–[11], filtraje adaptado [7], [9], [11], [12] y detección por características ciclo-estacionarias [13]–[15] entre otros; cada método presenta ventajas y desventajas, por ejemplo, LRT se ha probado que es óptimo [9], sin embargo no es práctico debido a que requiere conocimiento exacto de la información del canal y de las distribuciones de probabilidad de la fuente de señal y de ruido; la detección por filtraje adaptado, requiere conocimiento perfecto de las características del canal y sincronización; el método basado en características cicloestacionarias, necesita conocimiento de las frecuencias cíclicas de los usuarios primarios y presenta una gran complejidad computacional [7]; el método basado en detección de energía no requiere información a priori de la señal o del canal, presentando como ventaja una robustez frente al desvanecimiento, sin embargo, requiere conocimiento de la potencia de ruido, lo cual hace que malas estimaciones de la potencia de ruido conduzcan a limitaciones de eficiencia con baja SNR y altas probabilidades de falsa alarma [6]–[8], [11], [16].
Dentro de las técnicas de sensado de espectro, la descomposición en valores singulares SVD [17], ofrece un nuevo campo de estudio, proyectándose como un camino prometedor para la futura implementación de radio cognitiva, es así como en los últimos años se han realizado investigaciones, como se muestra en [18] [19] [20].
Sin embargo, dichas investigaciones presentan resultados obtenidos bajo las condiciones requeridas por el teorema de muestreo de Nyquist [21], lo cual implica que, para realizar la detección de las bandas elevadas del espectro radioeléctrico, la alta complejidad en el procesamiento del detector, impide su implementación práctica, todo esto en el ámbito monobanda.
En este artículo, se presenta un método experimental, alternativo para el sensado monobanda de señales continuas, basado en SVD, con muestreo sub-Nyquist.
1. VALORES SINGULARES DE MUESTRAS DE SEÑALES CONTINUAS
1.
Para la aplicación del método propuesto en este artículo, es necesario identificar el comportamiento de los valores singulares de señales continuas.
A. Comportamiento de valores singulares:
Dentro de los parámetros importantes que modifican las características de los valores singulares tales como su máximo valor entre otros, están: el número de muestras, y la frecuencia de muestreo.
En las figuras 1 a 4 se presentan la variación de los valores singulares de la matriz de muestras de una señal senoidal. Las dos primeras figuras (1 y 2) indican los resultados obtenidos para diferentes frecuencias de muestreo, mientras que las figuras 3 y 4, presentan los resultados con un número mayor de muestras. Se evidencia que, como se aprecia en las figuras, los valores singulares de la matriz de autocorrelación de la señal, tanto para muestreo a la tasa de Nyquist, como para muestreo subNyquist, presentan magnitudes aproximadamente iguales, dicha aproximación mejora con un mayor número de muestras obtenidas, lo cual no necesariamente implica una mayor frecuencia de muestreo, pero si, un mayor intervalo de tiempo de muestreo, que debe ser comparable con el tiempo de trama del estándar de comunicaciones a sensar.
En las gráficas, los marcadores representan los valores singulares obtenidos a frecuencias subNyquist (gris claro), estrictamente Nyquist (negro) y over-Nyquist (gris oscuro).
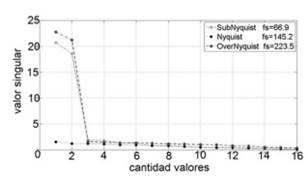
Fig.1: Valores singulares, señal senoidal frecuencia central 72,61, frecuencias de muestreo sub= 66,93, Nyq=145,22 y over=223,50. Obtenidos a partir de 32 muestras. Fuente: Autores.
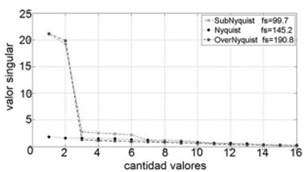
Fig.2: Valores singulares, señal senoidal frecuencia central 72,61, frecuencias de muestreo sub= 99,66, Nyq=145,22 y over=190.78. Obtenidos a partir de 32 muestras. Fuente: Autores.
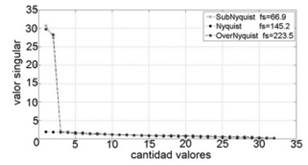
Fig.3: Valores singulares, señal senoidal frecuencia central 72,61, frecuencias de muestreo sub= 66,93, Nyq=145,22 y over=223,50. Obtenidos a partir de 64 muestras. Fuente: Autores.
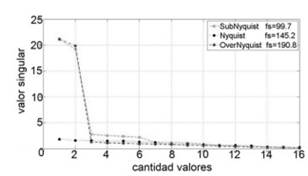
Fig.4: Valores singulares, señal senoidal frecuencia central 72,61, frecuencias de muestreo sub= 99,66, Nyq=145,22 y over=190.78. Obtenidos a partir de 64 muestras. Fuente: Autores.
B. Distribución de los máximos valores singulares:
Teniendo en cuenta la diferencia significativa existente entre los máximos valores singulares, obtenidos a frecuencias sub, over, y estrictamente Nyquist, se procedió a extraer los máximos valores singulares de la matriz de muestras de señales senoidales, cuyas frecuencias centrales se se obtuvieron de forma aleatoria (con distribución uniforme).
Con los resultados, se identificó la distribución que presentan los máximos valores singulares para frecuencias sub-Nyquist comprendidas en el intervalo de la ec. 1:
Las figuras 5 y 6, muestran la distribución de los máximos valores singulares para dos frecuencias de muestreo sub-Nyquist.
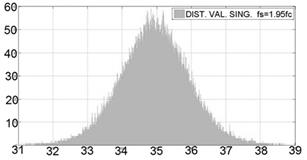
Fig 5: Distribución de los máximos valores singulares de señales senoidales con diferentes valores de frecuencia central fc, y frecuencia de sub-muestreo fs=1,95fc. Fuente: Autores.
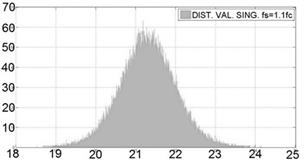
Fig 6: Distribución de los máximos valores singulares de señales senoidales con diferentes valores de frecuencia central fc, y frecuencia de sub-muestreo fs=1,1fc. Fuente: Autores.
C. Datos estadísticos:
La distribución de los máximos valores singulares (M.V.S) para diferentes frecuencias de submuestreo, pueden aproximarse a una distribución normal [22], descrita por su valor de media y su varianza.
M. V. S~N(µ, a) (2)
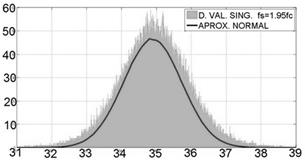
Fig 7: Aproximación a distribución normal con
µ = 34.94 y a = 0.69. Fuente: Autores.
Los valores de media de la ec. 2, varían dependiendo del valor de la frecuencia de submuestreo, como se indica en la tabla 1, donde se presentan
Tabla 1. Variación de µ para cuatro frecuencias de submuestreo. Fuente: Autores.
|
fs |
µ (media) |
|
1.99 fc |
11,3714 |
|
1.95 fc |
34,9390 |
|
1.50 fc |
21,8901 |
|
1.10 fc |
21,2991 |
Teniendo en cuenta estos datos estadísticos, se gráfica el comportamiento de la media de los máximos valores singulares para diferentes frecuencias de submuestreo.
Fig. 8: Comportamiento de la media de los máximos valores singulares de señales senoidales para diferentes frecuencias de sub-muestreo comprendidas en el intervalo [fc,2fc]. Fuente: Autores.
En la figura 8, el eje de las abscisas representa el decremento frecuencial de fs respecto al valor estricto de Nyquist, es decir, a medida que aumenta el porcentaje de decremento, la señal es submuestreada con frecuencias cada vez mucho menores, alejándose de fs=2fc y acercándose al valor de frecuencia central de la señal (fc). Cada punto muestra el máximo valor singular para cada frecuencia de submuestreo, al cual tiende la señal en presencia de ruido.
3. MÉTODO DE ESTIMACIÓN
Para estimar la frecuencia de la señal a través del método propuesto, el procedimiento es el siguiente:
A. Señal adquirida:
Esta se compone de la señal a la cual se le estimará la frecuencia central x(t), mas ruido blanco aditivo gaussiano x(t)
y(t)=x(t)+r(t) (3)
B. Muestreo:
La señal es muestreada con una frecuencia menor a la establecida por el teorema de Nyquist, es decir, con una frecuencia menor al doble de la frecuencia central de dicha señal, ec. 4:
Obteniendo como resultado un vector de muestras,presentado en la ec. 5:
En esta, el vector y(m) denota que ha sido obtenido bajo muestreo sub-Nyquist, respetando las notaciones presentes en la diversa bibliografía, en las cuales los vectores con representación p(n) se obtienen bajo las condiciones del teorema de muestreo [21].
C. Autocorrelación:
A partir del vector de muestras ec. 5, se calcula la matriz de autocorrelación [23], ec. 6.
Teniendo en cuenta las propiedades implícitas en el ruido blanco gaussiano (ruido no correlacionado con la señal, la matriz obtenida presenta valores relacionados principalmente con la señal a detectar, siendo los valores relacionados al ruido cercanos a cero (ruido no correlacionado),ec. 7, permitiendo realizar un filtrado implícito al proceso de autocorrelación.
D. SVD:
Se aplica el método de descomposición en valores singulares a la matriz de autocorrelación. Posteriormente, se obtiene su máximo valor singular.
E. Comparación:
El valor 
es
comparado con la media de las distribuciones de probabilidad que presentan los máximos
valores singulares, obtenidos a diferentes frecuencias sub-Nyquist,
comprendidas en el intervalo mostrado en la ec. 1, y con la misma SNR, ec. 9.
F. Estimación:
Según la
ubicación del valor de media próximo al valor 
, se estima
la frecuencia central de la señal. La diferencia con métodos basados en Pseudo espectro,
como lo son Music [24] y Pisarenko [25], es que, en estos métodos, el análisis
se realiza con muestras adquiridas bajo el teorema de muestreo, además, el
proceso de estimación realizado en dichos métodos, se basa en la ortogonalidad presente
entre un vector de frecuencias base y los autovectores de la matriz de
muestras. Por otra parte, el método propuesto está basado, principalmente, en
la comparación del máximo valor singular, con la media de los valores
singulares previamente obtenidos, presentados en la figura 8.
La figura 9 representa el método propuesto en este artículo. En esta, se describe gráficamente cada proceso mencionado anteriormente, mientras que el diagrama de flujo del proceso de estimación es mostrado en la figura 10.
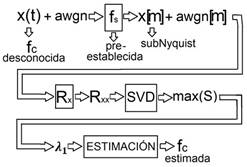
Fig. 9: Diagrama de bloques, Método propuesto Fuente: Autores
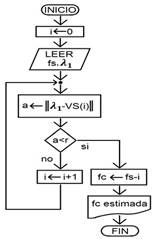
Fig. 10:Estimacion de frecuencia Fuente: Autores.
4. RESULTADOS
Se colocó a prueba el método de estimación propuesto, con señales senoidales de diferentes frecuencias inmersas en ruido blanco gaussiano, con una SNR igual a 12dB, obteniendo como resultados los siguientes datos: Tabla 2:
Resultados de pruebas del método de estimación, fs frecuencia de muestreo, fc frecuencia central de la señal, fcalc frecuencia calculada con el método. Fuente: Autores.
|
fs |
fc |
fcalc |
%error |
|
1590 |
834 |
832,4607 |
0,18 |
|
341 |
187 |
187,3626 |
0,19 |
|
611 |
332 |
333,8798 |
0,57 |
|
671 |
576 |
424,6835 |
26,27 |
|
427 |
230 |
234,6154 |
2,01 |
|
117 |
113 |
75 |
33,63 |
|
605 |
336 |
472,6563 |
40,67 |
|
1203 |
902 |
1002,5 |
11,14 |
|
1054 |
694 |
563,6364 |
18,78 |
|
487 |
342 |
340,5594 |
0,42 |
|
782 |
625 |
610,9375 |
2,25 |
|
1440 |
838 |
878,0488 |
4,78 |
|
170 |
106 |
147,8261 |
39,46 |
|
492 |
288 |
258,9474 |
10,09 |
|
210 |
198 |
165,3543 |
16,49 |
|
1219 |
715 |
944,9612 |
32,16 |
|
1413 |
774 |
763,7838 |
1,32 |
|
537 |
322 |
284,127 |
11,76 |
|
226 |
220 |
207,3394 |
5,75 |
|
200 |
128 |
131,2500 |
2,54 |
|
194 |
180 |
129,3333 |
28,15 |
|
179 |
165 |
102,2857 |
38,01 |
|
617 |
536 |
482,0313 |
10,07 |
|
201 |
153 |
157,0313 |
2,63 |
|
329 |
262 |
238,4058 |
9,01 |
|
895 |
645 |
778,2609 |
20,66 |
|
735 |
577 |
448,1707 |
22,33 |
|
775 |
545 |
673,913 |
23,65 |
|
1464 |
1170 |
1143,8 |
2,24 |
Tabla 3. Continuación de resultados obtenidos.
|
fs |
fc |
fcalc |
%error |
|
2822 |
1642 |
1720,7 |
4,79 |
|
37 |
23 |
19,7861 |
13,97 |
|
756 |
425 |
460,1266 |
8,27 |
|
242 |
228 |
200 |
12,28 |
|
2335 |
1370 |
1768,9 |
29,12 |
|
2739 |
1500 |
1480,5 |
1,30 |
|
835 |
501 |
421,7172 |
15,82 |
|
1515 |
786 |
769,0355 |
2,16 |
|
1715 |
1098 |
1092,4 |
0,51 |
|
2680 |
1571 |
1549,1 |
1,39 |
|
3257 |
1699 |
1770,1 |
4,18 |
Teniendo en cuenta los resultados consignados en las tablas 2 y 3, se observó que, para frecuencias de muestreo cercanas a la frecuencia central de la señal, es decir, la relación entra la frecuencia de muestreo y frecuencia central ubicada en el intervalo de la ec. 9, el error supera el 25%.
Para frecuencias de muestreo que cumplen la relación ubicada dentro del intervalo de la ec. 10. El error no supera el 25%.
Para facilitar el análisis de los resultados se realizó el histograma de los porcentajes de errores.
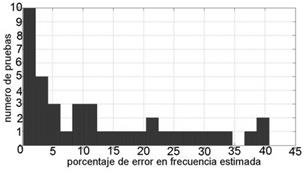
Fig 11: Histograma de los porcentajes de error, obtenidos para 40 señales senoidales de diferentes frecuencias. Fuente: Autores.
(11)
5. CONCLUSIONES
En este artículo se propone un novedoso método de sensado de espectro local para dispositivos de CR basado en muestreo sub-Nyquist, el cual no requiere conocimiento apriori de las características de la señal presente en el entorno de radio, demostrándose que mediante el método propuesto es posible realizar la función de sensado de espectro utilizando una cantidad de muestras menor a las obtenidas a la tasa de Nyquist y sin conocimiento apriorí de las características de la señal, así mismo se evidencia que
· Los porcentajes de error, se encuentran dentro de parámetros aceptables, teniendo en cuenta el submuestreo realizado, y el número de muestras de la señal adquirida.
· Para disminuir dichos porcentajes, se requieren mayor número de muestras de la señal, es decir,extender el tiempo de adquisición de la señal sin necesidad de modificar las frecuencias de submuestreo.
· El método propuesto, puede implementarse en sistemas de bajo rendimiento, obteniendo así, sistemas de sensado monobanda con muestreo sub-Nyquist de bajo costo.
· El método de descomposición en valores singulares se presenta como una gran herramienta matemática dentro del análisis de señales, estableciendo un nuevo campo de investigación.
6. aGRADECIMIENTOS
Muchos agradecimientos al programa de maestría en electrónica y telecomunicaciones de la Universidad del Cauca, por todos los conocimientos brindados, durante esta formación postgradual.
Un agradecimiento especial al director de mi tesis, y coautor de este artículo, que con todo su apoyo, conocimiento y dirección, me dirige en el camino de la investigación.
7. REFERENCIAS BIBLIOGRÁFICAS
[1] J. F. Negrete, E.Páez, G. I. Sánchez, and J. Bravo, " Spectrum Crunch a la Vuelta de la Esquina," MediaTelecom, Tech Rep., May. 2013.
[2] M. A. McHenry, D. McCloskey, D. Roberson, and J. T. McDonald, " Spectrum Occupancy Measurements Chicago, Illinois," Tech Rep., Nov. 2005.
[3] Q. Zaho, B. M. Sadler, “A Survey of Dynamic Spectrum Access: Signal Processing, Networking and Regulatory Policy”, IEEE Signal Processing Magazine, pp. 79 – 89, May 2007.
[4] J. Mitola, “Cognitive radio for flexible mobile multimedia communications,” in Proc. IEEE Int. Workshop Mobile Multimedia Communications, pp. 3–10, 1999.
[5] D. Cabric, S.M. Mishra, and R.W. Brodersen, “Implementation issues in spectrum sensing for cognitive radios,” in Proc. 38th. Asilomar Conf. Signals Systems, Computers, pp. 772–776, 2004.
[6] A. Sonnenschein and P. M. Fishman, “Radiometric detection of spreadspectrum signals in noise of uncertainty power,” IEEE Trans. Aerosp. Electron. Syst., vol. 28, no. 3, pp. 654–660, Jul. 1992.
[7] A. Sahai, D. Cabric, “Spectrum sensing: Fundamental limits and practical challenges,” A tutorial in IEEE Int. Symp. New Frontiers DySPAN, Baltimore, MD, Nov. 2005.
[8] R. Tandra and A. Sahai, “Fundamental limits on detection in low SNR under noise uncertainty,” in Proc. WirelessCom, Maui, HI, Jun. 2005, pp. 464– 469.
[9] S. M. Kay, Fundamentals of Statistical Signal Processing: Detection Theory, vol. 2. Englewood Cliffs, NJ: Prentice–Hall, 1998.
[10] H. Urkowitz, “Energy detection of unknown deterministic signals,” Proc. IEEE, vol. 55, no. 4, pp. 523–531, Apr. 1967.
[11] D. Cabric, A. Tkachenko, and R. W. Brodersen, “Spectrum sensing measurements of pilot, energy, and collaborative detection,” in Proc. MILCOM, Oct. 2006, pp. 1–7.
[12] H.-S. Chen, W. Gao, and D. G. Daut, “Signature based spectrum sensing algorithms for IEEE 802.22 WRAN,” in Proc. IEEE ICC, Jun. 2007, pp. 6487–6492.
[13] W. A. Gardner, “Exploitation of spectral redundancy in cyclostationary signals,” IEEE Signal Process. Mag., vol. 8, no. 2, pp. 14–36, Apr. 1991
[14] W. A. Gardner,W. A. Brown, III, and C.-K. Chen, “Spectral correlation of modulated signals— Part II: Digital modulation,” IEEE Trans. Commun., vol. COM-35, no. 6, pp. 595–601, Jun. 1987.
[15] N. Han, S. H. Shon, J. O. Joo, and J. M. Kim, “Spectral correlation based signal detection method for spectrum sensing in IEEE 802.22 WRAN systems,” in Proc. Int. Conf. Advanced Commun. Technol., Phoenix Park, Korea, Feb. 2006, pp. 1765–1770.
[16] S. Shellhammer and R. Tandra, Performance of the Power Detector With Noise Uncertainty, Jul. 2006, IEEE Std. 802.22-06/0134r0.
[17] J. J. Martínez, "La Descomposición en Valores Singulares (SVD) y Algunas de sus Aplicaciones," La Gaceta de la RSME, vol 8 no. 3 pp. 795-810, 2005.
[18] M. F. Fahim and M. S. Raeen, "SVD Detection for Cognitive Radio Network based on Average of Maximum-Minimum of the ICDF," Internal. Journ. Adv. Comp. Research, vol. 2, no. 3, pp. 182-187, Sep 2012.
[19] M.Hasbullah and H.Suhaidi, "SVD-Based Signal Detector for Cognitive Radio Networks," in 13th Internal. Confer. Modell.and Simul., 2011, pp. 513-517.
[20] N. Chouhan, J. Dipti, and S.V. Charhate, "Cooperative Spectrum Sensing signal detection using SVD Signal Detector for Cognitive Radio," ITSI Transactiosn on Electrical and Electronics Engineering, pp. 31 - 34, 2013.
[21] C.Shannon, "Communication in the presence of noise," Proc. IEEE, vol. 72, no. 9, pp. 1192-1201, Sep. 1984.
[22] G. Castellanos Domínguez and Y. Semenovich Shinakov, " Analisis de Aleatoriedad en Señales y Sistemas," Universidad Nacional de Colombia, Sede Manizales. 2007
[23] J. G. Proakis and D. G. Manolakis, " Digital Signal Processing," Pretience Hall International, Inc. 1996.
[24] Stoica and A. Nehorai, “Statistical efficiency study of direction estimation methods, Part I: Analysis of MUSIC and preliminary study of MLM,” Advances in Spectrum Analysis and Array Processing, S. Haykin, Ed. Englewood Cliffs, NJ: Prentice-Hall, vol. 1, pp. 263-305, 1991.
[25] V.F. Pisarenko, “The retrieval of harmonics from a covariance function'', Geophysics J.Royal Ast. Soc., vol.33, pp.347-366, 1973.