1. INTRODUCCIÓN
El paradigma de desarrollo de software orientado por objetos (OO) [1][2][3][4] es ampliamente usado durante las fases de análisis, diseño e implementación de un proyecto de software.
En este paradigma las especificaciones OO procuran estructurar los elementos del software de la misma manera que se estructuran los elementos del área de aplicación, lo que facilita tanto su elaboración como su discusión con los interesados en resolver los problemas del área.
Dentro de los lenguajes de especificación OO, el lenguaje UML [5] se ha impuesto como el estándar de facto para las fases de análisis y diseño de la mayoría de los desarrollos de software. En UML las especificaciones se apoyan en un conjunto de primitivas gráficas que permiten modelar el área de aplicación y el software, por medio de diagramas asociados con las diferentes fases de análisis y de diseño.
Entre los diagramas de UML, el diagrama de clases (DC) ocupa un lugar destacado ya que describe y estructura los datos asociados con el área de aplicación y el software. Al definir y describir dichos datos, el DC se convierte en un elemento esencial para la definición de la Base de Datos (BD) del software. En efecto, aunque el DC no se debe considerar como una definición de la BD1 , sí establece un conjunto de restricciones sobre la misma.
En consecuencia, para definir el DC apropiado para un problema, el modelador necesita entender de forma precisa el significado (o semántica [6][7]) de los DCs y de las restricciones sobre la BD que este determina.
Para darle un significado preciso al paradigma OO, se han propuesto varias formalizaciones del modelo OO de UML, y en particular del DC. La motivación de estas formalizaciones es diversa y determina el tipo mismo de la formalización, así:
· Extender la expresividad de la notación gráfica para incorporar las restricciones del área de aplicación al modelo. Este es un objetivo que satisfacen prácticamente todas las formalizaciones. Vale la pena destacar que un enfoque para lograr este único fin es el de aumentar el lenguaje OO, con notaciones lógicas especializadas, tales como el Object Constraint Language (OCL) [8] y el VDM++ [9] [10].
· Facilitar el análisis y verificación de los DC por medio de un sistema de demostración automatizado. Para ello, en [11][12][13] [14][15] y [16] se describe tanto al DC como a sus restricciones, usando la notación formal Z [17]. En [18] y [19], se lleva a cabo la misma tarea en lógica descriptiva [20].
· Soportar el refinamiento y la verificación formal del software. Para ello en [21], [22] y [23], se propone transformar las especificaciones OO al lenguaje formal B.
· Definir la semántica del DC. Para ello en [11][12][13][14] y [15], luego de la descripción y verificación del DC, se procede a representar, mediante la notación Z, el conjunto de estructuras de valores que constituye el dominio semántico de una especificación UML, denominado como “System Model” (y que representa el conjunto de todas las posibles BD abstractas); para luego, definir una función que proyecta la representación en Z del DC al subconjunto del System Model que constituye su semántica. (o sea el conjunto de las BD abstractas descritas por el DC).
· Soportar la evolución de los modelos UML. Para ello en [24] se presenta una formalización del meta modelo de UML.
· Una alternativa clásica para la definición de la semántica del DC, --sin necesidad de describirlo en una lógica--, es la de transformarlo directamente a una teoría en dicha lógica considerándolo como una representación simplificada de dicha teoría, i.e., “azúcar sintáctico” [25]. Desde este enfoque, la semántica de un DC es simplemente la semántica de la teoría que le corresponde en la lógica. Este enfoque es usado en [26] para el DC de UML usando la notación Z, en [27] para OMT usando Larch [28] y sugerido en [24] UML usando el lenguaje Maude [29].
En nuestra experiencia con recién llegados al área del desarrollo de software, al intentar precisar la semántica del DC desde la óptica de la lógica, se han identificado problemas con las referidas formalizaciones, en particular:
· Las formalizaciones centradas en definir la semántica del DC ([11][12][13][14] y [15]), además de usar una notación lógica compleja ([17]), parten de la representación previa del DC en la misma lógica (el meta modelo del DC en la lógica), complicando la especificación de la función que proyecta el DC al subconjunto del System Model que constituye su semántica.
· Las notaciones asociadas con las formalizaciones referidas en el párrafo anterior, no facilitan la representación de los elementos del dominio semántico, dificultando la ejemplificación de casos pertenecientes a la semántica de un DC.
Para resolver estos problemas, se ha recurrido a una formalización del DC desde un enfoque clásico traduciéndolo a una teoría en una lógica matemática con una semántica claramente definida.
Con ello no solo queda definida la semántica del DC sino que queda abierta la puerta para usar dicha traducción para analizar y verificar un DC en el marco de la lógica seleccionada. Esto último es consecuencia de que la especificación del DC [5] es en sí misma una instancia del DC (el meta modelo del DC en un DC), y por tanto bastaría con traducir este meta modelo a la lógica para llevar a cabo el análisis y la verificación de un DC cualquiera en el marco la misma.
Nótese además, que una vez traducido el meta modelo a una teoría (o meta teoría), un elemento de su semántica, es isomorfo con un DC y; por lo tanto; se podría traducir ya sea al DC en su forma gráfica o a la teoría que le corresponde para definir su propia semántica.
La lógica seleccionada para la traducción fue una lógica ecuacional de primer orden. La selección de dicha lógica se debe a que su dominio semántico se expresa fácilmente en el marco de la teoría de conjuntos siendo la semántica de un DC un conjunto de conjuntos de tuplas (asimilables a un conjunto de tablas), sobre las que pesan las restricciones especificadas en el DC.
La notación seleccionada fue la del lenguaje de programación funcional Maude [29], que implementa una lógica de rescritura que subsume la lógica ecuacional. Como lógica y a la vez lenguaje de programación, Maude permitirá obtener en trabajos futuros, beneficios como los siguientes:
· La traducción de un DC ejecutará, permitiendo animar, e.g., consultas a una BD expresada como un término del lenguaje.
· La satisfacción por parte de una BD de las restricciones que el DC impone a las clases y a sus relaciones podrá ser verificada automáticamente por el gestor de tipos del lenguaje.
· La traducción del meta modelo permitirá analizar, verificar y animar los DC, expresados como términos del lenguaje, traducibles a las teorías del lenguaje que representan.
En este enfoque, un DC no es más que la especificación de una serie de Tipos Abstractos de datos (TAD) y una BD un conjunto de términos de dichos TADs. En particular la notación de Maude permite representar:
· Las instancias de la BD como evocaciones base de los operadores constructores de los TAD.
· La navegación entre los objetos.
·
En este artículo se presentan entonces los elementos básicos de la formalización del DC en Maude, ilustrándolos con un caso de estudio. El contenido del artículo es el siguiente: en la Sección 2 se presenta una breve descripción de la notación Maude. En las secciones 3 y 4 se presentan los TADs asociados con las clases y con las relaciones de un DC. En la Sección 5 se presentan los TADs asociados con los conjuntos de instancias de las clases y relaciones. En la Sección 6, se presenta el TAD asociado con el DC. En la
Sección 7 se presentan los elementos que definen el significado de la herencia. En la Sección 8 se presentan las conclusiones y se propone el trabajo futuro
2. EL LENGUAJE MAUDE
El lenguaje Maude [29] permite crear especificaciones formales algebraicas para TADs [30]. El intérprete de Maude permite además, “animar” la especificación llevando a cabo el cálculo de términos, por medio de un proceso de reescritura dirigido por las ecuaciones de la especificación, que constituyen un sistema de reescritura de términos [32], [33].
Una especificación en Maude contiene planteamientos de varios TADs. Cada planteamiento se inicia con una palabra clave que indica su TAD. En esta especificación serán necesarios los TADs de planteamiento que se explican a continuación
· Declaración de TAD: Usado para declarar un TAD. En Maude sort es sinónimo de TAD: sort <id-sort>.
· Declaración de operador: Usado para declarar el perfil de los operadores: op <plantilla> : <srts-dom> -> <srt-ran> . [<atrop>]. .
· Declaración de variables: Usado para declarar los nombres de las variables y su respectivo TAD: vars <lst-var> : <id-sort>. .
· Ecuación incondicional: Se declara mediante la palabra clave eq, seguida de un término (denominado lado izquierdo), el símbolo de igualdad =, y un término (denominado lado derecho) y se finaliza con un punto: eq <t1> = <t2>. .
· Ecuación de membresía condicional: Usada para indicar que el TAD del témino <t2> representa instancias del TAD <id_sort> si <t3> evalúa verdadero: cmb <id-sort>: <t2> if <t3>. .
Donde:
<id-sort>: Es el nombre del TAD. <plantilla>:
Es un nombre de operador. Puede además tener una lista de caracteres “_” (entre <> y separados por comas) para indicar la posición de los operandos (notación infija).
<srts-dom>: Es una lista de cero o más nombres de TADs, que indican el TAD de los argumentos del operador.
<srt-ran>: Es un nombre de TAD que identifica el TAD del resultado de evocar el operador. [<atr-op>]: Es una secuencia de cero o más propiedades del operador (e.g., la propiedad ctor identifica a los operadores constructores). <lst-var>: Es una lista de nombres de variables. <t1><t2><t3>: Son términos.
3. TAD ASOCIADO CON LAS CLASES
Cada clase del DC especifica un TAD que se puede expresar en Maude como se describe a continuación.
En la Figura 1 se muestra el DC (se usa la notación propuesta en [5]), de una aplicación para una agencia de publicidad que usa una página web para presentar álbumes fotográficos de sus usuarios: En dicho diagrama se encuentran las clases Persona, Usuario, Álbum e Imagen, cada una con un conjunto de atributos relevantes para el dominio de la aplicación.
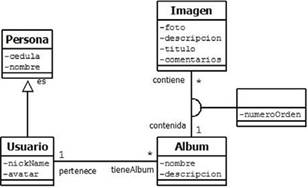
Fig. 1. Diagrama de Clases
3.1 Sort asociado con una clase del DC
El nombre de una clase, hace referencia a un TAD asociado con la clase. Este TAD contiene el conjunto de todas las posibles instancias de dicha clase. Para el caso de estudio, estos TADs son los siguientes:
sort Persona.
sort Usuario.
sort Album.
sort Imagen.
3.2 Constructor del TAD asociado con una clase
Las posibles instancias de una clase son todas las posibles tuplas que se pueden formar con los valores de los atributos de dicha clase. Para representar estas instancias, la formalización provee un operador constructor, que permite especificar una tupla de valores para los atributos, rotulada con el nombre de la clase. Para el caso de estudio se tienen los siguientes constructores:
op persona<_,_> :
Int String -> Persona . [ctor].
op usuario<_,_,_> :
Persona String String -> Usuario . [ctor].
op album<_,_> :
String String -> Album . [ctor].
op imagen<_,_,_,_> :
String String String String -> Imagen . [ctor].
Nótese que el constructor expresa que el TAD asociado con la clase es esencialmente el producto cartesiano de los TADs de sus atributos.
Por medio del constructor es posible referirse acualquiera de las instancias de la clase. En efecto, una instancia de la clase es un término base del constructor. Así, son instancias de las clases del ejemplo los términos siguientes:
persona<1,"Joe”>.
usuario<persona<1,"Joe">,
"JoeelMalo”,”AvtJoe.jpg”>.
album<"Joe","profe">. album<"Perú","Inca">.
imagen<"faro.jpg","Faro en el fin del mundo",
"El Faro","Sin comentarios">.
3.2 Selectores con la notación punto para los TADs asociados con las clases
En una especificación OO con frecuencia es necesario referirse al valor de los atributos de las instancias de la clase. Para ello los lenguajes OO ofrecen la notación [objeto].[atributo]. Para mantener esta notación, la formalización provee un conjunto operadores selectores de la forma _.[nombre-atributo] que tienen como dominio el TAD asociado con la clase y como rango el TAD asociado con el atributo. Para el caso de estudio dentro del conjunto de selectores están los siguientes operadores:
vars Nom Desc : String.
op _.nombre : Album -> String.
op _.descripcion : Album -> String.
eq album<Nom,Desc>.nombre = Nom.
eq album<Nom,Desc>.descripcion = Desc.
Ejemplos album<"Joe","profe">.nombre
= "Joe".
album<"Perú","Inca">.descripcion
= "Inca".
4. TAD ASOCIADO CON LAS RELACIONES ENTRE CLASES
Cada relación del DC especifica un TAD que se puede expresar en Maude como se describe a continuación.
4.1 TAD asociado con una relación del DC
El nombre de una relación (o los nombres de las clases relacionadas separados por “-”), hace referencia a un TAD que contiene todas las posibles parejas que se pueden formar con las instancias de las clases relacionadas. Para el caso de estudio estos TADs son los siguientes:
sort usuario-album.
sort album-imagen.
4.2 Constructor asociado con una relación del DC
Las posibles instancias de una relación son todas las posibles parejas que se pueden formar con instancias de las clases relacionadas, considerando que el primer elemento de la pareja debe ser instancia de una de las dos clases y el segundo elemento debe ser instancia de la otra. Para representar dichas parejas la formalización provee un operador constructor. Así, para el caso de estudio el constructor para la relación entre usuario y álbum es:
op usuario-album<_,_> : Usuario Album -> usuario-album . [ctor].
Nótese que el constructor básicamente expresa que el TAD asociado con la relación es el producto cartesiano de los TADs de las clases relacionadas.
Para el caso de la relación album-imagen, el constructor contiene también el atributo que registra el número de orden (numeroOrden en el DC de la Figura 1) de la imagen en el álbum, así:
op album-imagen<_,_,_> :
Album Imagen Int -> album-imagen . [ctor].
Por medio del constructor es posible referirse a cualquiera de las instancias de la relación. Así, son nstancias de las relaciones del ejemplo, los siguientes términos:
Ejemplos
usuario-album< usuario<persona<1,"Joe">,"Joe el Malo","AvtJoe.jpg">,
album<"Perú","Inca">
>.
album-imagen< album<"Perú","Inca">
imagen<"faro.jpg","Faro en el fin del mundo", "El Faro","Sin comentarios">,
23
>.
4.3 Selectores con notación punto para los TADs asociados con las relaciones
Al igual que para la clase, el TAD asociado con las relaciones posee operadores selectores con notación punto que tienen como dominio el TAD asociado con la relación y como rango el TAD asociado con las clases relacionadas.
Para estos selectores, el nombre luego del punto será el nombre del rol correspondiente al lado de la clase relacionada o el nombre de la clase relacionada. Para el caso de estudio, son selectores los siguientes:
op _.album : album-imagen -> Album. op _.imagen : album-imagen -> String.
vars Alb : Album. vars Img : String. vars NoOrden : Int.
eq album-imagen<Alb,Img,NoOrden>.album = Alb.
eq album-imagen<Alb,Img,NoOrden>.imagen = Img.
Ejemplo
album-imagen<
album<"Perú","Inca">, imagen<"faro.jpg","Faro en el fin del mundo","El Faro","Sin comentarios">, 23>.album
= album<"Perú","Inca">.
Para la relación album-imagen, la formalización provee también un selector para obtener el atributo (numeroOrden) propio de la relación, así:
op _.numeroOrden : album-imagen
-> Int.
eq album-imagen<Alb,Img,NoOrden
>.numeroOrden = NoOrden.
Ejemplo
album-imagen< album<"Perú","Inca">,
imagen<"faro.jpg","Faro en el fin del mundo","El Faro","Sin comentarios">, 23>.numeroOrden
= 23.
5. TAD ASOCIADO CON LA EXTENSIÓN DE LAS CLASES Y LAS RELACIONES
La BD contiene un conjunto de instancias para cada una de las clases y relaciones de la especificación. Al conjunto de instancias almacenadas en la BD, se le ha denominado la “extensión” de la clase (o de la relación).
Para las extensiones, la formalización propuesta extiende la especificación en Maude de conjuntos genéricos presentada en [34] (sección 7.12.25), con operadores sobre conjuntos y con los TAD asociados con las extensiones.
5.1 Selectores con notación punto aplicados sobre conjuntos de clases y relaciones
El operador punto definido para las clases y relaciones se puede extender para conjuntos reusando las definiciones anteriores. Así, en la formalización propuesta la evocación del operador sobre un conjunto hará referencia al conjunto que contiene el resultado de la evocación del mismo operador sobre cada uno de los elementos del conjunto inicial.
Para el caso de estudio, se muestran a continuación algunos de estos operadores:
op _.nombre : Set{Album}
-> Set{String}.
op _.descripcion : Set{Album}
-> Set{String}.
Ejemplos
{album<"Perú","Inca">, album<"Australia","Su gran desiert >
}.nombre
= {album<
"Perú","Inca">.nombre, album<
"Australia","Su gran desierto">.nombre
}
= {"Perú","Australia"}
Nótese que la definición anterior es válida tanto para conjuntos de clases como para conjuntos de relaciones.
var P : PreSetAlbum.
var E : ElementAlbum.
var A : Album.
eq {}.nombre = {}.
eq {A}.nombre = {A.nombre}.
eq (E, P).nombre =
union((E.nombre),(P.nombre)).
5.2 TAD asociado con las extensiones
La formalización propuesta provee un TAD específico para las extensiones de cada clase y relación. El TAD asociado con la extensión de una clase o relación, contiene todos los posibles conjuntos de instancias de dicha clase o relación que puedan estar contenidos en la BD. En el caso de estudio la formalización provee los siguientes TADs para las extensiones de las clases:
sort usuario_s.
sort album_s.
sort imagen_s.
Y provee los siguientes TADs para para las extensiones de las relaciones:
Son ejemplos de instancias de dichos TADs los siguientes:
usuario_s< usuario<persona<1,"Joe">,"Joe el
Malo","AvtJoe.jpg">,
usuario<persona<2,"Mario">,"Mario el
Grande","AvtMario.jpg">
>
imagen_s< imagen<"faro.jpg","Faro en el fin
del mundo","El Faro","Sin comentarios">
imagen<"pig.jpg","Cerdo doméstico","El
Cerdo","Sin comentarios">,
imagen<"horse.jpg","Caballo
doméstico","El Caballo","Sin
comentarios">
5.3 Restricciones sobre las extensiones
Las extensiones de las clases y relaciones deben cumplir con las restricciones que para ellas especifique el DC.
Para ello se usa la ecuación de membresía condicional de Maude de la forma descrita en [34] (secciones 4.2 y 4.3). La formalización considera primero, que los TADs asociados con las extensiones son subtipos de los conjuntos potencia de los TADs asociados con las clases y relaciones correspondientes, así:
subsort usuario_s < Set{Usuario}.
subsort album_s < Set{Album}.
subsort imagen_s < Set{Imagen}.
subsort usr-alb_s < Set{usuario-album}.
subsort alb-img_s < Set{album-imagen}.
Luego, la formalización indica por medio de ecuaciones de membresía y de membresía condicional, que un conjunto cualquiera de instancias de una clase o relación, pertenece al TAD de la extensión que le corresponde, solo si cumple con las restricciones que se le impone al DC.
Para el caso de estudio la restricción unique indica que la cédula de un usuario, solo puede aparecer una vez en la extensión de la clase Persona, así:
vars P1 P2 : Persona.
var EXT_P : Set{Persona}.
cmb EXT_U : persona_s
if(((P1 in EXT_P) and
(P2 in EXT_P) and
(P1 =/= P2))
implies (P1.cedula =/= P2.cedula )).
Donde
=/= representa el símbolo diferente de (![]() ).
).
Las cardinalidades de los roles en una relación, por su parte, limitan el número de veces que puede aparecer una instancia de la clase asociada al rol en la extensión de la relación. Para el caso particular de la cardinalidad sobre el rol “pertenece” en el DC que indica que un álbum solo se relaciona con un usuario, la ecuación de membresía condicional es la siguiente:
var UA1 UA2 : usuario-album.
cmbEXT_UA : usr-alb_s if((
(UA1 in EXT_UA) and
(UA2 in EXT_UA) and
(UA1.tiene == UA2.tiene)) implies
(UA1 == UA2)).
6. TAD ASOCIADO CON EL DC
El DC como un “todo”, especifica un TAD que se puede expresar en Maude como se describe a continuación:
6.1 Sort asociado con el DC
El nombre del DC hace referencia a un TAD que contiene todas las posibles BDs que satisfagan la especificación. Para el caso de estudio:
sort album_de_imagenes.
6.2 Constructor del TAD asociado con el DC
Las posibles instancias del DC son tuplas formadas con extensiones de las clases y de las relaciones definidas en el DC. Para representar una de dichas instancias en el caso de estudio, se define en Maude el siguiente operador constructor:
subsort album_de_imagenes <
album_de_imagenes.
op adei<_,_,_,_,_> :
usuario_s
album_s
imagen_s
usr-alb_s
alb-img_s
-> album_de_imagenes . [ctor].
Nótese que el constructor básicamente expresa que los elementos del TAD asociado con el DC son todas las posibles combinaciones válidas de extensiones de las clases y de las relaciones.
Ejemplo
op ADEI : -> album_de_imagenes.
eq ADEI = adei<
{usuario<persona<1,"Joe">,"Joe el
Malo","AvtJoe.jpg">,
usuario<persona<2,"Mario">,"Mario el
Grande","AvtMario.jpg">
},
{album<"Naturaleza","Amazonas">,
album<"Perú","Inca">,
album<"India","Calor Extremo">
},
{
imagen<"faro.jpg","Faro en el fin del mundo","El
Faro","Sin comentarios">
imagen<"pig.jpg","Cerdo doméstico","El
Cerdo","Sin comentarios">,
imagen<"horse.jpg","Caballo doméstico","El
Caballo","Sin comentarios">
},
{
usuario-album
<usuario
<persona<1,"Joe">,"Joe el Malo","AvtJoe.jpg">,
album<"Perú","Inca">
>,
usuario-album
<usuario
<persona<2,"Mario">,"Mario el
47
Grande","AvtMario.jpg">,
album<"India","Calor Extremo">
>
},
{
usuario-imagen
<usuario<persona<1,"Joe">,"Joe el
Malo","AvtJoe.jpg">,
imagen<"horse.jpg","Caballo doméstico","El
Caballo","Sin comentarios">
>
},
{
album-imagen
<album<"Perú","Inca">,
imagen<"faro.jpg","Faro en el fin del mundo","El
Faro","Sin comentarios">,
23
>
}>
En el ejemplo anterior se usa el nombre abreviado del TAD de la BD en mayúscula (ADEI) para referirse a la instancia de la BD.
6.3 Selectores con notación punto para los TADs asociados con el DC
Al igual que para la clases y las relaciones, el TAD
asociado con el DC posee operadores selectores
con notación punto, que tienen como dominio el
TAD asociado con el DC y como rango el TAD
asociado con cada uno de las extensiones
componentes:
op _.album : album_de_imagenes ->
album_s.
op _.imagen : album_de_imagenes ->
imagen_s.
op _.album-imagen: album_de_imagenes -
>alb-img_s.
Ejemplo
adei<
{usuario<persona<1,"Joe">,"Joe el
Malo","AvtJoe.jpg">,
usuario<persona<2,"Mario">,"Mario el
Grande","AvtMario.jpg">
},
{album<"Naturaleza","Amazonas">,
album<"Perú","Inca">,
album<"India","Calor Extremo"> },
{
}>.album =
{album<"Naturaleza","Amazonas">,
album<"Perú","Inca">,
album<"India","Calor Extremo">
}
Para simplificar la especificación de operadores que se relacionen con las extensiones de una BD se usará en lo que sigue el nombre del TAD abstracto asociado con la extensión en mayúscula como subrogado de la extensión.
Esto equivale a definir en Maude una serie de operadores de aridad 0 para cada una de dichas extensiones. Para la extensión de la clase usuario, en el caso de estudio, el operador correspondiente es el siguiente:
op USUARIO : -> usuario_s.
eq USUARIO = ADEI.usuario.
6.4 Restricciones asociadas con el DC
A pesar de que el constructor definido para el TAD asociado con la BD, captura la estructura básica de las BDs que el DC representa, se queda corto en relación con las restricciones globales que impone el DC.
Para capturar estas restricciones en el TAD asociado con el DC, se usará de nuevo la ecuación de membresía condicional de Maude. El primer paso para usar esta ecuación, fue dado al considerar que el TAD asociado con las instancias del DC (album_de_imágenes) es subtipo del TAD asociado como codominio del constructor (album_de_imagenes); en otras palabras, no todos los términos del constructor son instancias correctas del DC.
Luego por medio de una ecuación de membresía condicional, se indicará cuando una instancia del constructor (miembro de album_de_imagenes) pertenece al TAD de las instancias correctas del DC (album_de_imagenes).
La primera restricción sobre las instancias de album_de_imagenes es que los objetos que aparezcan en una relación, deben aparecer también en la extensión de sus respectivas clases.
vars U : Usuario.
vars ADI : album_de_imagenes.
cmb ADI : album_de_imagenes
if((U in ADI.usuario-album.usuario) implies
(U in ADI.usuario).
6.5 Selectores con notación punto asociados con los roles en las relaciones
Los lenguajes OO ofrecen también la notación [objeto].[rol], para referirse a los objetos con los que se relaciona un objeto a través de la relación que posee el rol. Para ello la formalización define, en el TAD de las extensiones de cada clase, selectores de notación punto para los roles que le competan. Para el caso de estudio dentro del conjunto de selectores están los siguientes:
Ejemplo
Dada la extensión de la relación usuario-album
usuario-album = {
usuario-album<
usuario<persona<1,"Joe">,"Joe el
Malo","AvtJoe.jpg">,
album<"Perú","Inca">
>,
usuario-album<
usuario<persona<2,"Mario">,"Mario el
Grande","AvtMario.jpg">,
album<"Cumple","2013">
usuario-album<
usuario<persona<1,"Joe">,"Joe el
Malo","AvtJoe.jpg">,
album<"Familia","1988">
>
Se tiene que:
usuario<
persona<1,"Joe">,"Joe el Malo","AvtJoe.jpg"
>.tieneAlbum
= {album<"Perú","Inca">,
album<"Familia","1988">}
La definición en Maude de este operador es la
siguiente:
op _.tieneAlbum : Usuario -> Set{Album}.
vars U1 U2 : Usuario.
eq U1.tieneAlbum =
{X: USUARIO-ALBUM /X.usuario == U1
}.album.
Donde se usaron operadores de selección sobre conjuntos de la forma {X: <set>/ C(x)} de la forma definida en [35].
7. EL SIGNIFICADO DE LA HERENCIA
En la formalización propuesta, la herencia entre clases tiene como objetivo principal permitir que las clases descendientes extiendan las propiedades de las clases que constituyen sus ancestros, manteniendo la identidad de tipo (i.e., que un un objeto de una clase “descendiente” pueda ser considerado también como un objeto de la clase “ancestro”). Esta forma de extensión es equivalente a tener en los objetos de las clases “hijas” un objeto embebido de la clase “padre”.
Para ello, la formalización le da semántica a la herencia a través de los elementos que se describen a continuación.
7.1 La inclusión de los atributos de lasclases ancestro en las clases descendiente
Un aspecto esencial en la herencia es el de incluir los atributos de las clases ancestro en las clases descendientes. En la formalización propuesta esto se interpreta como la inclusión en las clases descendientes de una instancia de su ancestro más inmediato.
Para el caso de estudio la relación de herencia
entre Usuario y Persona se interpreta así:
sort Usuario.
op Usuario<_,_,_> :
Persona String String . [ctor].
Nótese que la semántica del constructor sigue
siendo la misma: representar la clase como el
producto cartesiano del TAD de sus atributos.
Ejemplos
usuario<persona<1,"Joe">,"Joe el
Malo","AvtJoe.jpg">.
usuario<persona<2,"Mario">,"Mario el
Grande","AvtMario.jpg">
7.2 Herencia de selectores
Por ser los atributos de los ancestros, también atributos de sus descendientes, estos últimos deben contar con selectores idénticos a los de sus ancestros. En la formalización propuesta esto se traduce en que los selectores de la clase hija, correspondientes a los selectores de la clase padre, transfieren el operador al objeto de la clase padre embebido. En otras palabras, la clase hija tendrá Revista Politécnica ISSN 1900-2351 (Impreso), ISSN 2256-5353 (En línea), Año 12, Número 23, páginas 39-50, Julio – Diciembre 2016 49 visibilidad de los atributos de la clase padre a través de la transferencia del operador de selección al objeto padre embebido, así:
Si los operadores de persona son los siguientes
op _.nombre : Persona -> string.
vars Nom : String.
vars Ced : String.
eq Persona<Ced,Nom>.nombre
= Nom.
Y se declara el TAD Usuario así
sort Usuario.
op Usuario<_,_,_> :
Persona String String . [ctor].
Entonces la herencia de operadores se entiende así
vars P : Persona.
vars Avatar : String.
vars Nick : String.
eq Usuario<P,Nick,Avatar>.nombre = P.nombre.
Es decir, el nombre del usuario es el nombre de P (Persona). Se debe considerar además posibles restricciones, e.g., evitar que una clase hija tenga un atributo con igual nombre al de un atributo de la clase padre. De lo contrario, habría una ambigüedad al invocar al selector nombre en Usuario.
8. CONCLUSIÓN Y TRABAJOS FUTUROS
En este trabajo se propuso una especificación formal mediante el lenguaje Maude para el DC. La especificación propuesta evita ambigüedades y además facilita la representación a nivel de instancia de la BD asociada con el DC y no solo de la parte estructural.
Como trabajos futuros se proponen los siguientes: i) extender la formalización para la inclusión de métodos, i.e., formalizar la parte del comportamiento, ii) formalizar de manera similar otros diagramas de UML y iii) aplicar una técnica de formalización similar a otros paradigmas de desarrollo.
9. AGRADECIMIENTOS
Los autores deseas expresar sus agradecimientos al profesor Paulino José García Nieto de la Universidad de Oviedo por sus valiosos comentarios y ayuda en la formalización con el lenguaje Maude.
10. REFERENCIAS BIBLIOGRÁFICAS
[1] G. Booch, R. Maksimchuk, M. Engle, J. Conallen, K. Houston, and J. Bobbi, Object oriented design with applications. Redwood City, USA, 1991.
[2] J. Rumbaugh, M. Blaha, W. Premerlani, and F. Eddy, Object-oriented modeling and design. Prentice-hall, 1991.
[3] I. Jacobson, “Object Oriented Software Engineering: A Use Case Driven Approach,” 1992.
[4] B. Meyer, Object-oriented software construction, Vol 2. New York, USA: Prentice hall, 1988.
[5] G. Booch, I. Jacobson, and J. Rumbaugh, “OMG Unified Modeling Lenguage Specification,” 2000. [Online]. Available: http://www.omg.org/spec/UML/. [Accessed: 20-Apr-2016].
[6] F. Arango Isaza, Aplicaciones de la Lógica al Desarrollo de Software: Lenguajes Lógicos y Funcionales (sec 4.3), 2nd ed. Medellín, Colombia: Universidad Nacional de Colombia, 2016.
[7] B. Rumpe, “A Note on Semantics (with an Emphasis on UML),” Second ECOOP Work. Precise Behav. Semant., 1998.
[8] J. Warmer and A. Kleppe, “The Object Constraint Language: Precise Modeling With Uml (Addison-Wesley Object Technology Series),” 1998.
[9] J. Fitzgerald, P. Larsen, P. Mukherjee, and N. Plat, Validated designs for object-oriented systems. 2005.
[10] C. B. Jones, Systematic software development using VDM. Prentice Hall, 1990.
[11] A. Evans, R. France, K. Lano, and B. Rumpe, “Developing the UML as a formal modelling notation,” UML’98 Beyond notation. Int. Work. Mulhouse Fr., 1998.
[12] A. Evans, “Reasoning with UML class diagrams,” , 1998. Proceedings. 2nd IEEE Work., 1998. Revista Politécnica ISSN 1900-2351 (Impreso), ISSN 2256-5353 (En línea), Año 12, Número 23, páginas 39-50, Julio – Diciembre 2016 50
[13] A. Evans and S. Kent, “Core meta-modelling semantics of UML: the pUML approach,” Int. Conf. Unified Model., 1999.
[14] A. Hall, “Specifying and interpreting class hierarchies in Z,” Z User Work. Cambridge 1994, 1994.
[15] M. Cengarle, H. Grönninger, and B. Rumpe, “System model semantics of class diagrams,” arXiv Prepr., 2008.
[16] N. Zafar and F. Alhumaidan, “Transformation of class diagrams into formal specification,” Int. J. Comput. Sci., 2011.
[17] J. Woodcock and J. Davies, Using Z: specification, refinement, and proof. Prentice hall, 1996.
[18] D. Berardi, D. Calvanese, and G. De Giacomo, “Reasoning on UML class diagrams,” Artif. Intell., 2005.
[19] L. Efrizoni and W. Wan-Kadir, “Formalization of UML class diagram using description logics,” 2010 Int. Symp. Inf. Technol., vol. 3, 2010.
[20] F. Baader, The description logic handbook: Theory, implementation and applications. 2003.
[21] H. Ledang, “Automatic translation from UML specifications to B,” Autom. Softw. Eng. 2001.(ASE 2001), 2001.
[22] H. Ledang, “Formal techniques in the bjectoriented software development: an approach based on the B method,” 11th PhDOOS ECOOP2001 Dr. Work., 2001.
[23] C. Snook and M. Butler, “UML-B: Formal modeling and design aided by UML,” ACM Trans. Softw. Eng., 2006.
[24] A. T. Álvarez and J. L. Alemán, “Formally modeling UML and its evolution: a holistic approach,” Form. Methods Open ObjectBased Distrib. Syst. IV, vol. 49, 2000.
[25] N. Bourbaki, “Theory of sets,” Springer Berlin Heidelb., pp. 65–129, 2004. [26] A. Hall, “Using Z as a specification calculus for object-oriented systems,” Int. Symp. VDM Eur., 1990.
[27] R. H. Bourdeau and B. H. C. Cheng, “A formal semantics for object model diagrams,” IEEE Trans. Softw. Eng., vol. 21, no. 10, pp. 799–821, 1995.
[28] J. Guttag, J. Horning, S. J. Garland, K. D. Jones, A. Modet, and J. M. Wing, Larch: languages and tools for formal specification. 1993.
[29] M. Clavel, F. Durán, S. Eker, P. Lincoln, N. Martı́ -Oliet, J. Meseguer, and J. F. Quesada, “Maude: specification and programming in rewriting logic,” Theor. Comput. Sci., vol. 285, no. 2, pp. 187–243, 2002.
[30] J. Guttag, “Abstract Data Types and the Development of Data Structures,” in Software Pioneers, Berlin, Heidelberg: Springer Berlin Heidelberg, 2002, pp. 453– 479.
[31] S. Clérici, R. Jiménez, and F. Orejas, “Classsort polymorphism in GLIDER,” in Recent Trends in Data Type Specification, Springer Berlin Heidelberg, 1996, pp. 143–160.
[32] F. Baader and T. Nipkow, Term rewriting and all that. Cambridge University Press, 1999.
[33] D. A. Plaisted, “Equational reasoning and term rewriting systems,” in Handbook of logic in artificial intelligence and logic programming (vol. 1), New York, NY, USA: Oxford University Press, 1998, pp. 274–364.
[34] M. Clavel, F. Durán, S. Eker, P. Lincoln, N. Martí-Oliet, J. Meseguer, and C. Talcott, All About Maude - A High-Performance Logical Framework: How to Specify, Program, and Verify Systems in Rewriting Logic, vol. 4350. Berlin, Heidelberg: Springer Berlin Heidelberg, 2007
.
[35] M. Clavel, F. Durán, S. Eker, P. Lincoln, N. Martí-oliet, J. Meseguer, and C. Talcott, “Maude Manual (Version 2.5),” 2010.