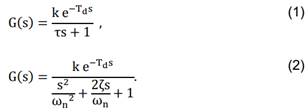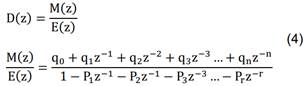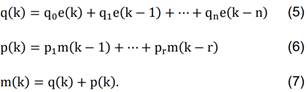APLICACIÓN
DE DISEÑO, SIMULACIÓN, IDENTIFICACIÓN DE SISTEMAS E IMPLEMENTACIÓN DE
CONTROLADORES PID - DIGITROL
Jhon Alexander Ramírez Urrego1,
Norha Ligia Posada Restrepo2
.
1Ingeniero en
Instrumentación y Control. Especialista en Gerencia de Mantenimiento
Universidad de Antioquia. Profesional del área de Ambiente Físico y Medio
Ambiente del E.S.E. Hospital Manuel Uribe Ángel, Diagonal 31 36ª sur 80,
Envigado-Colombia. Correo electrónico: jhon_ramirez91081@elpoli.edu.co.
2Magíster en
Ingeniería de la Universidad Pontificia Bolivariana, Especialista en Automática
de la Universidad Pontificia Bolivariana, Ingeniera en Instrumentación y
Control. Docente de la Universidad Pontificia Bolivariana, Facultad de
Ingeniería Mecánica. Correo electrónico: norha.posada@upb.edu.co
RESUMEN
Se presentan dos herramientas digitales para el ajuste,
diseño, simulación e implementación de controladores PID, con las cuales se pueden
adquirir los datos, obtener el modelo matemático que describe el comportamiento
de la planta, y el controlador a implementar en el proceso real. Las
herramientas fueron elaboradas con software de uso común en los sistemas de
control. Para la identificación, diseño y simulación del controlador se usó
Matlab® y para la adquisición de datos y la implementación se trabajó con
LabVIEWTM. Se obtuvieron datos de una planta didáctica y se ajustó un
controlador por ganancia última. En la simulación se evidenció un alto esfuerzo
de control sobre el elemento final de control (EFC), debido a esto se
ponderaron los parámetros obtenidos en el ajuste del controlador, evidenciando
así la utilidad de la simulación de los sistemas de control antes de la
implementación.
Palabras
clave: Diseño
y ajuste de controladores PID, Modelado matemático de procesos, simulación de sistemas
controlados, implementación de controladores PID
Recibido:
5 de Julio de 2016. Aceptado: 28 de Diciembre de 2016
Received:
July 5th, 2016. Accepted: December 28th, 2016
APPLICATION
FOR DESIGN, SIMULATION, SYSTEM IDENTIFICATION AND IMPLEMENTATION OF PID
CONTROLLERS
- DIGITROL
ABSTRACT
Two
computational tools for tuning, design, simulation and implementation of PID
controllers are presented. These allow data acquisition, system identification,
setting and implementation controllers in the real process. The tools were
developed with software commonly used in control systems. For identification,
controller design and simulation Matlab® was used and for data acquisition and
implementation was worked with LabVIEWTM. Data were obtained from a didactic
plant and controller was tuned for the Ultimate Gain. In the simulation
evidenced a high effort of control over the valve was evident, so in
implementing the controller parameters were weighted, in order to improve the
valve performance, thus showing the utility of the control system simulation
before implementation.
Keywords: Design and adjustment
of PID controllers, process Mathematical modeling, simulation of
controlled
systems, implementation of PID controllers
Cómo
citar este artículo:
J. A. Ramírez y N.L. Posada, “Aplicación de diseño, simulación, identificación
de sistemas e implementación de controladores PID - Digitrol” Revista
Politécnica, vol. 12, no. 23, pp. 17-25, 2016.
1.
INTRODUCCIÓN
Los
algoritmos de control tipo PID (Proporcional, Integral Derivativo) son de los
más utilizados en la industria, por ser versátiles, ya que se puede configurar
como un P, PI, PD o PID; sencillos y fáciles de implementar tanto en
controladores industriales, PLC (Programmable Logic Controller) como en
computadores. Sumado a esto en la literatura se encuentran varias metodologías
de ajuste y diseño que permiten obtener sus parámetros con un mínimo de
conocimiento en control [1], [2].
Para
el diseño y análisis del comportamiento de los controladores se usa,
generalmente, un programa de computador que permite realizar la simulación de
su comportamiento, evitando así los costos y los tiempos de paro que generaría
el implementarlos y probarlos directamente en un proceso real. Es así como en
ingeniería de control se utilizan software como Matlab®, LabViewTM, Scilab,
Octave, Control Station y Excel, entre otros que facilitan el diseño de
sistemas de control, que van desde los convencionales hasta los avanzados, y la
simulación de los mismos mediante herramientas de programación que entregan
resultados gráficos y numéricos, con base en los cuales se analizan las bondades
de los controladores a implementar y se selecciona el más adecuado de acuerdo a
las condiciones, necesidades y exigencias reales del proceso [3]. Es de aclarar
que muchos de los ambientes de simulación son transparentes en cuanto a su
codificación. En general las funciones usadas en estos programas requieren de
pocos parámetros para su configuración. Luego de ingresar los argumentos a las
funciones, estas producen diversos resultados numéricos y gráficos por medio de
ventanas emergentes. El cómo se generó y cuál es la estructura algorítmica
usada es irrelevante, prestando atención solo al conjunto de eventos visuales
resultantes.
El
diseño y simulación de sistemas en la ingeniería de control se puede llevar a
cabo mediante dos metodologías. La primera consiste en modelar matemáticamente
el proceso, una alternativa relacionada con la modelación matemática es la identificación
del sistema mediante técnicas experimentales, que permiten la obtención de un modelo,
normalmente, de orden reducido: Primer Orden con Retardo (POR) o Segundo Orden
con Retardo (SOR). Modelos que son necesarios para la sintonización de
controladores en lazos retroalimentados [4]. La segunda utiliza aplicaciones
orientadas que incluyen elementos predefinidos asociados, por ejemplo,
componentes eléctricos, mecánicos, controladores et al [5].
La
simulación se considera como una herramienta útil para demostrar, analizar y
experimentar con los sistemas de control que se pueden encontrar en la industria.
Así como para aplicar las teorías que se trabajen en cursos de Ingeniería de
Control y que por razones de costo, tiempo o disponibilidad de la planta no se
pueden probar directamente en el proceso. Mediante la simulación se puede hacer
una buena aproximación a la dinámica real de los procesos. En la literatura se
encuentran reportados ejemplo de aplicaciones dirigidas a la simulación de sistemas
como son: el seguimiento de energía solar mediante el control del ángulo de un
panel solar [6], simuladores para el control de aeronaves [7], y otras para el
diseño basado en simulación de estrategias de control aplicadas a las plantas
de tratamiento de aguas residuales [8]. En algunos trabajos resaltan la
importancia de la simulación para la disminución del tiempo de diseño en la
fase experimental [9], mientras que otros muestran tendencias hacia
laboratorios virtuales para los cuales desarrollan aplicaciones que permiten la
simulación de controladores aplicados sobre procesos de forma remota [10],
[11]. Mediante la simulación se pueden comparar diversas estrategias de control
clásicas y avanzadas. La comparación permite evaluar el desempeño del sistema
bajo criterios de estabilidad y robustez en diversos modelos de plantas de
procesos [12].
En
general, contar con una aplicación de software en la que se pueda simular el
diseño y con la información obtenida realizar la implementación, permitirá el
paso de la teoría al comportamiento real. Las bondades de esto se evidencia en
casos como los de la acción derivativa de un PID, la cual es usual que
amplifique el ruido en el sistema de control. En la práctica esto podría llegar
a causar daño en el elemento final de control y es una de las razones por las
cuales se recomienda la simulación del sistema controlado antes de la
implementación [13].
En
este trabajo se muestra el resultado del desarrollo de herramientas
computacionales para el diseño, análisis, identificación, simulación e implementación
de sistemas de control en tiempo discreto. La herramienta pretende demostrar la
capacidad que brinda la programación de
algoritmos
en ingeniería y la necesidad de comprender desde los ámbitos de estudio del control
de procesos la importancia de la estrategia PID [14]. En el artículo se
muestran las etapas de desarrollo partiendo desde la adquisición o generación
de la base de datos, identificación del sistema, discretización, análisis de
estabilidad, ajuste y simulación de controladores hasta la implementación con
los resultados dados por la simulación. Estos últimos aplicados en una planta didáctica
a escala de un proceso industrial.
2. MATERIALES
Y METODO
Las herramientas que se presentan permiten, a estudiantes y
docentes de control digital, e identificación de sistemas la modelación y el análisis
de sistemas, así como el ajuste, el diseño, la simulación y la implementación
de controladores en procesos reales.
Para el diseño de la aplicación se tuvieron en cuenta
requerimientos relacionados con el diseño de sistemas de control PID en tiempo
discreto. Estos requerimientos fueron: generación de datos a partir de un
modelo matemático o adquisición de datos de un proceso real, identificación del
sistema (obtención del modelo matemático como una aproximación POR o SOR),
discretización del modelo, análisis de estabilidad, ajuste de controladores,
obtención de los parámetros del controlador y finalmente la implementación del controlador
ajustado o diseñado. La aplicación fue dividida en dos módulos, en el primero
de ellos se desarrolló la etapa de diseño, simulación y generación de
resultados. En el segundo modulo se desarrolló la etapa de adquisición de datos
y de implementación.
El primer módulo fue desarrollado en Matlab® [15] bajo una
estructura modular con funciones independientes entre los bloques de
programación. Lo anterior facilitó la adición y depuración de código en todo el
diseño. Se eligió Matlab® debido a su potente entorno gráfico, capacidad de
cálculos complejos y en especial por su importante contribución académica en el
estudio de sistemas de control [16]. El segundo módulo fue desarrollado en
LabVIEWTM conservando la estructura modular en la programación. Se eligió esta
plataforma debido a su flexibilidad para conectarse con sistemas hardware [17].
A continuación se presenta la descripción general de la aplicación.
2.1 Software para ajuste y simulación de controladores
PID
El primer módulo de la aplicación fue denominado DIGITROLM.
Éste permite la identificación del sistema, el ajuste de controladores
convencionales digitales y su simulación, en general es un aplicativo de fácil
manejo basado en interfaces amigables con el usuario, encargadas de dirigirlo a
través de una secuencia de interfaces independientes que inician con la lectura
o generación de bases de datos, identificación, selección del tiempo de
muestreo, discretización, análisis de estabilidad, hasta permitir el ajuste y
la simulación de controladores PID.
Se decidió trabajar mediante el llamado a funciones a
partir de un único archivo de cabecera el cual contiene la programación de los
objetos que estructuran el entorno de trabajo y el llamado a las subfunciones
para cada paso en la secuencia.
Inicialmente se presenta el about de la aplicación (Fig. 1)
y se sigue con la presentación de la secuencia de trabajo mediante botones de
acción. Estos botones fueron ordenados como si se tratara de un diagrama de
flujo para el diseño de sistemas de control, y en una nueva ventana como se muestra
en la Fig. 2. Las opciones se deshabilitan dejando a disposición del usuario el
paso correspondiente en la secuencia de diseño.

Fig.1.About:
Presentación inicial de la aplicación, DIGITROLM
Fig. 2. Ventana con la
secuencia de trabajo de la aplicación DIGITROLM
2.1.1 Base de Datos:
Es el primer paso en el diseño del sistema de control (Fig. 3). En este se presentan,
al usuario, dos opciones: la primera de ellas permite el ingreso de un modelo
POR o SOR para generar una base de datos con la respuesta del modelo ante
estímulos tipo escalón y de la magnitud deseada y la segunda, permite cargar una
base de datos adquirida de un proceso, la cual debe estar ordenada en tres
columnas (tiempo, respuesta del sistema, y magnitud del escalón). Ambas
opciones presentan en una ventana emergente la gráfica de los datos.
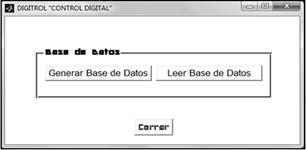
Fig.3. Opciones generar
base de datos y leer base de datos, aplicación DIGITROLM
La aplicación preguntará sobre el estado de la base de
datos con dos posibles opciones, la primera si se encuentra en unidades de
voltaje (0 a 5 VDC) y la segunda si fue generada en porcentaje (0 a 100%),
ambas opciones con relación al eje (y) y previamente validadas, es decir que
las unidades deben de ajustarse al eje, de lo contrario la aplicación le
indicará que los datos no coinciden y que debe de realizar una inspección de su
base de datos en razón a sus unidades.
2.1.2 Identificación del sistema:
Una de las formas de modelar la dinámica de un sistema es mediante la
aplicación de estímulos en su entrada. Entre estos métodos se encuentra la
aproximación de la respuesta del sistema cuando se aplica un estímulo de tipo
escalón. La aproximación puede dar como resultado sistemas POR o SOR. El sistema
POR es caracterizado por tres parámetros: ganancia (K),
constante de tiempo (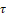 ) y tiempo de retardo (Td),
como se muestra en la ecuación (1), este modelo es usado para sintonización de controladores
convencionales, por ejemplo las tablas de ajuste dadas por Ziegler-Nichols [2],
[18]. El modelo SOR es caracterizado por cuatro parámetros: ganancia (k),
frecuencia natural (ωn),
factor de amortiguamiento (ߞ
) y tiempo de retardo (Td),
como se muestra en la ecuación (2) [19].
) y tiempo de retardo (Td),
como se muestra en la ecuación (1), este modelo es usado para sintonización de controladores
convencionales, por ejemplo las tablas de ajuste dadas por Ziegler-Nichols [2],
[18]. El modelo SOR es caracterizado por cuatro parámetros: ganancia (k),
frecuencia natural (ωn),
factor de amortiguamiento (ߞ
) y tiempo de retardo (Td),
como se muestra en la ecuación (2) [19].
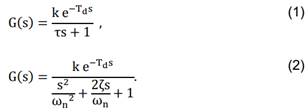
En la Figura 4 se muestra la interface que permite la
selección del modelo a obtener, ambas identificaciones corresponden al método
no paramétrico de Cecil Smith, [20].
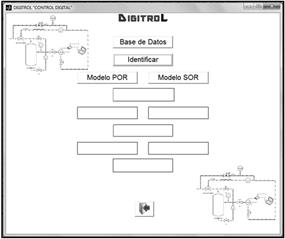
Fig.4. Opciones de
Identificación; aplicación DIGITROLM
La Fig. 5 muestra los valores numéricos obtenidos para la
función de transferencia del sistema en TextBox y la respuesta gráfica del
modelo y el escalón con el que se hace la simulación
2.1.3 Período de muestreo:
El diseño de sistemas de control digitales requiere la obtención del modelo en
función del tiempo discreto. Este modelo es obtenido a partir de un proceso
denominado
digitalización en el cual el modelo dado por (1) o (2) es
llevado a una función en términos de Z. El primer paso en la digitalización es
determinar el período de muestreo adecuado, el cual permite establecer la
relación que existirá entre la variable el sistema en tiempo continuo y en el
dominio del dominio del tiempo discreto [21].
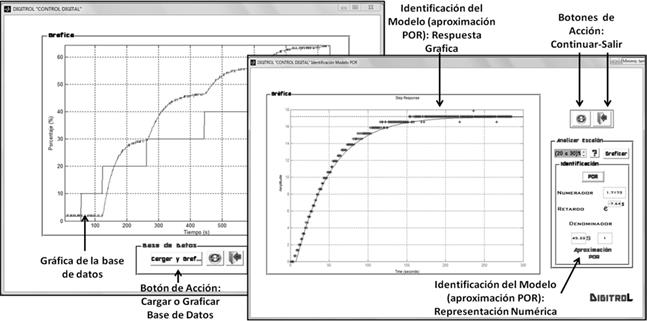
Fig.5. Interface de las
opciones: base de datos e identificación del sistema; aplicación DIGITROLM
DIGITROLM permite elegir el período de muestreo de los
valores obtenidos por dos métodos: el criterio de ancho de banda y el criterio
de la constante de tiempo equivalente del sistema. Además, la aplicación cuenta
con rutinas de ayuda y validación. Por ejemplo, en el caso del período de muestreo
se evalúa el valor ingresado por el usuario, de manera que dicho valor esté comprendido
en el intervalo calculado de acuerdo al criterio usado (Fig. 6).
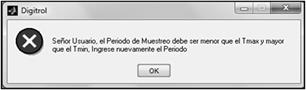
Fig.6. Validación del
período de muestreo; aplicación DIGITROLM
La visualización del sistema discretizado es opcional, no
es un paso necesario para continuar con el diseño y ajuste de los
controladores, validado el período de muestreo un cuadro de dialogo presentará
la posibilidad de observar el sistema digitalizado. La Fig. 7 muestra la
interfaz con la respuesta del sistema en tiempo continuo y discreto ante una
entrada tipo escalón con su respectiva función de transferencia en el dominio de
Laplace y de la transformada (Z) y el período de muestreo seleccionado. El
resultado gráfico en esta interface permitirá determinar si el modelo continuo corresponde
al modelo discreto. La función de transferencia en dominio de (z) tiene la
forma indicada en (3).
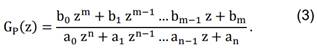
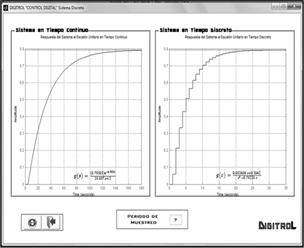
Fig. 7. Interface del
Sistema en tiempo continuo y discreto, aplicación DIGITROLM.
2.1.4 Estabilidad:
A menudo resulta necesario investigar los efectos de la ganancia o del período de
muestreo del sistema sobre la estabilidad absoluta y relativa del sistema en
lazo cerrado. Lo anterior se puede analizar aplicando el lugar geométrico de
las raíces (LGR) o el diagrama de Bode del sistema [22]. Los dos métodos mencionados
están disponibles en DIGITROLM. En la Fig. 8 se pueden observar los resultados
del análisis de estabilidad del sistema. Uno de ellos consiste en el diagrama
de Bode, el cual muestra la gráfica en el dominio de la frecuencia así como el margen
de ganancia y fase. El otro método muestra el trazo del LGR. En las dos
interfaces se habilita un mensaje indicando la estabilidad del sistema previamente
validada la información del análisis frecuencial para el diagrama de bode, o de
la ubicación de los polos sobre la circunferencia unitaria del plano Z para el
LGR.
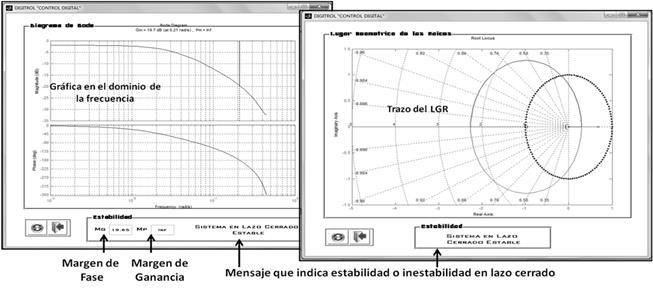
Fig.8. Interface con
los métodos para determinar estabilidad; aplicación DIGITROLM.
2.1.5 Controladores:
La etapa final en el proceso de diseño es el ajuste de los controladores. La aplicación
se diseñó de tal manera que para los sistemas POR permite ajustar controladores
convencionales proporcional (P), proporcional más integral (PI) y proporcional
más integral más derivativo (PID), mediante los métodos de ganancia limite,
curva de reacción y los criterios de error mínimo ISE (Integral Squared Error),
IAE (Integral Absolute Error), IAET (Integral Time Absolute Error).
Adicionalmente se pueden diseñar controladores digitales mediante los
algoritmos de Dalhin, Deadbeat de orden normal y Deadbeat de orden incrementado
para sistemas POR y SOR
En la Fig. 9 se muestra la interfaz para el ajuste y de
diseño de los controladores, en ella el usuario encontrará la respuesta de la
planta discretizada así como la opción para diseñar, ajustar y simular la respuesta
del proceso controlado. En la gráfica se puede visualizar la respuesta de la
planta controlada ante cambios en el set point que debe ser el mismo escalón
usado para la identificación del sistema, ya que es el punto de operación seleccionado
para el sistema, esto no implica que el controlador no haga su tarea en el
resto del rango de trabajo del sistema, pero si es de esperar que en este punto
se tenga un buen desempaño del controlador, y la respuesta del elemento final
de control, la gráfica es refrescada cada que se decida cambiar el ajuste del
controlador, los resultados numéricos del diseño o ajuste se muestran en cajas de
texto, marcadas con los nombres de los coeficientes a utilizar en la
implementación de la ley de control dada por (4), (5) y (6).
En un caso particular en el cual el diseño no sea el esperado,
el usuario dispondrá de todos los botones de opciones activos en la interfaz
principal. Esto permitirá cambiar si se requiere, la aproximación del modelo,
elegir un nuevo período de muestreo, cambiar el criterio de su elección, determinar
la estabilidad y realizar un nuevo ajuste que cumpla con el desempeño planteado
de acuerdo al proceso. Si la respuesta del diseño es la esperada, el usuario
podrá habilitar el módulo de implementación e ingresar los coeficientes del controlador
los cuales determinaran la señal de control aplicada al elemento final de
control.
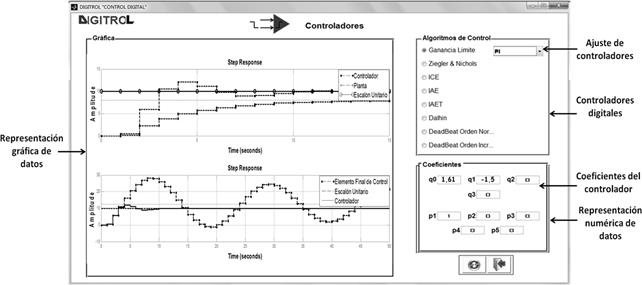
Fig.9. Interfaz con los
métodos de ajuste para los controladores; aplicación DIGITROLM.
2.3 Software para ajuste y simulación de controladores
PID
El segundo módulo de la aplicación fue denominado
DIGITROLL. Éste permite la implementación de los controladores diseñados en la
etapa de simulación o bien para otro diseño del cual se conozcan los coeficientes
de la ley de control dada por (5), (6) y (7). El módulo dispone de dos modos de
operación, uno para adquisición de datos y otro para implementación de
controladores (Fig. 10). En ambos modos de trabajo se debe configurar el
sistema de adquisición de datos, y la dirección donde el usuario desea
almacenar los valores de las variables que se miden y se controlan con el fin
de poder hacer análisis posteriores. Para cualquiera de los dos modos de trabajo
posibles, se cuenta con indicadores gráficos y numéricos que permiten seguir
visualmente el comportamiento de las variables, así como del error de control.
2.3.1 Modo adquisición de datos:
en éste el usuario puede adquirir los datos necesarios para la identificación
del sistema y con los parámetros obtenidos ajustar los controladores para el
proceso. Los datos son almacenados en un archivo de texto en formato .txt, el
cual puede ser interpretado en múltiples plataformas e.g. Matlab® y Excel. Los datos
se almacenan por columnas donde la primera corresponde al tiempo, la segunda a
la variable medida y la tercera corresponde a la salida hacia el elemento final
de control (EFC).
2.3.2 Modo control digital:
en éste el usuario puede controlar el proceso con los controladores obtenidos
para el sistema identificado y paramétrizado con los datos almacenados en el modo
de trabajo adquisición de datos. Para implementar el controlador solo basta
ingresar los coeficientes generados desde el módulo de diseño y simulación
DIGITROLM. Sin embargo, también se pueden ingresar los coeficientes calculados mediante
otros métodos siempre que estos puedan ser llevados a una ecuación en
diferencias como la mostrada en (7). Ésta última como resultado de la aplicación
de la trasformada (z) inversa a la función de trasferencia generalizada de un
controlador digital (4):
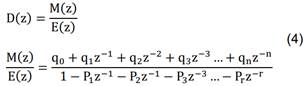
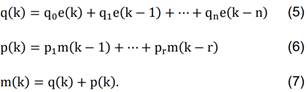
Donde:
m :
Corresponde a la ley de control.
e :
Corresponde al error de control.
La interfaz también permite adquirir datos del proceso
controlado. Los datos se almacenan por columnas donde la primera de ellas
corresponde al tiempo, la segunda al set point y la tercera corresponde a la
variable controlada. En la Fig. 10 se muestra la interfaz detallada del modo de
trabajo control digital.
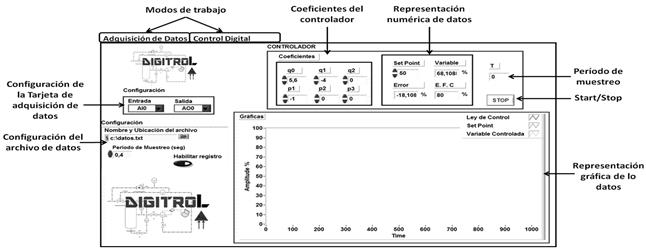
Fig.10. Interfaz
detallada para la implementación de controladores digitales, aplicación
DIGITROLL.
3. RESULTADOS
Para
observar los resultados de la aplicación se diseñaron controladores PID para
una planta de presión. La planta consiste en un módulo didáctico a escala que
emula un proceso industrial en el cual se almacena aire comprimido.
La
medición de la presión en el tanque de almacenamiento se mide mediante un
sensor de la serie MPX fabricado por freescaleTM. La variable manipulada se
refiere en este caso al voltaje aplicado al motor de corriente directa que
contiene la motobomba. El sistema cuenta con elementos que restringen el paso
del aire provocando a su vez retardos de transporte. En la Fig. 11 se muestra
el diagrama de proceso del sistema empleado. La planta de presión fue sometida
a estímulos de tipo escalón y en incrementos del 10% desde 0% al 100%, los
datos adquiridos fueron almacenados
desde
DIGITROLL y llevados a DIGITROLM para realizar el diseño y ajuste del
controlador, siguiendo el procedimiento ilustrado anteriormente.
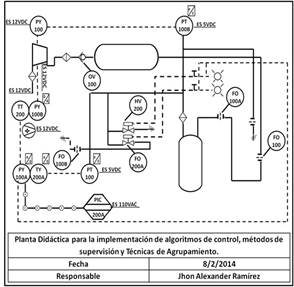
Figura 11. Diagrama de proceso e
instrumentación PI&D de la planta de presión, simplificado.
El
sistema se aproximó a un modelo POR cómo se muestra en (8), y se discretizó con
un período de muestreo T=12 s. Para el modelo obtenido se sintonizó un
controlador PI por el método de la ganancia última. Los coeficientes y
resultados de la simulación del controlador se muestran en la Fig. 12.
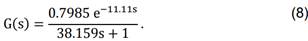
Los resultados deben ser presentados en una secuencia lógica en el
texto, tablas y figuras, se debe evitar la presentación repetida de los mismos
datos en diferentes formas (en el anexo 1 se explica como presentar ecuaciones,
figuras y tablas). Los resultados no deben contener material apropiado para
discusión. Al describir los resultados de los experimentos de los autores, esto
debe ser escrito en tiempo pasado. Los resultados deben ser explicados, pero en
gran parte sin hacer referencia a la literatura.
Los
coeficientes del controlador fueron ingresados en DIGITROLL. Para disminuir el
esfuerzo de control generado por el algoritmo de control en el sistema
controlado se ponderaron los coeficientes llevando la constante proporcional a
la mitad de su valor. La Fig. 13 muestra el comportamiento de la planta con el
controlador diseñado e implementado. Como se
puede
ver la respuesta de la planta presenta el comportamiento esperado desde la simulación
del controlador diseñado, es decir se esperan oscilaciones por encima del set
point, error de estado estacionario de cero y estabilidad en un tiempo finito
(aproximadamente 200 s.)
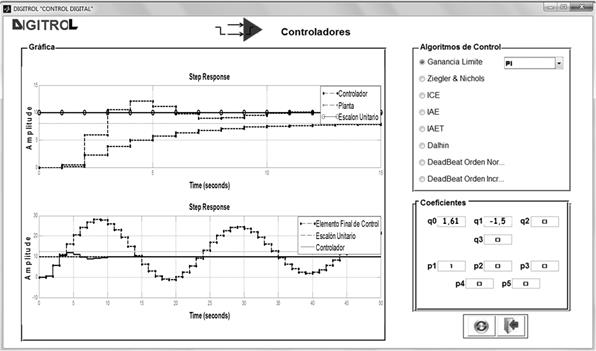
Fig.12. Resultados de la simulación del
controlador PI para la planta de presión
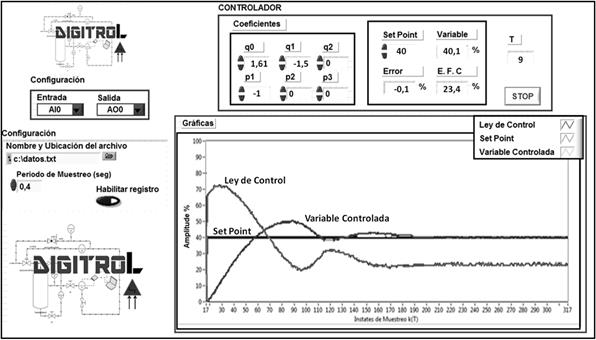
Fig.13. Resultados de la implementación del
controlador PI para la planta de presión
4. CONCLUSIONES
En
las herramientas de diseño, ajuste e implementación de controladores mostradas
se pueden trabajar de forma independiente, la teoría de control y la
implementación. Además, las herramientas presentan una alta flexibilidad con relación
al modelado de sistemas, ajuste, diseño y simulación de controladores debido a
que la base de datos, necesaria para el modelado, puede provenir de una planta
diferente a la mostrada en este documento.
El
diseño del software se hizo para que fuera amigable con el usuario, dotándolo
de elementos que lo llevan paso a paso por las diferentes etapas de la
identificación, simulación e implementación del controlador.
Se
evidenció la importancia de la simulación antes de la implementación de un
controlador en la planta real, ya que mediante está se pueden detectar aspectos
no deseados en el sistema de control e.g. un alto esfuerzo de control sobre el
EFC, sobre impulsos elevados en la variable controlada, y oscilaciones en la
ley de control entre otros que se pueden evitar en la implementación mediante
el rediseño del controlador o simplemente ponderando los valores de los
parámetros obtenidos para el controlador.
La
herramienta desarrollada para el ajuste, diseño y simulación ayuda a evaluar el
comportamiento del sistema ante varios controladores y permite de forma fácil
determinar cuál de todos es el adecuado de acuerdo a las condiciones deseadas
de diseño para implementar en la planta a controlar.
5. AGRADECIMIENTOS
Los
autores agradecen al Politécnico Colombiano Jaime Isaza Cadavid por permitir
los estudios previos para el desarrollo del este trabajo.
6. Referencias Bibliográficas
[1]
Alfaro V.M, Arrieta O., Vilanova R., Control de Dos-Grados-de-Libertad (2-GdL)
aplicados al “Benchmark” de Sistemas para Controladores PID. Revista
Iberoamericana de Automática e Informática Industrial. Vol. 6, Núm. 2, pp.
59-67, Abril 2009. Revista Politécnica ISSN 1900-2351 (Impreso), ISSN
2256-5353 (En línea), Año 12, Número 23, páginas 27-37, Julio – Diciembre 2016 37
[2]
O’Dwyer Aidan. Handbook of PI and PID Controller Tuning Rules (2.a ed.).
London: Imperial College Press, 2006.
[3]
Aliane N, Herramienta de Análisis y Diseño de Sistemas de Control Basada en
Hojas de Cálculo Excel. Revista Iberoamericana de Automática e Informática
Industrial, Vol. 6, Núm. 4, pp. 44-50 Octubre 2009.
[4]
Alfaro V.M, Identificación de Modelos de Orden Reducido a Partir de la Curva de
Reacción del Proceso. Ciencia y Tecnología, pp. 197-216, 2006.
[5]
Chivu C, Simulation of a Controller for a SDM System Using Matlab. Academic
Journal of Manufacturing Engineering, Vol 10, pp. 1-11, 2012.
[6]
Guo L, Han J, Otieno W, Design and Simulation of a Sun Tracking Solar Power
System. 120th ASEE Annual Conference & Exposition, Atlanta, June 23-26,
2013.
[7]
Yun C., Li X., Design of UAV Flight Simulation Software Based on Simulation.
WSEAS TRANSACTIONS on INFORMATION SCIENCE and APPLICATIONS, Vol 10, pp 37-46,
2013.
[8]
Ruano M.V., Ribes J., Seco A., Ferrer J., DSC: Software tool for
simulation-based design of control strategies applied to wastewater treatment
plants. Water Science & Technology, pp 796-803, 2011.
[9]
Cañas N., Hernández W., González G., Sergiyenko O, Controladores multivariables
para un vehículo autónomo terrestre: Comparación basada en la fiabilidad del
software, Revista Iberoamericana de Automática e Informática Industrial. Núm.
11, pp. 179-190, 2014.
[10]
Santana I., Ferre M., Hernández L., Aracil R., Rodríguez Y., Pinto E.,
Aplicación del Sistema de Laboratorios a Distancia en Asignaturas de Regulación
Automática, Revista Iberoamericana de Automática e Informática Industrial, Vol.
7, Núm. 1, pp. 179-190, Enero 2010.
[11]
De la Cruz F, Granados M, Zerpa S, Giménez D, Web-LABAI: Laboratorio Remoto de Automatización
Industrial, Revista Iberoamericana de Automática e Informática Industrial, Vol.
7, Núm. 1, pp. 101-106, Enero 2010.
[12]
Salcedo R., Corre R., SICOMPC: Simulador para Control Predictivo Basado en
Modelos, Dyna, Vol. 75, Núm. 156, pp. 89-98, Noviembre 2008.
[13]
Barrero L, Escobar A, Aspectos prácticos de implementación en compensadores PID
para control de posición de un automóvil, Ingenium, Vol.
15,
Núm. 29, pp. 148-162, mayo 2014. [14] Oravec J, Bakosová M, PIDDESIGN– Software
for System Identification and PID Controller Design, Selected Topics and
Control, Vol. 8, pp. 88-93, 2012.
[15]
Matlab. R2010a Documentation. Disponible en: http://www.mathworks.com/help/.
[Consultado en Junio de 2014].
[16]
Tan C., Teoh K., Jones L., A review of Matlab’s SISOTOOL; features and
contributions to Control education, Proceedings of the 17th World Congress The International
Federation of Automatic Control IFAC, Seoul, Korea, pp. 8473-8474, July 6-11,
2008
[17]
LabVIEW. NI Developer Zone. Disponible en: http://zone.ni.com/dzhp/app/main.
[Consultado en Octubre de 2014].
[18]
Aström J, Hägglund T, Revisiting the Ziegler– Nichols step response method for
PID control, Journal of Process Control, Vol. 14, pp. 635-650, 2004.
[19]
Johnson M., A. Moradi, PID Control New Identification and Design Methods,
Springer-Verlag London Limited, ISBN: 1852337028, pp. 70-80, London, 2005.
[20]
Alfaro V., Identificación de Procesos Sobreamortiguados Utilizando Técnicas de
Lazo Abierto, Ingeniería, Vol. 11, pp. 11-25, 2001.
[21]
García L., Sistemas de control digital, Teoría y práctica, Politécnico
Colombiano JIC, ISBN: 978-958-9090-25-1, pp 34-37. Medellín. Colombia. 2012
[22]
Ogata, K., Sistemas de control en tiempo discreto (4.a ed.). México: Prentice
Hall Hispanoamericana, S.A., 2002.



![]() ) y tiempo de retardo (Td),
como se muestra en la ecuación (1), este modelo es usado para sintonización de controladores
convencionales, por ejemplo las tablas de ajuste dadas por Ziegler-Nichols [2],
[18]. El modelo SOR es caracterizado por cuatro parámetros: ganancia (k),
frecuencia natural (ωn),
factor de amortiguamiento (ߞ
) y tiempo de retardo (Td),
como se muestra en la ecuación (2) [19].
) y tiempo de retardo (Td),
como se muestra en la ecuación (1), este modelo es usado para sintonización de controladores
convencionales, por ejemplo las tablas de ajuste dadas por Ziegler-Nichols [2],
[18]. El modelo SOR es caracterizado por cuatro parámetros: ganancia (k),
frecuencia natural (ωn),
factor de amortiguamiento (ߞ
) y tiempo de retardo (Td),
como se muestra en la ecuación (2) [19].