1. INTRODUCCIÓN
La célula eucariota como entidad dinámica está integrada por múltiples estructuras en su interior con funciones y morfologías particulares (como el núcleo, retículo endoplasmático, lisosomas, mitocondria, microsomas), que cumplen actividades vitales para su funcionamiento. Los procesos que tienen lugar en las células son complejos y la comprensión de la relación entre ese dinamismo a niveles intracelulares y su función biológica es una cuestión emergente en la biología celular y la biofísica [1]. La dinámica celular a escala nanométrica en moléculas biológicas (del orden entre y , comprende procesos de formación (y destrucción) de los complejos de replicación en el núcleo, de complejos de traducción en el citosol, y complejos de transición de permeabilidad en las mitocondrias [2]. Las mitocondrias, del griego mitos que significa hilo y khóndrion gránulo, fueron descubiertas hace más de un siglo por Richard Altman, quien las identificó como responsables de ciertas funciones vitales y presentes en prácticamente todas las células eucariotas [3,4]. En su organización interna las mitocondrias están conformadas por dos membranas, una externa y otra interna. La membrana externa, se encarga de realizar algunas funciones enzimáticas y de transporte. La membrana interna, carece de poros y realiza funciones más complejas relacionadas con la respiración celular y los fenómenos de transformación energética; su estructura presenta un patrón en forma de invaginaciones llamadas crestas. Algunas poseen diferentes tipos de forma en sus crestas: tubular, laminar, helicoidal y otras más complejas [5,6].
El desarrollo de la microscopía óptica ha permitido avanzar a la resolución nanométrica proporcionando la iniciativa hacia la microscopía electrónica y nuevas técnicas. Las primeras imágenes sobre la estructura mitocondrial aparecieron en los años cincuenta con el uso del microscopio electrónico el cual, a diferencia del microscopio convencional, utiliza electrones para formar imágenes. Es así como el biólogo rumano George Palade y el físico e histólogo sueco Fritiof Sjöstrand, observaron distintos elementos estructurales de estos orgánulos como la membrana externa, la membrana interna y las crestas mitocondriales, con un diámetro de alrededor [7]. Una característica general de la mayoría de las técnicas están basadas en
Microscopía de Localización Fotoactiva (PhotoActivated Localization Microscopy, PALM) o Microscopía de Reconstrucción Óptica Estocástica (Stochastic Optical Reconstruction Microscopy, STORM) [8], en ellas el uso de muestras biológicas finas, combinadas con la reflexión total interna, permite obtener imágenes de distribuciones de las proteínas en las células con una precisión de localización lateral de hasta en múltiples planos de imágenes de profundidad. Otra de las técnicas utilizadas es la nanoscopía fotoacústica, con ella se analizan imágenes a nivel celular o subcelular (como las mitocondrias en los fibroblastos y los melanosomas en las células del melanoma), esta técnica es sensible a la absorción óptica y posee una resolución de [9,10]. Existe además una herramienta producto de la combinación de dos técnicas experimentales: Espectroscopia de correlación de Imagen de Fourier (Fourier Imaging Correlation Spectroscopy, FICS) y Microscopía Fluorescencia Video Digital (Digital Video Fluorescence Microscopy, DVFM), usadas para estudiar la dinámica de un orgánulo intracelular tan complejo como la mitocondria [11].
Desde un punto de vista óptico, los tejidos biológicos se caracterizan por presentar un “alto” grado de inhomogeneidades, consecuencia de la estructura celular, pues ésta contiene organelos (mitocondria y núcleo) de diversos tamaños y composiciones. Por lo tanto, los constituyentes del tejido intracelular y extracelular tienen índices de refracción diferentes a los de los organelos [12]. Se ha demostrado que las mitocondrias son las principales responsables del gran ángulo de dispersión de la luz (isotrópica y anisotrópica). Aproximadamente el 90% de la luz dispersada se debe a las mitocondrias. Esto se debe en parte a la compleja estructura interna de las mitocondrias y sus numerosos cambios de índice de refracción. Se han analizado y simulado patrones de dispersión en células humanas así como determinado algunos aspectos de la estructura celular directamente a partir procedimientos experimentales y con una adaptación de la teoría clásica de difracción de rayos X [13].
Estudios de imágenes con fluorescencia, también han contribuido al trabajo previo de la microscopía electrónica mostrando que el conjunto mitocondrial de la célula puede organizarse como una red
tubular interconectada y extenderse en todo el interior de la célula, ocupando aproximadamente el 20% del volumen celular. Las pruebas de fluorescencia, muestran que las mitocondrias tienen filamentos, con un diámetro comprendido entre 100 y 500 nm, y una longitud de alrededor de 10 um. Los filamentos en forma de tubo se someten constantemente a cambios en la forma. Los filamentos de mitocondria que aparecen en imágenes de microscopia electrónica al realizar un corte transversal, muestran una serie de capas alternadas de matriz y espacio intermembrana, con una distancia d=10nm [14]. En el trabajo reportado por R. Thar and M. Kül [5], se representa un modelo simplificado de la mitocondria mediante el cual se estudia las propiedades ópticas de un sistema de multicapas.
Desde un punto de vista físico, una multicapa está hecha por dos o más medios materiales diferentes dispuestos alternadamente. Su uso va desde la fabricación de espejos con distribución tipo chirped [15, 16], el diseño de reflectores usando serie de Fibonacci [17], hasta algoritmos genéticos [18]. El estudio de la propagación de ondas en multicapas tiene sus inicios en los trabajos de Rayleigh [19], estableciendo las bases teóricas para el estudio de los cristales fotónicos [20, 21]. Los cristales fotónicos son semiconductores de luz, en ellos la luz siempre encuentra alguna dirección por la que pueden propagarse a través del cristal y se hace referencia al gap fotónico, como el rango de frecuencias prohibidas donde no existe propagación de la luz [22]. ]. Los cristales fotónicos son semiconductores de luz, en ellos la luz siempre encuentra alguna dirección por la que pueden propagarse a través del cristal y se hace referencia al gap fotónico, como el rango de frecuencias prohibidas donde no existe propagación de la luz [22].
Según la descripción realizada anteriormente, podemos hacer uso de un modelo físico matemático similar a los reportados en multicapas para estudiar el comportamiento de la luz en la mitocondria. A continuación se realiza el planteamiento del problema para luego presentar el método de la matriz de transferencia (MMT) con el cual se permite determinar los flujos de energía reflejada (reflectancia) y transmitida (transmitancia) en el sistema considerado. Por último, los resultados numéricos obtenidos.
2. MÉTODOS
El modelo óptico ideal que representa una mitocondria se describe a continuación:
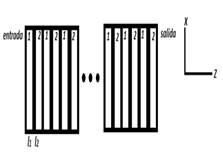
Fig. 1. Modelo simplificado de una mitocondria ideal. Se representa un sistema periódico de multicapas unidimensional formado por medios de índices de refracción diferentes n1 y n2 , y de espesores l1 y l2 , respectivamente.
Como se observa en la Fig. 1, la mitocondria se puede modelar como un medio periódico donde la luz puede propagarse. Para ello consideramos la incidencia de la onda electromagnética plana monocromática desde un medio caracterizado por un índice de refracción ni y con un ángulo de incidencia 0. El medio de salida de la onda electromagnética tiene un índice de refracción ns y el sistema está formado por N bicapas de medios alternados no dispersivos con índices de refracción n1 y n2 , cada uno de ellos de espesor l1 y l2. Para estudiar la propagación de la luz en la estructura mitocondrial simplificada, utilizamos el método de la matriz transferencia (MMT) con ella determinamos los espectros de la reflectancia R y transmitancia T en función de la longitud de onda de la luz incidente.
3 MÉTODO DE LA MATRIZ TRANSFERENCIA (MMT)
La teoría electromagnética viene condensada en las ecuaciones de Maxwell, que en forma diferencial se escriben [23]: explicados, pero en gran parte sin hacer referencia a la literatura.
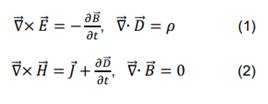
Donde
y 
son los vectores de campo eléctrico y de
desplazamiento eléctrico, respectivamente. De igual manera 
y 
representan los vectores de inducción y de
campo magnético. Las fuentes de los campos electromagnéticos son la densidad volumétrica
de carga eléctrica y la densidad de corriente eléctrica . Las leyes de Faraday
y de Gauss se representan por la ecuación (1). En la ecuación (2), tenemos la
ley de Ampere-Maxwell y la expresión que establece la ausencia de monopolos
magnéticos [24]. Las ecuaciones de Maxwell se complementan con las relaciones materiales,
que en medios lineales, homogéneos e isótropos vienen dadas por [25]:
En la ecuación (3),ꞓ y µ representan la permitividad dieléctrica y permeabilidad magnética, respectivamente.
En
lo que sigue, se estudia la propagación luz sin considerar las fuentes de los
campos electromagnéticos,P=0 y 
. La ecuación que rige la propagación de la luz
viene determinada por la ecuación diferencial [26]:
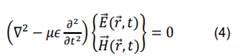
Las soluciones de interés de la ecuación (4) son las ondas planas monocromáticas,
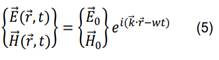
En
la ecuación (5),
representa el vector de onda, w es la
frecuencia angular y las amplitudes constantes complejas de los campos son 0 y 0 En la Fig. 1, la onda electromagnética
incide sobre la interface (plano XY) con un ángulo 
respecto a la normal al plano. La onda electromagnética,
con respecto al plano de incidencia XZ, tiene una componente perpendicular
(polarización s) y una componente paralela (polarización p).
El vector de onda incidente tiene componentes:
y
su módulo es ki
, siendo c la velocidad de la luz en el vacío.
Los medios que conforman el sistema periódico en la Fig. 1 son homogéneos en X,
por lo tanto los índices de refracción no varían en esa dirección. A medida que
la onda electromagnética se propaga, experimenta múltiples reflexiones en cada
una de las interfaces. Para la polarización s, el campo eléctrico está constituido
por la onda que viaja a la derecha (+Z) y otra a la izquierda (-Z), y se
escribe [27]:
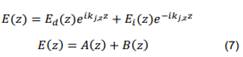
En la ecuación (7), el subíndice j representa el medio en el que la onda se propaga, para nuestro caso j=1, 2. Los dos tipos de ondas (izquierda y derecha) las representamos por A(Z) y B(Z). El módulo del campo eléctrico en cada uno de los medios se escribe [28]:
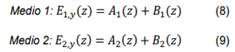
Reemplazando la ecuación (5) en la ley de Faraday y al tener en cuenta las componentes del vector de onda dado por la ecuación (6), se obtiene el vector de campo magnético en cada medio,
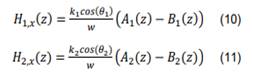
K1 (K2 y Ө1(Ө2 ) representan el módulo del vector de onda y el ángulo en el medio 1 (medio 2), respectivamente. Para determinar las funciones A(Z) y B(Z) que aparecen en la ecuación (10) y en la ecuación (11), se imponen las condiciones de continuidad en las fronteras para las componentes tangenciales de los campos [29]. En particular, el campo eléctrico es continuo en Y y el campo magnético es continuo en X, al efectuar los cálculos algebraicos se obtiene un sistema de ecuaciones que se condensan de la siguiente forma [30]:
En donde hemos definido [31],
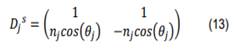
como la matriz dinámica para la polarización s
Para la polarización p, se sigue el mismo procedimiento anteriormente descrito y se obtiene:
La onda electromagnética se refracta en cada una de las fronteras de división, la matriz de transmisión entre los medios es:
El cambio de fase en la dirección Z, está dado por
En la ecuación (16), se toma el signo positivo para ondas que se propagan a la derecha y signo negativo para ondas que se propagan a la izquierda, Li representa el espesor de los medios que se está considerando. Se define la matriz de propagación como [32]:
A medida que la onda electromagnética se propaga en el sistema, experimenta múltiples reflexiones y refracciones. En general, la matriz característica del sistema representado por la Fig. 1, se escribe mediante
Los flujos de energía reflejada (reflectancia R) y transmitida (transmitancia T), se obtienen mediante las siguientes ecuaciones:
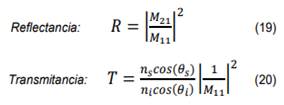
Donde M11 y M21 representan los elementos matriciales de la matriz característica dada por la ecuación (18). A continuación presentamos las simulaciones numéricas obtenidas para los cálculos de los flujos de energía reflejados, utilizaremos los parámetros de la mitocondria reportados en la referencia [5].
4 RESULTADOS
4
Con base al sistema descrito por la Fig. 1, consideramos que el medio de entrada y el de salida son iguales, para el caso de interés éste corresponde al citoplasma, con índice de refracción ni=ns=1,35 . Los índices de refracción para los medios que conforman la membrana son: medio 1 (matriz y membrana interna) n1= 1,5con espesor L1=50 nm , medio 2 (espacio intermembrana) n2=1,35 con espesor L2= 50 nm
Para la polarización s, los espectros de reflectancia y transmitancia en función de la longitud de onda del campo incidente normal sobre el sistema formado por N=20 bicapas, se muestra en la Fig. 2 y Fig. 3, respectivamente. Los resultados reportados en las Fig. 2 y Fig. 3 coinciden con los de la referencia [5], al tener en cuenta que el índice de refracción de la mitocondria es más alto que el índice de refracción del citoplasma que la rodea; el retículo mitocondrial puede actuar como una guía de onda óptica. Es decir, la luz en ciertos intervalos de longitud de onda puede propagarse a través de toda la estructura periódica.
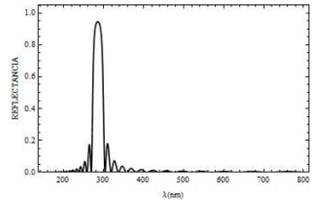
Fig. 2. Curva de reflectancia para un campo con polarización s, el cual incide sobre la mitocondria a
un ángulo Ө =0° y con N=20 bicapas.
Para longitudes de onda superiores a ,400 nm el campo electromagnético incidente logra atravesar el sistema ya que el flujo de energía dado por la transmitancia es máxima (T = 1 ). Para longitudes de onda de ,300 nm la reflectancia es máxima, el campo incidente es reflejado en un .95%
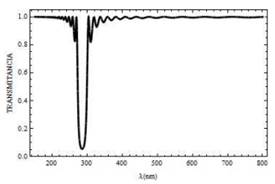
Fig. 3. Curva de transmitancia para un campo con polarización s, el cual incide sobre la mitocondria a un ángulo Ө= 0° y con N= 20 bicapas.
En la Fig. 3 se muestra que la existencia de un gap (o banda prohibida) de frecuencias, comprendido entre 260 y 300nm, aproximadamente. Dentro de ese rango, la luz no puede propagarse, R =1. A medida que el número de bicapas N aumenta, las oscilaciones que experimentan los espectros de reflectancia (Fig. 4) y transmitancia (Fig. 5), disminuyen. Favoreciendo así la canalización de la luz a través de la mitocondria con longitudes de onda por encima de 350 nm, a diferencia de los resultados reportados en la Fig. 3 donde la canalización ocurre para longitudes de onda superiores a 400 nm. Sumado a esto existe un corrimiento del gap entre 280 y 290 nm .
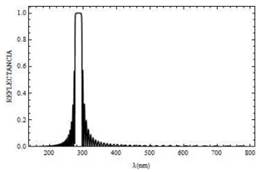
Fig. 4. Curva de reflectancia para un campo con polarización s, el cual incide sobre la mitocondria a un ángulo Ө=0° y con N=50 bicapas.
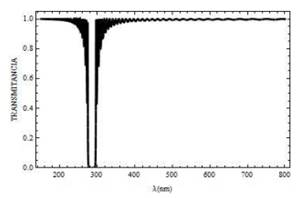
Fig. 5. Curva de transmitancia para un campo con polarización s, el cual incide sobre la mitocondria a un ángulo Ө=0° y N=50 con bicapas.
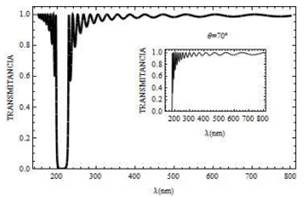
Fig. 6. Curva de transmitancia para un campo con polarización s, el cual incide sobre la mitocondria a un ángulo Ө = 45° (y Ө=70° curva en recuadro pequeño) N= 20 para bicapas.
Adicionalmente extendemos los resultados reportados en la referencia [5], al presentar en la Fig. 6 las curvas de transmitancia cuando el ángulo de incidencia de la luz aumenta. Para Ө=45° existe un corrimiento del gap para frecuencias grandes (longitudes de onda pequeñas) entre 200 y 230 nm , aproximadamente. En la curva de recuadro pequeño se considera que el ángulo de incidencia es ,Ө=70° se observa que la propagación de la luz solamente puedes ocurrir para longitudes de onda mayor a 200 nm, para valores menores, la luz es completamente reflejada R=1, como se muestra en la Fig. 7.
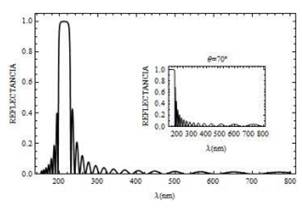
Fig. 7. Curva de reflectancia para un campo con polarización s, el cual incide sobre la mitocondria a un ángulo Ө = 45° (y Ө = 70° curva en recuadro pequeño) para ,N = 20 bicapas.
En las curvas de transmitancia Fig. 8 y reflectancia Fig. 9, consideramos la polarización p y el ángulo de incidencia de .Ө = 45° En ambos casos se presenta la variación de los espectros cuando aumentamos el número de bicapas N. Se observa para este tipo de polarización que la propagación de la luz es canalizada en la mitocondria cuando la longitud de onda se encuentra por encima de 210 nm. Sin embargo, cuando la longitud de onda es aproximadamente igual a 209.6 nm para N = 50, parcialmente cierta energía es reflejada y otra transmitida en el sistema.
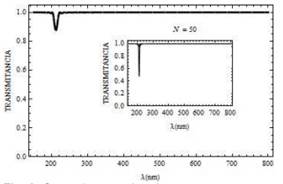
Fig. 8. Curva de transmitancia para un campo con polarización p, para Ө = 45° con N = 20 bicapas (y N= 50bicapas curva en recuadro pequeño).
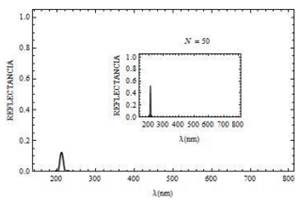
Fig. 9. Curva de reflectancia para un campo con polarización p, para Ө = 45° con N = 20 bicapas (y N = 50 curva en recuadro pequeño).
5 CONCLUSIONES
Presentamos un modelo simplificado de la mitocondria como un sistema periódico de multicapas. Haciendo uso del método de la matriz transferencia se observa que para ciertos valores de longitudes de onda la luz puede propagarse a través de la mitocondria como si fuese una guía de onda. Se muestra una dependencia con el número de bicapas que constituyen al sistema (mitocondria). El número de picos en las curvas de transmitancia y reflectancia para el sistema formado con un periodo de 50 bicapas es mayor que el número de picos de transmisión con un periodo de 20 bicapas. De igual manera existe una dependencia de las relaciones energéticas con el ángulo de incidencia Ө .Se presenta un corrimiento del gap para longitudes de onda menores (frecuencias altas) para obtener una reflectancia máxima, a medida que se aumenta el ángulo de incidencia.
6 AGRADECIMIENTOS
Los estudios preliminares presentados en el presente trabajo, fueron realizados gracias a la Universidad Surcolombiana por su apoyo en la financiación del proyecto semillero titulado: “Formulación física matemática de los problemas no lineales a escalas micro y macroscópica”, 2 de marzo del 2016.
7 Referencias Bibliográficas
[1] L.P. Gartner y J. L. Hiatt. Atlas color de histología. Médica Panamericana, Colombia, 2003.
[2] D. Margineantu, R. A. Capaldi, and A. H.Marcus.
Dynamics of the Mitochondrial Reticulum in LiveCells
using Fourier Imaging Correlation Spectroscopy and
Digital Video Microscopy. Biophysical Journal, 9,1833-1840, 2000.
[3] A. Martorell. Indagando el origen de las mitocondrias. Biol. On-line, 3, 1-18, 2014.
[4] G. Arboleda y R. M. Sánchez. Mitocondria y muerte celular. NOVA Publicación en Ciencias Biomédicas, 6, 190-200, 2008.
[5] R. Thar and M. Kül. Propagation of electromagnetic radiation in Mitochondria. Journal of theoretical biology, 230, 261-270, 2004.
[6] J. Guevara, D. Matuz y H. Vázquez. La mitocondria en el centro del universo celular. Mensaje bioquímico, 36, 65-81, 2012.
[7] Martorell R. Regulación de la dinámica mitocondrial en neuronas sometidas a excitotoxicidad [PhD Tesis]. Barcelona: Universitat de Barcelona, 2014.
[8] A. Vaziri, J. Tang, H. Shroff, and C.V. Shank. Multilayer three-dimensional super resolution imaging of thick biological samples, Proceedings of the National Academy of Sciences, 105, 20221-20226, 2008.
[9] A. Danielli, K, Maslov, A. Garcia Uribe, A. M. Winkler, C. Li, L. Wang, Y. Chen, G.W. Dorn II, and L. V. Wanga. Label-free photoacoustic nanoscopy. Journal of Biomedical Optics, 19, 086006-086006,2014.
[10] S.L. Chen, L. Guo and X. WANG. All-optical photoacoustic microscopy. Photoacoustics, 3, 143-150, 2015.
[11] K. Kladko, I. Mitkov and A. R. Bishop. Universal scaling of wave propagation failure in arrays of coupled nonlinear cells. Physical review letters, 84, 4505, 2000.
[12] V. Tuchin. Tissue optics: light scattering methods and instruments for medical diagnosis. Bellingham, SPIE, 2007.
[13] P. Pilarski. Rapid simulation of wide-angle scattering from mitochondria in single cells. Optics express, 16, 12819-12834, 2008.
[14] M. Cifra. Electric field generated by axial longitudinal vibration modes of microtubule. BioSystems, 100, 122-131, 2010.
[15] B. Agarwal, J. Broutman and K. Chandrashekhara. Analysis and performance of fiber composites. John Wiley & Sons, 2006.
[16] J. Estevez. Enlargement of omnidirectional photonic bandgap in porous silicon dielectric mirrors with a Gaussian profile refractive index. Applied physics letters, 94, 061914, 2009.
[17] N. Grushina. Broad omnidirectional band of reflection from Fibonacci one-dimensional photonic crystals. PIERS, 5, 511-515, 2009.
[18] W. Jiang. Nanoparticle-mediated celular response is size-dependent. Nature nanotechnology, 3, 145-150, 2008.
[19] L. Rayleigh. On the influence of obstacles arranged in rectangular order upon the properties of a medium. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 211, 481-502, 1892.
[20] E.Yablonovitch. Inhibited spontaneous emission in solid-state physics and electronics. Physical review letters, 58, 2059, 1987.
[21] J. Sajeev. Localization of light. Phys. Today, 44, 32-40, 1991.[22] J. Joannopoulos. Photonic crystals: molding the flow of light. Princeton university press, 2011.
[23] E. Hecht. Optics. 4th Edition, Addison Wesley Longman, USA, 1998.
[24] W. Greiner. Classical Electrodynamics. Springer science, USA, 2012.[25] W. Callister and D. Rethwisch. Materials science and engineering: an introduction. Wiley,New York, 2007.
[26] A. Sepulveda. Electromagnetismo. Universidad de Antioquía, Medellin, 2009.
[27] A. Kavokin, J. Baumberg, G. Malpuech and F. Laussy. Microcavities. Oxford University Press, New York, 2007.
[28] S. Chuang. Physics of optoelectronic devices. Wiley Interscience, New York, 1995.[29] I. Grant and W. Phillips. Electromagnetism.Jhon Wiley and Sons, USA, 2013.
[30] M. Cottam and D. Tilley. Introduction to Surface and superlattice excitations. CRC Press, 2004.
[31] A. Lipson, S. Lipson and H. Lipson. Optical physics. Cambridge University Press, 2010.
[32] T. Zhang. Transfer matrix method for optics in graphene layers. Journal of Physics: Condensed Matter, 25, 215301, 2013.