ARTÍCULOS

EFECTO DE LA CONFIGURACIÓN AFFINE EN EL ALGORITMO ACELERADOR REGRESIVO: VERSIÓN γ (ARγ)

THE EFFECT OF THE AFFINE CONFIGURATION IN THE ALGORITHM ACCELERATOR REGRESSIVE VERSION γ (ARγ)

María Fernanda Rivera Sanclemente¹ y Pablo Emilio Jojoa Gomez²

1 Ph.D. (c) en Ingeniera Electrónica, Universidad del Cauca. E-mail: mfrivera@unicauca.edu.co.

2 Ph.D Ingeniero Electrónico, Docente, Universidad del Cauca. E-mail: pjojoa@unicauca.edu.co. Universidad del Cauca, calle 5 No. 4 – 70, Popayán, Colombia.

Recibido: 27 de febrero de 2014. Aceptado: 28 de octubre de 2014.
Received: February 27^th, 2014. Accepted: October 28^th, 2014.

RESUMEN

Una combinación affine realiza una suma ponderada de las salidas de dos filtros adaptativos sometidos a una misma entrada cuyo factor de ponderación es un parámetro calculado mediante un mecanismo adaptativo (filtros adaptativos) con el propósito de lograr un mejor rendimiento. En este trabajo ''Efecto de la configuración Affine en el Algoritmo Acelerador versión γ (ARγ)'', se operacionaliza el comportamiento de éste algoritmo en combinación Affine con el propósito de alcanzar una mayor eficiencia y un mejor rendimiento del algoritmo en su configuración básica; Así mismo, identificar sus efectos. Corresponde a un estudio descriptivo, explicativo y experimental dirigido a responder por qué ocurre un fenómeno (aplicación de la Combinación Affine en filtros adaptativos) y en qué condiciones se da éste; concluyendo que el efecto logrado al hacer aplicación de la configuración affine es un algoritmo adaptativo en el que no hay limitación en el parámetro de mezcla, ofrece buena velocidad de convergencia y gran capacidad de seguimiento (tracking); comportándose como el mejor de los filtros aliviando el compromiso entre la velocidad de convergencia y el error residual inherente al filtro.

Palabras clave: Filtros adaptativos, Algoritmo Acelerador versión γ (ARγ), Combinación Affine.

ABSTRACT

Affine combination takes a weighted sum of the outputs of two adaptive filters subjected to the same input whose weighting factor is a parameter calculated using an adaptive mechanism (adaptive filters) in order to achieve a better performance. This study operationalized the behavior of Algorithm Accelerator Version γ (ARγ) in Affine combination in order to achieve greater efficiency and better performance than the algorithm presented in its basic configuration; likewise identify the effects of the Affine Combination Algorithm Accelerator Version γ (ARγ) adaptive algorithm. The methodological design and operational plan are part of a research process with a descriptive, explanatory and directed experimental answer why the phenomenon occurs (application of adaptive filters in Affine Combination) and under what conditions it occurs.

Key words: Adaptive filters, Algorithm Accelerator Regressive Version γ (ARγ), Affine combination.

1. INTRODUCCIÓN

Existen distintas aplicaciones de los filtros adaptativos como por ejemplo: Sistemas de antena adaptativa, en los que dichos filtros son utilizados para dirigir el haz y proporcionar nulos en el patrón de haz eliminando las interferencias indeseadas [1]; Receptores digitales de comunicaciones, en éstos su utilización tiene como propósito ecualizar la interferencia intersímbolos y para identificar el canal [2][3]; Técnicas de cancelación de ruido adaptativas en las que se emplean para estimar y eliminar un componente de ruido de la señal deseada [4]; y el Modelado de sistemas en donde los filtros adaptativos son utilizados como modelos para estimar las características de un sistema desconocido [5]. Todas estas aplicaciones están referidas a sistemas que son variantes en el tiempo, razón por la que la aplicación de los filtros convencionales con parámetros fijos resultan inaplicables generando la necesidad de utilizar filtros cuyos coeficientes se ajustan en el tiempo. El ajuste de estos coeficientes se obtiene mediante un algoritmo matemático (algoritmo adaptativo o de adaptación) que minimiza una función de costo, función que puede corresponder a una medida de error existente entre lo que se espera como respuesta y lo que se obtiene del filtro cuyos parámetros se están ajustando a medida que pasa el tiempo. El algoritmo adaptativo entonces, ajustará los coeficientes del filtro teniendo en cuenta la señal de entrada, como también, una señal de referencia o señal deseada y una medida del error.

Esta medida de error puede ser manipulada utilizando diferentes criterios como el valor absoluto, el cuadrado mínimo o media cuadrática, siendo éstos últimos los más utilizados, conocidos en la literatura como los métodos de mínimos cuadrados (LS. Least Square) y error cuadrático medio (MSE. Mean Square Error); se reitera que la esencia de los filtros adaptativos es el algoritmo que ajusta los coeficientes. Se han diseñado varios algoritmos con coeficientes ajustables como por ejemplo el Least Mean Square (LMS) y sus derivados (NLMS, Leaky, etc.) o el Recursive Least Square (RLS) y sus derivados (FRLS, Kalman, etc.) algoritmos con los que se busca alcanzar un ajuste de sus coeficientes de forma rápida (rapidez de convergencia, lo que significa qué tan rápido el algoritmo llega al MSE – Means Square Error) buscando que la variación al rededor del mínimo (desajuste) sea pequeña y además capaz de seguir los cambios del ambiente de forma rápida (seguimiento o tracking)[6] siguiendo un procedimiento que implementa un modelo variante en el tiempo para un sistema de identificación o, un sistema modelado por un filtro transversal que sigue el proceso de Markov[6] de primer orden; características de los filtros adaptivos que se ilustrarán en el desarrollo del presente artículo.

Jojoa [7], diseña el algoritmo conocido como Acelerador Regresivo versión γ (ARγ) con características tales como buena velocidad de convergencia y paralelamente una considerable reducción del error de medida final. Como antecedente al algoritmo de Jojoa se disponía del Algoritmo Acelerador de Tiempo Continuo propuesto por F. Pait [8], caracterizado por permitir ajustar la segunda derivada (aceleración) del error con respecto a los coeficientes del algoritmo; su particularidad es la adquisición de un mayor compromiso entre la velocidad de convergencia y la variación del error de estimación en relación a los algoritmos de gradiente estocástico. Con base en las propiedades presentadas por el Algoritmo Acelerador de Tiempo Continuo se desarrolla un Algoritmo de Tiempo Discreto, del cual se obtienen tres versiones: el Algoritmo Acelerador Progresivo Convencional Matricial (APCM), el Algoritmo Acelerador Regresivo Convencional Matricial (ARCM) y el Algoritmo Acelerador Regresivo versión γ (ARγ)[7]. Versiones obtenidas utilizando los métodos de discretización de Euler y la transformación bilineal con resultados favorables respecto al desempeño y complejidad computacional.

El Algoritmo Acelerador Regresivo Versiónγ (ARγ) propuesto por Jojoa [6] corresponde a una versión simplificada del algoritmo ARCM, que tiene como principal característica la disminución del número de parámetros de ajuste de cuatro a tres (α, m₁ = m₁I_M, m₂ = m₂I_M y m₃ = m₃I_M) denominados α, γ y m₁, por medio de los cuales se logra una buena velocidad de convergencia y una considerable reducción del error de medida final [9]. La ventaja de este algoritmo es que los parámetros de ajuste se reducen a cantidades escalares (α, γ y m₁) .El análisis de convergencia con respecto a la media realizado por Jojoa establece que el algoritmo converge para valores de α , γ y m₁ positivos. Así mismo, el análisis de tracking del algoritmo ARγ en ambientes no estacionarios presenta un mínimo error de desajuste.

Posteriormente, Bershad, Bermúdez y Toumeret [10] utilizaron una nueva configuración para la implementación de filtros adaptativos con base en el algoritmo LMS, esta configuración es conocida como configuración Affine, novedoso esquema que consiste en la mezcla de dos filtros adaptativos W₁(n) y W₂(n) , cuyo fundamento es la selección escalar de un parámetro de mezcla λ(n) [11] para combinar las salidas de los dos filtros buscando obtener finalmente una tasa de convergencia más eficiente y un mejor estado de equilibrio por medio de un parámetro de adaptación µ_λ[12].

2. METODOLOGIA

ALGORITMO ACELERADOR REGRESIVO VERSIÓN γ (ARγ)

Buscando disminuir la complejidad computacional del algoritmo ARCM, Jojoa. [6] obtuvo el algoritmo (ARγ) como versión simplificada del algoritmo ARCM, cuya principal característica es la disminución del número de parámetros de ajuste de cuatro a tres (α, m₁ = m₁I_M, m₂ = m₂I_M y m₃ = m₃I_M) denominados (α, γ y m₁) , por medio de los cuales se logra una buena velocidad de convergencia como también una considerable reducción del error de medida final[13]. Las ecuaciones que describen el algoritmo ARγ son:

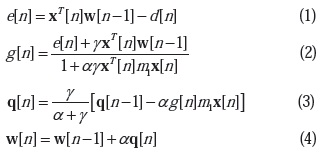
Propiedades del Algoritmo Acelerador Regresivo Versión γ (ARγ)

En este algoritmo los parámetros de ajuste se reducen a cantidades escalares (α, γ y m₁) .

El análisis de convergencia con respecto a la media establece que el algoritmo converge para valores positivos de α, γ y m₁. El análisis de Tracking del algoritmo ARγ , en ambientes no estacionarios presenta un mínimo de error de desajuste cuando α, γ y m₁ tienden a H (Criterio de Mínimo Error) en el cual H es una constante real positiva con un valor aproximado 2., como lo establecen algunos valores de H obtenidos por Jojoa [6] teórica y prácticamente para distintos valores de α , γ y m₁ con los que se obtiene un mínimo de desajuste.

COMBINACIÓN AFFINE

El esquema de la combinación Affine[14] consiste en la mezcla de dos filtros adaptativos que se ilustran como W₁(n) y W₂(n) en la Figura 1.

El fundamento de este método o Combinación Affine es la selección escalar de un parámetro de mezcla λ (n) para combinar la salida de los dos filtros buscando obtener finalmente una tasa de convergencia más eficiente y un mejor estado de equilibrio. En una combinación Affine como se dijo anteriormente se realiza una suma ponderada de las salidas de dos filtros adaptativos sometidos a una misma entrada cuyo factor de ponderación es un parámetro calculado mediante un mecanismo adaptativo (Filtros adaptativos) con la finalidad de obtener un mejor rendimiento [10].

3. RESULTADOS Y DISCUSIÓN: COMPORTAMIENTO DEL ALGORITMO ACELERADOR REGRESIVO VERSIÓN γ (ARγ) EN COMBINACIÓN AFFINE.

Para analizar el efecto de la Combinación Affine en el Algoritmo Acelerador Regresivo versiónγ (ARγ), se realizaron 5 experiencias donde se trabaja con base en la configuración de identificación de sistema, constituido por un filtro FIR de respuesta impulsiva h señal de entrada x(n) con ruido blanco gaussiano con media cero y σ² = 0.04 , señal deseada d. Los parámetros del sistema a identificar se suponen invariantes en el tiempo con valores entre -1 y 1 dado por

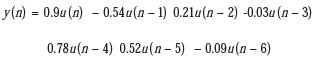
y para su observación durante las experiencias se usa un vector llamado B, orden del filtro M = 7, número de muestras N = 5000 y número de experiencias K =10.

Experiencia 1. Comportamiento del Algoritmo Acelerador Regresivo versión γ (ARγ) por parámetro μ_λ.

En esta experiencia se observa cómo se comporta el algoritmo acelerador en configuración affine al modificar el parámetro μ_λ (paso de adaptación del filtro en combinación Affine) teniendo fijos los parámetros de ajuste de los algoritmos aceleradores. Para observar su comportamiento se obtuvieron las Figuras 2 y 3 con valores iniciales.

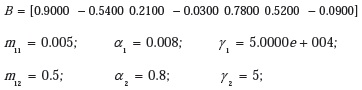
La Tabla 1 detalla la variación de μ_λ (paso de adaptación configuración Affine), el valor del error cuadrático medio para los algoritmos Acelerador ARγ en configuración Affine (ARγ Aff), Acelerador ARγ más lento (AR 1) y más rápido (AR 2), donde se observa que no hay un comportamiento lineal, pero a medida que se aumenta del valor de μ_λ = 0.5, el incremento de μ_λ hace que el error aumente, así mismo, a medida que μ_λ se acerca a cero el error aumenta.

Experiencia 2. Comportamiento Del Algoritmo Acelerador Regresivo Versión γ(Arγ) Por Parámetro m₁.

A continuación se ilustra el comportamiento del algoritmo acelerador en configuración Affine al tomar diferentes valores del parámetro m₁. Las Figuras 4 y 5 muestran este comportamiento, con valores iniciales:

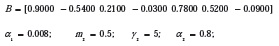
La Tabla 2 muestra la variación de μ_λ y m₁, el valor del error cuadrático medio para los algoritmos Aceleradores ARγ en configuración Affine. El Algoritmo Acelerador ARγ más lento (color rojo) y más rápido (color azul), se observa que μ_λ y γ₁ son inversamente proporcionales: a medida que aumenta μ_λ, disminuye γ₁. El mínimo error cuadrático medio se alcanza cuando μ_λ = 50 tanto para el algoritmo acelerador en configuración Affine y para el algoritmo AR_γ2 más rápido, siguen sin ser lineales a diferencia del algoritmo AR_γ1.

En las Figuras 4 y 5 se observa el comportamiento del algoritmo acelerador en configuración affine. En la Figura 4 donde μ_λ = 50 el algoritmo acelerador en configuración affine alcanza el mínimo error cuadrático medio pero cuando μ_λ = 127 del algoritmo en configuración Affine su comportamiento parece ser el más rápido.

Experiencia 3. Comportamiento del Algoritmo Acelerador Regresivo versión γ (ARγ) por parámetro m₂.

Se ilustra el comportamiento del algoritmo acelerador en configuración Affine al variar los valores del parámetro m₂. Las Figuras 6 y 7 muestran el comportamiento al tomar valores iniciales como:

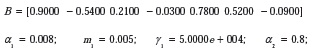
En la tabla 3 se especifica la variación de µ_λ y m₂; el valor del error cuadrático medio para los algoritmos Acelerador ARγ en configuración Affine, Acelerador ARγ más lento y más rápido.

Cuando m₂ = 50 y μ_λ = 2 el algoritmo en configuración affine alcanza el mínimo error cuadrático medio con un valor muy aproximado para el filtro ARγ2 Para μ_λ = 5 el algoritmo en configuración affine se comporta como el filtro más rápido hasta μ_λ = 50 donde se empieza a desajustar. El comportamiento con respecto al error sigue siendo no lineal con excepción del algoritmo ARγ1; los parámetros μ_λ y γ₂ siguen siendo inversamente proporcionales. A partir de μ_λ = 30 el algoritmo en configuración affine empieza a desajustarse como se ve en las figuras 6 y 7 Desde la experiencia 1 hasta la experiencia 3 el parámetro λ(n) ha tomado valores menores a 0.

Experiencia 4. Comportamiento del Algoritmo Acelerador Regresivo versión γ (ARγ) por parámetro α₁.

Se registra el comportamiento del algoritmo acelerador en configuración Affine al variar los valores del parámetro y con las Figuras 8 y 9 se puede observar el modo de comportarse al tomar valores iniciales así:

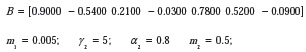
En la Tabla 4 se especifica la variación de α₁ observando los valores del error cuadrático medio para los algoritmos Acelerador ARγ en configuración Affine; Algoritmo Acelerador ARγ1 más lento y Algoritmo Acelerador ARγ2 más rápido.

En las Figuras 8 y 9 se plasma el comportamiento de los algoritmos observando que para μ_λ = 5 se obtiene el mínimo error cuadrático medio para el algoritmo en configuración affine, además se observa que en las Figuras 8 y 9 el comportamiento del algoritmo en configuración Affine es más rápido que los algoritmos ARγ en su configuración convencional.

Respecto al parámetro λ(n) en las Figuras 8 y 9 se observa que puede tomar valores tanto negativos como positivos.

Experiencia 5. Comportamiento del Algoritmo Acelerador Regresivo versión γ (ARγ) por parámetro α₂.

Registra el comportamiento del algoritmo acelerador en configuración Affine al variar los valores del parámetro α₂ y con las Figuras 10 y 11 se puede observar el modo de comportarse al tomar valores iniciales así:

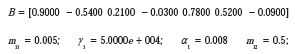
En la Tabla 5 se especifica la variación de μ_λ y α₂ observando los valores del error cuadrático medio para los algoritmos Acelerador ARγ en configuración Affine, Algoritmo Acelerador ARγ1 y ARγ2 más lento y más rápido respectivamente. Con las Figuras 10 y 11 se observa el comportamiento de los algoritmos con μ_λ = 10 y que corresponde al momento en que se obtiene el mínimo error cuadrático medio para el algoritmo en configuración affine como se ve en la Figura 11. El comportamiento del algoritmo en configuración Affine es más rápido que los algoritmos ARγ en su configuración convencional. Para valores de α₂ entre [10, 50] y μ_λ entre [0.5, 10] el error cuadrático medio no tiene un comportamiento lineal.

COMPORTAMIENTO DEL ALGORITMO ACELERADOR REGRESIVO VERSIÓN γ (ARγ) Y PROCESO DE MARKOV.

A continuación se examinará el comportamiento del algoritmo en un ambiente no estacionario siguiendo el procedimiento descrito en Hayking [6] el cual implementa un modelo variante en el tiempo para un sistema de identificación, o un sistema modelado por un filtro transversal que sigue un proceso de Markov de primer orden como se describe en la Figura 12.

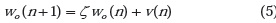
ζ = parametro fijo (aproximado a 1)

v(n) = vector de ruido con media cero

w_o(n) = coeficientes del sistema a ser identificado

η(n) = ruido blanco gaussiano con media cero y varianza

x(n), v(n) y η(n) = estadisticamente independientes

Para verificar el análisis se efectúan diferentes experiencias con las siguientes condiciones:

L = longitud de la señal L = 8000

σ²_v = varianza del Proceso de Markov = 0.01

σ²_x = varianza de la señal de entrada = 0.1

σ²_η = varianza del ruido de medida = 0.05

En la Figura 13. Se observa el mejor comportamiento con ς = 0.99

4. CONCLUSIONES

Para el efecto de la combinación de dos algoritmos, con el propósito de obtener un mejor rendimiento se lleva a cabo la utilización del Algoritmo Acelerador Regresivo versión γ (ARγ). Algoritmo descrito por Pablo Emilio Jojoa Gómez en 2003, que presenta como principal característica la disminución del número de parámetros de ajuste denominados: α, γ y m₁, con una buena velocidad de convergencia y una considerable reducción del error de medida final. Al algoritmo anterior se le aplica la configuración Affine registrando el comportamiento que presenta por medio de parámetros como λ que es el parámetro que permite la combinación y se observa que al hacer uso del Algoritmo Acelerador versión γ(ARγ) en combinación Affine se logra una buena adaptabilidad mejorando características como velocidad, reducción del error de medida final; buena capacidad de seguimiento (tracking) como se observa en la Figura 13 (ς = 0.99) y óptimos resultados en desajuste. El filtro combinado resultante tiende a comportarse como el mejor de los filtros, aliviando el compromiso entre la velocidad de convergencia y el error residual inherente al filtro.

Las características anteriormente descritas se evidencian en los registros obtenidos para las diferentes experiencias llevadas a cabo en el desarrollo del estudio. Algoritmo Acelerador Versión γ(ARγ) en configuración Affine, respecto a valores de µ_λ cercanos a cero el error cuadrático medio se incrementa sin presentar un comportamiento lineal que sí se observa en todas las experiencias llevadas a cabo. Así mismo su comportamiento resulta más lento con valores altos de µ como se ilustra en la Fig. 2. ofreciendo un comportamiento que puede ser calificado como el más rápido frente a valores µ_λ = 1, 5, 127 Igualmente se observa que en las experiencias llevadas a cabo el comportamiento del parámetro λ adquiere valores tanto positivos como negativos.

5. AGRADECIMIENTOS

Al Ing. PhD. Pablo Emilio Jojoa Gómez. Director del trabajo de tesis, y del grupo I+D en Nuevas Tecnologías en Telecomunicaciones-GNTT. A los ingenieros: Ph.D. Carlos Felipe Rengifo Rodas, MSc. Yudy Cristina Realpe Docentes Facultad Ingeniería Electrónica y MSc. Alexander Parrado de la Universidad del Quindio, que con sus aportes permitieron culminar con éxito este trabajo.

6. REFERENCIAS BIBLIOGRÁFICAS

[1] Windrow, B. Mantey, P y Griffiths, L. J. Adaptative Antenna Systems. IEEE, vol. 55, Pag. 2143-2159, Diciembre. 1967.

[2] Picinbono, B. Adaptive Signal Processing for Detection and Communication, en Communicatio Systems and Random Process Theory, J. K. Skwirzynski, ed., Sijthoff en Noordhoff, Alphen aan den Rijin, Paises Bajos. 1978.

[3] Nichols, H. E y Proakis, J. G. MLD and MSE Algorithms for Adaptive Detection of Digital Signals in the Precense of Interchannel Interference. IEEE Trans. Informations Theory, Vol. IT-23, págs. 1.7.1- 1.7.6, Hamilton, ON, Agosto. 1977.

[4] Ketchum, J. W. y Proakis, J. G. Adaptive Algorithms for Estimating and Suppressing Narrow- Band Interference in PN Spread-Spectrum Systems, IEEE Trans. Communications, Vol. COM- 30, págs.913-923, mayo. 1982.

[5] Proakis, J. G. y Manolakis, D. G. Tratamiento Digital de Señales, 4ed, Pearson Education S.A. Madrid. 2007.

[6] Haykin, S.) Adaptative Filter Theory, 3ra. Ed. Upper Saddle River, Prentice Hall, NJ, 4th edition. 2002.

[7]Jojoa, P.E. Um Algoritmo Acelerador de Parâmetros, Tesis de Doctorado. Escola Politécnica da Universidade de Sao Paulo, Brasil. 2003.

[8] Pait, F. A Tuner that Accelerates Parameters, Systems and Control Letters, vol. 35, n.1, pp. 65- 68. 1998.

[9] Choi, H. J.; Cho, H.; Jeong, J. J. y Kim, S. W. Combination of step sizes for affine projection algorithm with variable mixing parameter. Electronics Letters. Vol. 29, no. 18, Agosto. 2013.

[10] Bershad, N. Bermudez, J. y Tourneret, J. An Affine Combination of Two LMS Adaptive Filters– Transient Mean-Square Analysis IEEE Transactions on Signal Processing, vol. 56, no. 5, Mayo. 2008.

[11]Chun, S. H.; Kim, Y. H.; Choi, K. J.; Kim, J. Y.; Kim, J. H.; Kim, D. y H, C. K. Adaptive digital predistortions based on affine projection algorithm for WCDMA power amplifier applications. IEEE. 2010.

[12] Candido, R.; Silva, M. y Nascimento, V. Transient and Steady-State Analysis of the Affine Combination of Two Adaptive Filters. EEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, NO. 8, Agosto. 2010.

[13]Gerken, M.; Pait, F.; Jojoa P.E. An Adaptive Algorithm with Parameter Aceleration, IEEE International Conference on Acoustics, Speech and Signal Processings 2000. Istambul, 2000. CASSP'2000, CD-ROM. 2000.

[14] Kaleem, A. M y Tamboli, A. I. An Affine Combination of two time Varying LMS Adaptive Filters. International Conference on Communication, Information & Computing Technology (ICCICT), Oct. 19-20, Mumbai, India. 2012.