ARTÍCULOS

DISEÑO DE CONTROLADORES PI Y PID FRACCIONARIOS PARA REGULAR LA VELOCIDAD DE UN MOTOR DC UTILIZADO PARA MANEJAR UN GENERADOR DE ENERGÍA

DESIGN OF A FRACTIONAL PID CONTROLLER FOR A DC MOTOR USED FOR DRIVING A POWER GENERATOR

Luis Eduardo García Jaimes¹, Carlos Andrés Velásquez Ospina², Héctor Wilson López Espinosa³

1 Magister en Educación Universidad de Antioquia, Especialista en Automatización Industrial Universidad del Valle. E-mail: legarcia47@gmail.com.

2Ing. en Instrumentación y Control. Estudiante de maestría en informática énfasis en automatización y robótica de la universidad católica del norte, Antofagasta – Chile. E-mail: canveo@hotmail.com.

3 Ing. en Instrumentación y Control. Medellín - Colombia. E-mail: hwloes@hotmail.com.

Recibido: 25 de octubre de 2014. Aceptado: 16 de diciembre de 2014.
Received: October 25^th, 2014. Accepted: December 16^th, 2014.

RESUMEN

Se presenta el diseño de un controlador PID fraccionario para regular la velocidad de un motor de DC que mueve un generador de energía eléctrica y su desempeño es comparado con el de un controlador PID convencional sintonizado utilizando el método del lugar geométrico de las raíces. El trabajo se divide en tres partes así: en la primera parte se establece el comportamiento dinámico del sistema de generación de energía formado por dos motores de DC, uno funcionando como motor propiamente dicho y otro como generador, en la segunda parte, se plantean las bases teóricas del cálculo fraccionario y del diseño de controladores PID fraccionarios y, en la tercera parte, se diseñan e implementan los algoritmos de control PID fraccionario y PID convencionales para el sistema motor-generador y se compara el desempeño de los algoritmos diseñados. Los resultados obtenidos indican que el controlador PID fraccionario puede ser una buena opción para realizar el control de procesos industriales.

Palabras clave: sistema de control, PID fraccionario, NINTEGER, identificación, motor-generador.

ABSTRACT

The design of a fractional PID controller to regulate the speed of a DC motor driving an electric generator is presented and its performance compared with that of a conventional PID controller tuned using the root locus method. The work is divided into three parts as follows: in the first part the dynamic behavior of the system power generation consists of two DC motors, one running as the engine itself and the other as a generator, in the second part, states raised the theoretical basis of fractional calculus and fractional PID controller design and in the third part, was designed and implemented fractional PID control algorithms and conventional PID controller for motor-generator and performance system is compared. The results indicate that the fractional PID controller can be a good option for control of industrial processes.

Key words: control system, PID fractional, NINTEGER, identification, engine-generator.

1. INTRODUCCIÓN

Este artículo se ha estructurado desde los fundamentos y definiciones básicas del control fraccionario hasta las estrategias de implantación de controladores, incluyendo la identificación del sistema y el diseño de los controladores.

El cálculo fraccionario es la extensión del cálculo que permite considerar la integración y la derivación de cualquier orden, no necesariamente entero. En el dominio del tiempo, los operadores derivada e integral fraccionarios vienen definidos por la operación de convolución, por lo que están especialmente indicados para describir fenómenos de memoria. En el dominio de Laplace, dichos operadores se corresponden con el operador s^α, α ∈ R. El uso de controladores del tipo PID fraccionarios permite, frente al PID convencional, la aplicación de hasta cinco especificaciones de diseño, ya que cuentan con cinco parámetros a sintonizar. El método de sintonía propuesto se basa en especificaciones de frecuencia de cruce de ganancia, margen de fase, robustez ante cambios en la ganancia de la planta, restricción en la función de sensibilidad y rechazo al ruido de alta frecuencia.

El objetivo del trabajo es diseñar controladores PI y PID fraccionarios para controlar la velocidad de un motor de DC utilizado para manejar un generador de energía y comparar su desempeño con el de controladores PI y PID convencionales utilizando el método del lugar geométrico de las raíces (LGR). El empleo de los controladores fraccionarios en aplicaciones industriales está en etapa de desarrollo de ahí la importancia de este trabajo. En Romero (2010), se presenta la aplicación de las herramientas de cálculo fraccionario al control predictivo basado en modelos, con la idea de extender la metodología y generalizar su formulación, de tal forma que se puedan conjugar las ventajas de ambas disciplinas. Von Borries (2012) analizó la estabilidad y realizó simulaciones de un sistema adaptable basado en el Modelo de Error, usando leyes de ajuste con la derivada fraccionaria de Caputo de orden α ∈ (0 , 1], estudiando primero el caso escalar y luego, el caso vectorial. Johnson (2010) implementa y evalúa comparativamente tres estrategias de control: Control PI Tradicional, Control PI Fraccionario (FOPI) y Control adaptativo por modelo de referencia (MRAC). La implementación se realizó en un controlador industrial NI compact Field Point programado en ambiente LabView. Hernández (2013), modela el sistema de combustión de un horno cementero rotatorio de proceso húmedo, utilizando un balance de energía y una identificación de orden fraccionario y diseña un controlador de orden fraccionario en combinación con un método específico para hallar las ganancias proporcionales usando LQR Linear Quadratic Regulator.

2. MATERIALES Y MÉTODOS

2.1 Descripción del sistema motor-generador

El sistema implementado cuenta con dos motores de corriente continua de 24V. El primero se utiliza propiamente como motor y el segundo, movido por el primero, trabaja como generador, se desea controlar el voltaje generado.

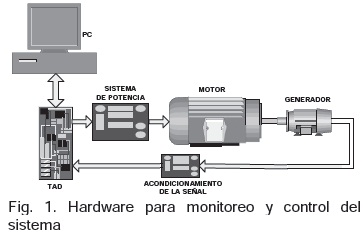
El hardware para el sistema de monitoreo y control del sistema está dispuesto como se indica en la figura 1 y lo constituyen los siguientes elementos:

• Tarjeta de adquisición de datos: P-TAD S01 BASIC-USB DAQ Multifunción, 10 bits, 25kS/s con 8 entradas análogas de 0 a 5v dos salidas análogas de 0 a 5V, 7 salidas digitales y 8 entradas digitales

• Sistema de acondicionamiento de la señal: toma el voltaje de salida del generador de 12V y lo convierte en señal de 0 a 5V

• Sistema de potencia: realiza la interfaz entre la tarjeta de adquisición de datos y el motor. Recibe señal de entrada de 0 a 5V y da una salida de 0 a 24V y 3A

• Computador.

• Generador: da una salida máxima de 24 VDC

• Motor de DC: alimentación de 24 VDC

2.2 Respuestas del sistema a la señal escalón.

La figura 2 muestra la respuesta del sistema correspondiente al voltaje producido por el generador, este voltaje es proporcional a la velocidad de giro del motor y, por esta razón, es la variable que permite realizar el control de la velocidad. Para obtener la dinámica del sistema se analiza la respuesta correspondiente a cada escalón y se obtienen modelos de primer orden con retardo. Los modelos obtenidos se validan y, finalmente se promedian sus parámetros para obtener el modelo definitivo.

2.3 Identificación del sistema motor-generador.

A continuación se presentan las respuestas individuales correspondientes a cada uno de los escalones. A la respuesta de cada escalón se le hizo una traslación de ejes con el fin de referenciar a cero las señales y facilitar el proceso de identificación. Esto se puede observar en las figuras 3, 4, 5 y 6. Para la identificación se utilizó el tolboox IDENT de MATLAB.

La identificación del sistema a partir de este escalón dio como modelo:

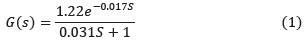
La identificación del sistema a partir de este escalón dio como modelo:

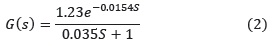
La identificación del sistema a partir de este escalón dio como modelo:

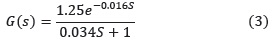
El modelo correspondiente a este escalón es: Planta de primer orden:

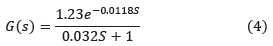
Con los modelos obtenidos se estima un modelo promedio cuya discretización con un periodo de muestreo T = 0.01 s da como resultado:

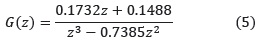
2.4 Controladores PID fraccionarios

En la actualidad, los controladores industriales sólo permiten la ejecución de tres acciones básicas de control, a saber: Proporcional (P), Integral (I) y Derivativa (D) y con estas se pueden obtener controladores P, PD, PI o PID. En este trabajo se presenta la generalización de las anteriores acciones básicas de control. Esta generalización se logra utilizando operadores integro-diferenciales de orden fraccionario para obtener las acciones Derivativa e Integral de orden no entero. Al realizar esta generalización, además de los tres parámetros de ajuste de que disponen los controladores PID clásicos (la ganancia proporcional Κ_p, y las ganancia integral y derivativa, Κ_i y Κ_d), se añade la posibilidad de ajustar el orden de integración (λ) y de la derivada (µ), con lo que se incrementa en dos el número de parámetros susceptibles de ajuste.

El controlador PID fraccionario se formula como:

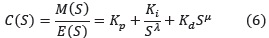
En la figura 7 se muestra la región de trabajo de un controlador PI^λD^µ fraccionario. Si λ = 1 y µ = 1 se tendrá el controlador PID convencional

2.5 Sintonía de los controladores PID fraccionarios

• Ajuste mediante el Método de respuesta en frecuencia: este método de sintonía propuesto para estos controladores se basa en establecer especificaciones de frecuencia de cruce por cero ω_c, margen de fase φ_PM, robustez ante cambios en la ganancia de la planta, restricción en la función de sensibilidad y rechazo al ruido de alta frecuencia. Este método calcula, mediante un algoritmo iterativo, el valor de los parámetros del controlador que minimiza estas cinco funciones. Este problema de minimización no lineal se ha resuelto empleando la función fmincon de Matlab (Matlab 2013) y (Monje, 2004)

Los ajustes se realizan con el cumplimiento de las siguientes especificaciones:

1. La ganancia a la frecuencia de cruce de ganancia ω_c debe ser igual a 1 es decir 0 dB

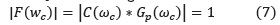
2. El Margen de fase φ_PM debe ser constante con valor:

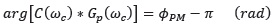
3. Rechazo al ruido en alta frecuencia ω_h en lazo cerrado debe ser

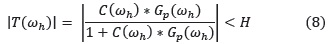
En donde T es la función de sensibilidad complementaria y H es la atenuación del ruido deseada para frecuencias mayores que ω_h

4. Rechazo de perturbaciones de la salida en lazo cerrado

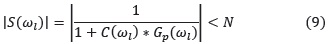
En donde N es el valor deseado para la función de sensibilidad S para frecuencias menores que ω_l

5. Robustez ante variaciones en la ganancia de la planta

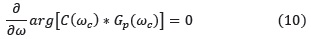
En todas las expresiones anteriores C(S) representa la función de transferencia del controlador y G_p(S) representa la de la planta.

La función a minimizar es:

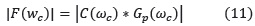
• Ajuste por tablas o Reglas de ajuste: existen tablas con reglas de ajuste como las que se han propuesto para los controladores PID enteros. Éstas han sido obtenidas previamente mediante optimización fijando los valores de los parámetros para plantas del primer orden con retardo (POR) y obteniendo los cinco parámetros que definen al PID fraccionario. En (Valério, 2005) se pueden encontrar varias tablas resumen de estos valores de ajuste para el PID en función de sus parámetros. La gran utilidad de estas tablas es que pueden ser aplicadas incluso sin disponer del modelo exacto de la planta a controlar.

3 RESULTADOS

3.1 Diseño del controlador PID fraccionario

El modelo promedio de la planta dio como resultado:

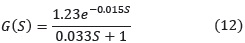
La figura 8 corresponde al diagrama de bode del sistema sin el controlador y de ella se obtiene que: φ_PM = 10.5 dB, MG = 126°, ω_c = 22 rad/s y ω_π = 120 rad/s.

Condiciones de diseño: Para el cálculo del controlador PI^λD^µ, se asumen las siguientes condiciones:

• Función a minimizar:

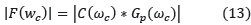
• La ganancia a la frecuencia de cruce de ganancia ω_c es igual a 1 (0 dB)

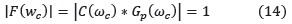
• Margen de fase φ_PM debe ser de 60° (1.047 rad)

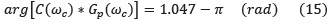
• Rechazo al ruido en alta frecuencia (ω_h = 10ω_C) menor de 20 dB (<0.01)

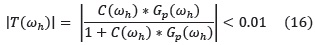
Rechazo de perturbaciones de la salida (ω_l = 0.1ω_C) menor de 20 dB (<0.01)

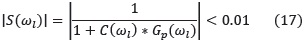
En todas las expresiones anteriores C(S) representa la función de transferencia del controlador y G_p(S) representa la de la planta.

Haciendo s = iω_c = 22 * i en la ecuación del controlador y en la función de transferencia del proceso y asumiendo µ = 0.6 se obtiene:

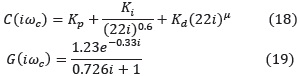
De la ecuación (19) se deduce qué: |G(iω_c)| = 1 y ∠ G(iω_c) = –36.3° = 0.633 rad.

Haciendo S = iω_h = 220 * i en la ecuación del controlador y en la función de transferencia del proceso y asumiendo µ = 0.6 se obtiene:

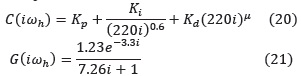
De la ecuación (21) resulta: |G(iω_h)| = 0.167 y ∠G(iω_h) = –54.8° = –0.957 rad.

Haciendo S = iω_l = 2.2 * i en la ecuación del controlador y en la función de transferencia del proceso y asumiendo µ = 0.6 se obtiene:

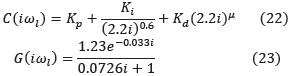
De la ecuación (28) se obtiene: |G(iω_l)| = 1.23 y ∠ G(ω_l) = 6° = 0.105 rad.

Combinando adecuadamente las ecuaciones 13 a 23 se obtienen las expresiones que conforman la función que se debe minimizar y las restricciones impuestas para dicha minimización. Al resolver las ecuaciones resultantes utilizando la función fmincon se obtienen los parámetros del controlador PI^λD^µ.

Función a minimizar:

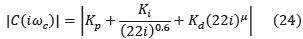
Restricciones:

• Ganancia a la frecuencia de cruce de ganancia ω_c:

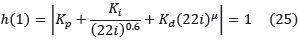
• Margen de fase de 60° (1.047 rad) φ_PM = π + ∠G(iω_c) + ∠ C(iω_c) de acá se deduce que ∠ C(iω_c) = –65.2° = –1.137 rad

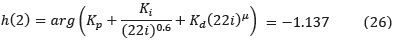
• Rechazo al ruido en alta frecuencia (ω_h = 10ω_C) menor de 20 dB (<0.01)

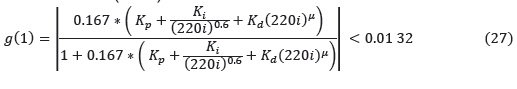
• Rechazo de perturbaciones de la salida (ω_l = 0.1ω_C) menor de 20 dB (<0.01)

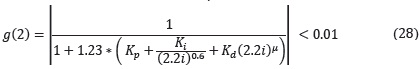
Como puede verse, la definición del problema consta de una función a minimizar, dos igualdades y dos desigualdades, elementos suficientes para estimar los cuatro parámetros del controlador: Κ_p, Κ_i, Κ_d y λ necesarios para minimizar la función de costo.

El controlador estimado en Matlab con la función fmincon es:

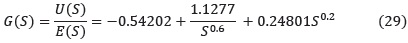
En el toolbox de control fraccionario denominado ''NINTEGER'' (Valerio 2011), se proporcionan las herramientas necesarias para transformar el controlador PID fraccionario en una función de transferencia con potencias de S enteras utilizando el comando nipid el cual tiene la siguiente sintaxis:

C= nipid(kp,kd,u,ki,lan,[ancho de banda],n, 'fórmula')

En donde:

kp, kd, u ,ki, lan: son los parámetros del controlador.

[ancho de banda]: es el ancho de banda especificado para el controlador.

n: El número de ceros y polos de la aproximación.

'fórmula': es el tipo de aproximación utilizada. Por ejemplo 'crone' para sistemas continuos ó 'tustin' para sistemas discretos.

El código que se da a continuación permite obtener controladores continuos y/o discretos a partir de un controlador PI^λD^µ fraccionario:

clc
% Aproximación entera del controlador PID
fraccionario
kp=-0.54202;
ki=1.1277;
kd=0.24801;
lan=0.6;
u=0.2;
cc=nipid(kp,kd,u,ki,lan,[2 200],2,'crone')% Continuo
cd=nipid(kp,kd,u,ki,lan,0.01,'tustin') %Discreto

Como resultado se obtienen las siguientes funciones de transferencia:

Controlador PID continuo equivalente:

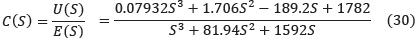
Controlador PID discreto equivalente con T = 0.01 :

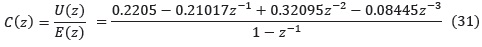
3.2 Controlador PI fraccionario con ajuste por tablas.

Teniendo en cuenta los parámetros del proceso Κ = 1.23, τ = 0.033 y θ = 0.015 , los ajustes del controlador son:

Por lo tanto, el controlador PI^λ es:

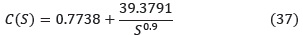
El sistema se simuló con este controlador y se obtuvo una respuesta rápida, estable pero con sobreimpulso muy alto (>40%), por lo que se hace uso de la sugerencia propuesta en (Chen 2007), con lo cual el controlador definitivo queda así:

Controlador PI discreto equivalente con T = 0.01 :

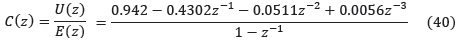
3.3 Diseño del controlador PID convencional

Para diseñar controladores PI o PID utilizando el Lugar Geométrico de la Raíces es necesario que el polo asignado cumpla dos condiciones: la condición de modulo y la condición de ángulo.

Condición de módulo:

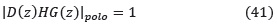
Condición de ángulo:

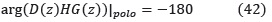
• Diseño del controlador PI convencional. Para un controlador PI discreto la función de transferencia se puede escribir como:

La función de transferencia discreta del sistema con T = 0.01 es:

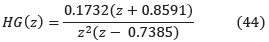
La función de transferencia en lazo abierto del proceso está dada por:

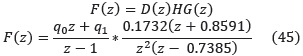
El tiempo de establecimiento del sistema en lazo abierto es t_s = 0.132 . Para realizar el diseño del controlador se asume que el tiempo de establecimiento del sistema en lazo cerrado es t_sLC = 0.1025 y que el coeficiente de amortiguamiento es ξ = 0.8

Las condiciones de diseño establecidas ubican el polo dominante de lazo cerrado deseado en z = 0.6488 ± j0.1949. Este polo debe cumplir la condición de módulo y la condición de ángulo, es decir:

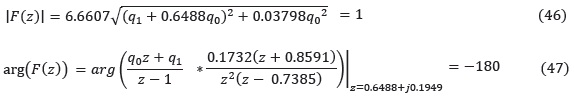
Resolviendo simultáneamente las ecuaciones (46) y (47) se obtiene: q₀ = 0.7152 y q₁ = –0.5198

Así el controlador PI es:

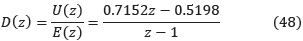
• Diseño del controlador PID convencional. Utilizando el método del lugar geométrico de las raíces y con polos ubicados en z = 0.6488 ± j0.1949 se diseñó un controlador PID discreto de modo que se cumplieran la condición de módulo y la condición de ángulo. Como este controlador tiene tres parámetros

• por ajustar, se adicionó una tercera condición haciendo que: q₂ = –0.25q₁ . El resultado del diseño dio el siguiente controlador PID:

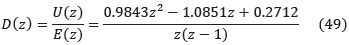
4 DISCUSIÓN

Implementación de los controladores PID fraccionario y PID convencional en el sistema real

Para implementar los controladores fraccionarios se hizo uso del toolbox NINTEGER de Matlab desarrollado por Valério (Valério 2011). La figura 9 muestra el diagrama en bloques utilizado para realizar el control con Simulink.

El bloque nipid corresponde al controlador fraccionario, el bloque Analog output es el bloque para la escritura de datos, el bloque analog input es el bloque de lectura de datos, éstos dos bloques se utilizan para realizar la comunicación entre la planta y el computador mediante la tarjeta de adquisición de datos. El bloque PTAD INIT habilita la tarjeta para su funcionamiento y, finalmente el bloque PTAD-SCOPE permite visualizar las variables que intervienen en el proceso.

Resultados obtenidos con el controlador PI y PID fraccionarios

Se calculó un controlador PID fraccionario utilizando la función fmincon de Matlab y un controlador PI fraccionario utilizando ajuste por tablas. El cálculo de estos controladores se presentó en el apartado anterior.

La figura 10 corresponde a la respuesta del sistema con el controlador fraccionario implementado directamente en simulink utilizando el toolbox Ninteger.

Se observa que el sistema se estabiliza con error promedio cero, sin sobreimpulso y la acción de la ley de control sobre el elemento final de control es suave y sin oscilaciones significativas.

En la figura 11 se presenta la respuesta del sistema con el controlador PID fraccionario en su forma equivalente de potencias en S enteras la cual se obtuvo mediante el comando nipid y la opción crone. Al igual que con el controlador PID Fraccionario original, la respuesta del sistema es estable, sin sobreimpulsos y con error promedio cero, la diferencia radica en que este es más lento presentando mayor tiempo de establecimiento.

La figura 12 corresponde a la respuesta del sistema con el controlador PID fraccionario en su forma equivalente de potencias en z enteras la cual se obtuvo mediante el comando nipid y la opción tustin. La respuesta no presenta sobreimpulso tiene error cero en estado estable, menor tiempo de establecimiento que los casos anteriores y el trabajo de la ley de control sobre el elemento final de control es suave y sin oscilaciones considerables.

La figura 13 muestra el comportamiento del controlador PI fraccionario diseñado mediante ajuste por tablas. Se observa una respuesta sin sobreimpulsos, con error de estado estable igual a cero y tiempo de establecimiento pequeño. La acción sobre el elemento final de control es suave.

La figura 14 corresponde a la respuesta con el controlador PI fraccionario continuo equivalente. Esta respuesta presenta características similares a las del PI fraccionario original, aunque se observa una mayor sensibilidad en la respuesta que se traduce en pequeñas oscilaciones como se aprecia en la figura.

La figura 15 corresponde a la respuesta del sistema con el controlador PI fraccionario en su forma equivalente de potencias en z enteras la cual se obtuvo mediante el comando nipid y la opción tustin. El sistema presenta muy buena velocidad de respuesta, no presenta sobreimpulso tiene error cero en estado estable, y el trabajo de la ley de control sobre el elemento final de control es suave y sin oscilaciones considerables.

Resultados obtenidos con el PI y PID convencionales

La figura 16 muestra la respuesta del sistema con el controlador PI discreto convencional estimado utilizando el método del LGR y asignación de polos. Se puede observar que el sistema tiene muy buena velocidad de respuesta, sin sobreimpulso, con error de estado estable igual a cero y la acción de la ley de control sobre el elemento final es adecuada.

En la figura 17 se muestra la respuesta del sistema con el controlador PID Discreto Convencional estimado utilizando el método del LGR y asignación de polos. Se puede observar que el sistema tiene muy buena velocidad de respuesta, sin sobreimpulso, con error de estado estable igual a cero y la acción de la ley de control sobre el elemento final es adecuada.

Comparación del desempeño en el proceso real Para comparar el desempeño obtenido en la simulación con los diferentes controladores diseñados se utilizaron diferentes métricas con el fin de establecer suficientes criterios de análisis y tener elementos cuantitativos y cualitativos para realizar la comparación.

Se analizan criterios de respuesta temporal como el tiempo de establecimiento, el máximo sobreimpulso y el error de estado estable, criterios de la integral del error como IAE, IAET, ICE e ICET y criterios de respuesta en frecuencia como el margen de ganancia y el margen de fase. En la tabla 1 se muestran los valores obtenidos con los diferentes criterios de comparación.

Los resultados indican que los controladores que presentan el mejor desempeño en cuanto a las métricas de respuesta temporal son el PIDE (PI fraccionario en su forma equivalente de potencias en z enteras) y el PI discreto diseñado mediante el método del LGR, mientras que en este aspecto los de peor desempeño son el PIDCE (PID fraccionario en su forma equivalente de potencias en S enteras) y el PICE (PI fraccionario en su forma equivalente de potencias en S enteras).

En cuanto a los criterios de error los de mejor desempeño son el PID y el PI discretos diseñados con el método del LGR.

En términos generales, se observó que el desempeño de los controladores discretos fue mejor que el de los controladores continuos, esto es un indicativo de la versatilidad de los controladores digitales y de su eficiencia al momento de regular un proceso.

Algunos autores como Ortiz y Cardona (2009) quienes diseñaron un control PID tipo fraccional para la posición del cabezal de una unidad de CD utilizado en el desarrollo de un microscopio óptico motorizado y Barbosa (2011) que compara el desempeño de un controlador PID adaptativo y de un controlador PID fraccionario para controlar la posición del vástago de un cilindro lograron un sistema de respuesta rápida, sin sobreimpulso y con una precisión aceptable, resultados comparables con los obtenidos en el presente trabajo.

5 CONCLUSIONES

• Se aplicaron las bases teóricas del cálculo fraccionario y del diseño de controladores PID fraccionarios y se demostró que estos controladores son una buena opción en el control de procesos.

• Se implementaron los algoritmos para el control PID fraccionario y PID convencional de acuerdo a la metodología de estudio establecida, arrojando resultados satisfactorios en el comportamiento del sistema.

• Con cualquiera de las estrategias de control aplicadas se obtiene un buen seguimiento de referencia de la velocidad del motor, con un comportamiento estable y operando de forma adecuada para una condición de operación particular. Con los controladores lineales PI clásico y PI fraccionario resulta factible conseguir respuestas muy buenas en términos de velocidad de respuesta, tiempo de establecimiento y máximo sobreimpulso.

• El PI fraccionario presenta ventajas frente al PI clásico, pues posee un grado de libertad más que el primero, permitiendo así ajustar a voluntad aún más características de la respuesta.

• Se aplicaron métodos de sintonía generales en el dominio de la frecuencia para los reguladores de orden fraccionario que garantizan el cumplimiento de las especificaciones de respuesta en frecuencia: frecuencia de cruce de ganancia (velocidad del sistema) y margen de fase (sobreimpulso).

• Se han tenido en cuenta en el diseño de controladores fraccionarios otros parámetros que mejoran el desempeño de los controladores como son la sensibilidad ante ruidos y perturbaciones cosa que no se puede hacer en la sintonía de los controladores PID convencionales.

• Se implementaron los sistemas de control PID fraccionario y PID convencional en el sistema real, ambos controladores arrojaron un resultado satisfactorio en control de la salida de generación de energía. Al comparar el desempeño del controlador fraccionario con el control PID convencional por el método del lugar de las raíces se concluyo que ambos presentan un buen desempeño.

6 AGRADECIMIENTOS

Nuestro agradecimiento al Politécnico Colombiano Jaime Isaza Cadavid por el acompañamiento y suministros de implementos que permitieron llevar a cabo este trabajo.

7 REFERENCIAS

[1] Barbosa, L. Control fraccionario y adaptativo de un cilindro neumático. Proyecto fin de carrera. Escuela Politécnica Superior de la Universidad Carlos III de Madrid. 2011.

[2] Chen (2007). Practical Tuning Rule Development for Fractional Order Proportional and Integral Controllers. Journal of computational and nonlinear dynamics. Las Vegas. 2007.

[3] Franklin et al. Feedback Control of Dynamic Systems. 4^a Edición, New Jersey. Ed. Prentice Hall. 2002.

[4] García. Control Digital. Teoría y práctica. Politécnico Colombiano JIC. Medellín. Tercera Edición. ISBN 978-958-44-8641-7. 2011.

[5] Hernández, O. Metodología para modelar y controlar un sistema de combustión utilizando cálculo fraccional. Tesis. Instituto Tecnológico Metropolitano. Facultad de Ingenierías. Maestría en Automatización y Control Industrial Medellín. 2013.

[6] Johnson, V. Diseño e implementación de estrategias de control avanzado sobre plataforma Labview para un sistema de calentamiento inductivo de fluidos. Tesis de grado. Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Eléctrica. Santiago De Chile. 2010.

[7] Matlab. The MathWorks. MATLAB Documentation, 9 edition. 2010.

[8] Matlab. Optimization Toolbox™ User's Guide© COPYRIGHT 2013 by The MathWorks, Inc. 2013.

[9] Monje, C.A., Vinagre, B.M., Chen, Y.Q., Feliu, V., Lanusse, P., Sabatier, J., ''Proposals for fractional PI^λD^µ tuning'', FDA'04. pp. 156-161, Bordeaux, France. 2004.

[10] Oldham, K.B. y J. Spanier. The Fractional Calculus. Academic Press, New York. 1974.

[11] Ortiz, P y Cardona, L. Control PID tipo fraccional para la posición del cabezal de una unidad de CD para aplicaciones en microscopia óptica. ITECKNE Vol. 9 Número 2 ISSN 1692 – 1798. 2012.

[12] Podlubny, I. Fractional-Order Systems and PI^λD^µ Controllers. IEEE Transactions on Automatic Control 44 N° 1 Pp 208-214. 1999.

[13] Romero, H.M. Control Predictivo de Orden Fraccionario. Tesis Doctoral. Universidad Nacional de Educación A Distancia. Madrid. 2010.

[14] Sauchelli, V. H, Laboret, S. Cálculo Fraccional Aplicado a Control Automático. Mecánica Computacional. Volúmen X XVI, pp3308-3327. Córdoba, Argentina. 2007.

[15] Saxena, et al. ''On Fractional Kinetic Equations.'' http://arxiv.org/abs/math.CA/0206240. 2002.

[16] Valério, D. Fractional robust system control. PhD thesis. Instituto Superior Técnico, Lisboa (Portugal). 2011.

[17] Valério. Ninteger v. 2.3 Fractional control toolbox for MatLab. Universidad Técnica de Lisboa Instituto Superior Técnico. 2011.

[18] Von Borries, M. Estudio y Simulación de Sistemas Adaptables Fraccionarios. Tesis de Maestría. Universidad de Chile Facultad de Ciencias Físicas y Matemáticas. Departamento Ingeniería Eléctrica. Santiago de Chile. 2012.