ARTÍCULOS

METODOLOGÍAS DE OPTIMIZACIÓN APLICADAS A LA COORDINACIÓN ÓPTIMA DE PROTECCIONES DE SOBRECORRIENTE

OPTIMIZATION METHODOLOGIES APPLIED TO THE OPTIMAL COORDINATION OF OVERCURRENT RELAYS

Johnathan Zapata Castro¹, Jesús María López Lezama²

1 Estudiante de Maestría en Ingeniería, Grupo GIMEL, Departamento de Ingeniería Eléctrica, Facultad de Ingeniería, Universidad de Antioquia UdeA, Calle 70 No 52–21, Medellín, Colombia.

2 Ph.D. en Ingeniería Eléctrica, Grupo GIMEL, Departamento de Ingeniería Eléctrica, Facultad de Ingeniería, Universidad de Antioquia UdeA, Calle 70 No 52–21, Medellín–Colombia. E–mail: jesusmarialopezl@gmail.com

Recibido: 04 de Mayo de 2014. Aceptado: 30 de Junio de 2014.

RESUMEN

La coordinación de relés de protección en los sistemas eléctricos de potencia (SEP) es una de las tareas más importantes y dispendiosas, debido al impacto de una mala operación por descoordinación y a la cantidad de información que se debe procesar. En este artículo se presenta una revisión del estado del arte en la coordinación de relés de sobrecorriente. También se presentan algunas de las consideraciones a tener en cuenta para el empleo de protecciones adaptativas y varias de las metodologías que se han desarrollado desde la modelación matemática, hasta el uso de sistemas de inteligencia artificial para la coordinación de relés de sobrecorriente. Entre los métodos estudiados se encuentran: programación lineal, algoritmos evolutivos, algoritmos genéticos, optimización mediante colonia de partículas y algoritmos de colonias de abejas. Se presentan gráficos y tablas mostrando la evolución de las diferentes técnicas empleadas para abordar el problema de coordinación óptima de protecciones de sobrecorriente.

Palabras clave: Coordinación de relés de sobrecorriente, Computación evolutiva, Inteligencia artificial.

ABSTRACT

Coordination of protection relays is one the most important and time consuming tasks in power systems due to the consequences that a lack of coordination might cause, and to the amount of information that must be processed. A review of the state of the art on overcurrent relay coordination is presented as well as some considerations to be taken into account in the use of adaptive protections and several methodologies that have been developed from the mathematical modeling to the use of artificial intelligence for the coordination of overcurrent relays. Among the discussed methods are: linear programming, evolutionary algorithms, genetic algorithms, particle swarm optimization and artificial bee colony algorithms. Several figures and tables are shown to depict the evolution of different techniques applied to the optimal overcurrent relay coordination problem.

Key words: Overcurrent relay coordination, Evolutionary computation, Artificial intelligence.

1. INTRODUCCIÓN

Con la implementación y desarrollo de los mercados de energía, los sistemas de potencia son forzados a operar en condiciones cercanas a sus límites, siendo necesario mantener la prestación del servicio continuo, confiable y de calidad [1]. Diversos estudios han identificado que la mayoría de los apagones (blackouts) en los sistemas de potencia se deben, en gran medida, a un desempeño inapropiado de los relés de protección. Dejando a un lado las fallas ocultas en los relés de protecciones, un factor importante de las desconexiones es el inapropiado ajuste de los relés a las condiciones actuales del sistema [2] y [3]. Durante la operación de un sistema de potencia interconectado pueden ocurrir condiciones anormales. Tales condiciones pueden causar interrupción de la alimentación y daños en los equipos conectados al sistema [4]. Un aspecto importante a tener presente en la operación de un sistema de potencia es que cualquier falla debe ser despejada oportunamente por los sistemas de protección en el menor tiempo posible con el mínimo de desconexión de elementos, de ahí la necesidad de una correcta coordinación de los diferentes tipos de relés de protección [5].

Para asegurar la confiabilidad de los sistemas de protección, el esquema de respaldo no puede entrar en operación hasta que el sistema principal falle. En otras palabras, debe operar después de cierto retardo conocido como intervalo de tiempo de coordinación, dando la oportunidad a la protección principal de operar. Antes de 1970, la coordinación de protecciones era realizada por un ingeniero de protección, con la ayuda de herramientas de cálculo especiales [6] donde casi siempre los métodos aplicados no eran óptimos debido a la aplicación de su filosofía personal y experiencia práctica [7]. Con el desarrollo de los computadores personales y gracias a su capacidad de procesamiento y memoria se ha automatizado este proceso a una filosofía de solución iterativa, donde el ingeniero ejecuta diferentes casos, para diferentes fallas y configuraciones, hasta que una solución aceptable es alcanzada [8]. Este proceso se ha convertido en uno de los principales temas de investigación de la industria de los relés de protección y campos de investigación relacionados. En la última década, se ha desarrollado un gran número de metodologías para la optimización de la coordinación de relés de sobrecorriente. Tales metodologías se basan en técnicas de programación lineal como el método simplex o métodos de punto interior; también se han empleado técnicas de inteligencia artificial como algoritmos genéticos, redes neuronales y lógica borrosa (fuzzy logic) [9] y [10], colonia de partículas, sistemas expertos y razonamiento basado en modelos con resultados satisfactorios [11], [12].

En las referencias [13] – [15] se presentan algunas de las técnicas de inteligencia artificial que están siendo actualmente empleadas para implementar estrategias de protección adaptativas en sistemas eléctricos de potencia.

En este artículo se presentan las principales técnicas empleadas para la optimización de la coordinación de relés de sobrecorriente, como también otros aspectos relacionados con la operación de estos. En la sección II se presenta el concepto de protecciones adaptativas, además de las ventajas y las desventajas del uso de la inteligencia artificial en estas. En la sección III se presenta el estado del arte de la coordinación de protecciones de sobrecorriente desde 1988 hasta el año 2014. En la sección IV se detalla el problema de la coordinación óptima de relés de sobrecorriente. En la sección V se plantea la coordinación óptima de relés de sobrecorriente direccionales mediante el empleo de técnicas de programación lineal. En la sección VI se presenta la coordinación de relés de sobrecorriente mediante técnicas de inteligencia artificial. Finalmente, en la sección VII se presentan las conclusiones.

2. PROTECCIONES ADAPTATIVAS

Los sistemas convencionales de protección responden a fallas o eventos anormales de una manera fija y predeterminada. Esta forma predeterminada, embebida en la característica de los relés, está basada en ciertas consideraciones acerca del sistema de potencia. Con el advenimiento de los relés digitales el concepto de responder a los cambios del sistema ha tomado una nueva dimensión. Los relés digitales tienen dos características importantes que los hacen vitales para el concepto de relés adaptables. Sus funciones son determinadas a través de software y su capacidad de comunicación [16].

Las protecciones adaptativas se definen formalmente como: ''una filosofía de protección la cual permite y busca realizar ajustes en varias funciones de protección automáticamente para hacerlas más sintonizadas a las condiciones actuales del sistema'' [2] y [16].

La necesidad de sistemas de protecciones ''inteligentes'' no es algo novedoso en los SEP (Sistemas Eléctricos de Potencia), es así como desde hace varios años se tienen sistemas de protección, por ejemplo, con la posibilidad de tener distintos grupos de ajustes, permitiendo de una manera ágil el cambio de estos ante distintas condiciones o topologías del sistema. En el marco de las redes inteligentes, en Colombia se han adelantado proyectos de investigación en el área de medición fasorial en el Sistema Interconectado Nacional (SIN), mediante el desarrollo inhouse de una PMU (Phasor Measurement Unit) para un prototipo WAMS (Wide Area Measurement Systems) usando un número limitado de PMU con combinación de fabricantes y el desarrollo de la PMU–XM [17]. Otro grupo de aplicaciones de la medición con PMU se caracteriza por aumentar la eficacia de la protección de los sistemas de transmisión de energía suministrando por ejemplo, el estado de determinados interruptores y seccionadores, el flujo de energía en líneas eléctricas fundamentales, las tensiones en barras críticas, la potencia de salida de los generadores clave, etc., de tal manera que puedan ser utilizados para formular una estrategia de respuesta al valor y estado de estos parámetros [18].

En [19] se propusieron cinco áreas de enfoque principales, de acuerdo con la estructura propia que compone el negocio eléctrico: Transmisión, Generación, Distribución, Comercialización y Áreas de Soporte; las protecciones adaptativas quedaron en el área: Transmisión / Sub área: Operación avanzada (inteligente) / Elemento: Protección adaptativa. En [9], [15] y [20] se presenta un estudio detallado de la literatura del problema de la coordinación de relés de sobrecorriente, allí se clasifican los trabajos previos en tres categorías: técnicas de ajuste de curvas, técnica de gráfica teórica y técnicas de optimización. Las técnicas y programas de inteligencia artificial pueden operar con los datos del sistema y aplicar reglas para calcular y realizar los ajustes necesarios de forma automática. Dentro de las metodologías de inteligencia artificial, aplicadas a la coordinación de relés de sobrecorriente se destacan:

º Lógica borrosa
º Razonamiento basado en modelos
º Redes neuronales artificiales (ANN)
º Razonamiento basado en casos
º Meta control
º Sistemas expertos
º Técnicas metaheurísticas

Vale la pena mencionar que la adaptación de ajustes como una función de una condición externa no es fundamentalmente un concepto nuevo. Por ejemplo, los esquemas de teleprotección existentes en los relés antiguos están basados en la adaptación de un ajuste como una función de una entrada de información externa [2].

2.1 Ventajas y desventajas del uso de inteligencia artificial

La aplicación de la inteligencia artificial en la ingeniería de protecciones es necesaria cuando hay incertidumbre y datos incompletos, y donde la aplicación es considerada más un arte que una ciencia. Si un conjunto de reglas y datos precisos pueden ser hallados para la práctica de ingeniería de protecciones, entonces no habría necesidad de la inteligencia artificial. El área de la lógica borrosa pretende principalmente modelar información imprecisa y razonamiento heurístico. La teoría de conjuntos borrosos se relaciona con clases de objetos de fronteras difusas en las cuales la pertenencia es de algún grado [21], mientras que las ANN pueden modelar aplicaciones que son difíciles de definir matemáticamente. Los sistemas expertos permiten el uso de reglas explícitas para construir una base de conocimiento, pero esas reglas y la salida de decisión pueden recaer en lógica borrosa para la interpretación de los datos. Una desventaja de los sistemas expertos es que algunas tareas son más exitosas que otras dependiendo de la población de la base de conocimiento [13]. Adicionalmente, es difícil construir un sistema experto que pueda capturar completamente la experticia de los expertos humanos. Algunas de las barreras para la adquisición de este conocimiento son: (i) es difícil para los expertos articular su experticia, (ii) la inhabilidad del ingeniero de conocimiento para realizar las preguntas pertinentes desde el dominio del ingeniero para extraer la información relevante y (iii) el temor de los expertos de pasar su experticia por el miedo a perder su importancia [21]. Los sistemas expertos no pueden reemplazar la necesidad de humanos expertos, quienes deben estudiar los problemas de sistemas de potencia, aplicar la experiencia pasada y aprender una nueva solución. Las ANN son buenas para la interpolación, pero no lo son en extrapolación. Puesto que las ANN exhiben las mismas propiedades que los sistemas biológicos, también sufren las mismas limitaciones. Para algunas tareas el cálculo secuencial es mejor que usar una ANN. La lógica borrosa posee mayores capacidades que sus contrapartes para capturar incertidumbre y puede capturar la vaguedad de las descripciones de entrada. Esto, en torno a la habilidad de modelar el razonamiento del sentido común humano, el diagnóstico, la toma de decisiones y otros aspectos del conocimiento humano [13].

3. ESTADO DEL ARTE DE LAS PROTECCIONES ADAPTATIVAS APLICADAS AL PROBLEMA DE LA COORDINACIÓN ÓPTIMA DE RELÉS DE SOBRECORRIENTE

Los relés de sobrecorriente aún son una buena selección técnica y económica para protección de sistemas de subtransmisión interconectados. Como se ha indicado anteriormente, es difícil resolver el problema de la coordinación mediante métodos de ensayo y error o mediante análisis topológico. Generalmente la coordinación de relés de sobrecorriente requiere la selección de la corriente de arranque o PSM (Plug Multiplier Setting) y el ajuste de dial de tiempo (TDS Time Dial Setting). Para una coordinación óptima, estos parámetros deben ser ajustados para satisfacer todas las restricciones con el menor tiempo de operación de los relés de protección [22].

En la última década, se han desarrollado un gran número de metodologías para la optimización de la coordinación de relés de sobrecorriente. Los métodos empleados hasta ahora pueden ser clasificados en las siguientes categorías [23]:

• Análisis topológico (punto de quiebre – BP, esquema de descomposición de configuración)

• Programación lineal (programación lineal – PL, simplex, simplex de dos fases, programación lineal entera mixta y puntos interiores)

• Programación no lineal

• Metaheurísticas (algoritmos evolutivos – AE, algoritmos genéticos – AG, colonia de partículas – PSO, colonia artificial de abejas – ABC Artificial Bee Colony, algoritmo luciérnaga – AL, etc.)

• Otros (métodos gráficos, optimización de restricciones – OR, sistemas expertos – SE, inteligencia artificial – IA, modificación de la corriente de arranque, detección de escenarios, programación secuencial cuadrática – SQP, etc.)

En los últimos años se ha observado un leve incremento en las publicaciones sobre el empleo de diferentes técnicas para la solución de problemas de optimización mediante técnicas como la programación lineal, el uso de la inteligencia artificial y en especial su aplicación al campo de la optimización de la coordinación automática de protecciones de sobrecorriente.

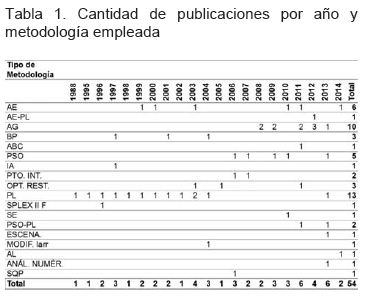
La cantidad de publicaciones por tipo de metodología empleada (consultadas principalmente en las bases de datos de IEEE Explore y Science Direct) para la solución del problema de la coordinación óptima de relés de sobrecorriente se consigna en la Tabla 1. Las distintas metodologías halladas para la solución del problema de la coordinación automática de relés de sobrecorriente, se agruparon en las siguientes cinco categorías:

• Análisis topológico – AT

• Metaheurístico – MH

• Programación lineal – PL

• Inteligencia artificial – IA

• Otros

De acuerdo a las cinco categorías definidas anteriormente, se agruparon las publicaciones en la Tabla 2. Se puede observar que desde el inicio del planteamiento de la coordinación de protecciones de sobrecorriente como un problema de optimización en 1988 (por Urdaneta) hasta 2014, se han empleado diversas técnicas metaheurísticas como método de solución de dicho problema.

En los últimos tres años se ha encontrado la mayor cantidad de publicaciones sobre el tema de la coordinación óptima de relés de sobrecorriente tal como se aprecia en la Figura 1, observándose un aumento en los últimos años en investigación sobre el tema.

En la Figura 2 se presenta la distribución de las metodologías empleadas, donde se destaca el uso de las metaheurísticas.

De la Figura 3 se logra establecer que las principales metodologías empleadas para la coordinación automática de relés de sobrecorriente son la programación lineal y los algoritmos genéticos.

Algunas de las metodologías de tipo topológico se basan en la determinación de puntos de quiebre (BP break points) [6], [7] y [24]. Los BPs son localizaciones deseadas de inicio del procedimiento de coordinación y son usados para reducir el número de iteraciones en el proceso de coordinación. Las técnicas de optimización han simplificado la filosofía de coordinación de protecciones y debido a sus ventajas inherentes tienen gran popularidad. Su principal ventaja es la eliminación de la necesidad de determinar el conjunto de puntos de quiebre y por esta razón, no es requerido un programa de análisis topológico elaborado y complejo [15].

En las referencias [22], [25] y [26] no se construye una función objetivo a ser optimizada, si no que se hallan los ajustes óptimos de los relés de sobrecorriente resolviendo directamente las ecuaciones de las restricciones basados en las reglas de optimización. Adicionalmente en [26] se presenta un método para reducir el número de restricciones y detectar aquellas que hacen la optimización de los ajustes de los relés de sobrecorriente no factible. En [27] se presenta una metodología para la coordinación de relés de sobrecorriente en SEP con generación distribuida, de tal manera que se mejora el alcance de los relés de sobrecorriente modificando el ajuste de la corriente de arranque cuando la generación distribuida está o no conectada al sistema.

Dentro de las técnicas de optimización se han empleado programación lineal con método simplex, simplex de dos fases y simplex dual [5], [8], [24], [28] – [40], también se han empleado técnicas de inteligencia artificial como algoritmos evolutivos [41] – [46], algoritmos genéticos [11], [12] , [22] y [47] – [54], redes neuronales [9], lógica borrosa (fuzzy logic) [9], colonia de partículas [4], [55] – [60], colonia artificial de abejas [61], programación cuadrática secuencial (SQP) [62], algoritmo luciérnaga (firefly algorithm – FA) [63], sistemas expertos [64], algoritmos numéricos [65] y razonamiento basado en modelos.

4. EL PROBLEMA DE LA COORDINACIÓN ÓPTIMA DE RELES DE SOBRECORRIENTE

Un relé de tiempo inverso típico consiste en dos elementos, una unidad instantánea y una unidad de sobrecorriente de tiempo inverso. La unidad de sobrecorriente tiene dos valores para ser ajustados, la corriente de arranque (Ip ó Iset) y el ajuste de dial de tiempo (TDS). El tiempo de operación del relé i , está dado por la ecuación (1)

Las constantes α y n dependen del dispositivo que se esté empleando y determinan el comportamiento de éste.

En la Tabla 3 se muestran las constantes de la ecuación (1) según norma IEC [66] para el cálculo del tiempo de operación de los relés de sobrecorriente de acuerdo con el tipo de curva.

Los relés ubicados en diferentes subestaciones, detectan las corrientes de falla de una manera diferente durante el instante en que ocurre la falla. El problema de la coordinación de relés es determinar la secuencia de operación de los relés para cada localización de falla posible, de tal manera que la sección fallada sea aislada para proporcionar suficientes márgenes de coordinación sin retardo de tiempo excesivo y de esta manera mejorar la confiabilidad del SEP. El cálculo de los dos ajustes TDS (ó TMS) e Ip, es la esencia del estudio de coordinación de relés de sobrecorriente direccional [8].

La planeación y operación de sistemas de potencia frecuentemente requiere la adición de nuevas ramas (por ejemplo líneas de transmisión, transformadores, etc), y modificaciones a la estructura del sistema con el fin de seguir las características variables de la carga. Esos cambios en la red de transmisión modifican la respuesta del sistema debido a condiciones de falla y por lo tanto, requieren la verificación y modificación continua de las características de los dispositivos de protección del sistema [28]. Debido a este cambio en la estructura de la red, no solo se requiere el ajuste de los nuevos relés, sino que implica el ajuste de los relés existentes con el fin de satisfacer las necesidades del sistema. La modificación de un gran número de ajustes es costoso e indeseable. Por lo tanto, una solución factible con tiempos de operación más altos pero con menos relés para ser reajustados puede ser preferida.

En [28] se presenta una serie de problemas de programación lineal de dimensión reducida, sacrificando parte de la optimización de la formulación original, tratando una solución subóptima con un tiempo de operación más alto pero con menos relés para ser ajustados.

5. COORDINACIÓN DE RELES DE SOBRECORRIENTE DIRECCIONAL USANDO PROGRAMACION LINEAL

La aplicación de programación lineal al procedimiento de coordinación de protecciones de sobrecorriente fue presentada por Urdaneta y Pérez en 1988 [8]. Este problema puede ser expresado de forma general como se indica en (2).

Donde z representa un índice de comportamiento adecuado, s representa los ajustes de protección, S es el conjunto de ajustes permitidos y p representa las perturbaciones o condiciones de falla. Este problema puede ser formulado como un problema de optimización no lineal de la forma (3):

Donde la característica de tiempo de operación del relé de sobrecorriente es una función no lineal de las variables dial de tiempo y corriente de arranque. Esta metodología tiene como finalidad encontrar los valores mínimos de dial para los relés de tiempo inverso, donde las corrientes de arranque y la relación de transformación son calculadas con anterioridad para encontrar las restricciones de coordinación. Con el cálculo de las corrientes de arranque como un factor de la corriente de carga o de la corriente nominal del circuito de transmisión, el problema llega a ser lineal y los únicos valores a encontrar corresponden a los diales de tiempo de cada relé [35].

Los relés de distancia son usados como protección principal y los de sobrecorriente como protección de respaldo. Para este tipo de esquemas se deben tener en cuenta dos clases de restricciones. Una es que el relé de sobrecorriente debe ser más lento que la segunda zona del relé de distancia asociado al interruptor principal. La otra restricción es que la zona dos del circuito de respaldo debe ser más lento que el relé de sobrecorriente direccional del interruptor principal [30]. En [31] se presenta un método para determinar automáticamente el tiempo óptimo para la segunda zona de los relés de distancia en un esquema combinado con relés de sobre corriente. En la referencia [34] se presenta una comparación del esquema de protección para un sistema interconectado 115/69 kV de la zona oriental de Venezuela, donde se consideran tres casos: a) coordinación independiente de los relés de tiempo inverso y los relés de distancia, b) coordinación combinada de los relés de tiempo inverso considerando los relés de distancia y c) coordinación conjunta ajuste de relés de sobrecorriente de tiempo definido de alta corriente. Se presentan las ventajas y desventajas de la aplicación de cada uno de los casos.

La mayoría de las técnicas de programación lineal están restringidas al uso de relés modernos con pasos de dial cercanos, de tal manera que tratan los TDS como variables continuas, como en [35], teniendo luego que ajustarse los valores de acuerdo con la resolución permitida por los relés que están siendo usados.

5.1 Coordinación de protecciones considerando cambios topológicos en la red

Los métodos actuales para el cálculo de los ajustes de relés de sobrecorriente pueden ser clasificados en dos grupos: las técnicas topológicas y las técnicas de optimización [29]. Es bien conocido que, en algunas situaciones, los cambios dinámicos en la topología de la red podrían hacer que el sistema de protección opere sin selectividad. Los relés podrían operar correctamente si el efecto de esas situaciones transitorias fueran tomadas en cuenta cuando se está realizando la coordinación de los relés.

Las consideraciones de cambios dinámicos en la configuración de la red, adicionará dos ecuaciones a cada par de restricciones de coordinación. Esto incrementará la dimensión del problema, la cual es de por sí muy grande sin considerar los cambios dinámicos. Este incremento en la dimensión del problema puede minimizarse si el sistema es analizado previamente.

En [52] se presenta una metodología para la determinación de los pares de relés principal y respaldo conociendo la topología del sistema en un grupo de matrices.

En [58] se aplica el método simplex Nelder–Mead y PSO para la solución del problema de coordinación de relés de sobrecorriente, este estudio considera una topología de red variable en estado estacionario en lugar de una red bajo estado transitorio como se explica en [29]. Las restricciones adicionales, tales como la falta de coordinación causados por grandes corrientes transitorias en los relés de respaldo de los pares de relés de protección resultantes de la desconexión de los relés cercanos, no son considerados en este estudio.

En [37] se resuelve el problema de la coordinación de relés de sobrecorriente direccional mediante programación lineal, teniendo en cuenta las restricciones asociadas a las configuraciones transitorias de la red presentadas durante el proceso de despeje de las fallas, asegurando la completa selectividad de la operación de los relés para el esquema de falla seleccionado. En [67] se presenta un esquema de coordinación de relés de sobrecorriente ante cambios en la carga, generación o topología de la red mediante la aplicación de programación lineal. En [68] se presenta una técnica en la cual se emplea simulación de tiempo real (RTDS), la metodología planteada consiste en determinar los diferentes escenarios debidos a cambios en la topología y para estos realizar el ajuste óptimo; de tal manera que mediante una supervisión continua del sistema se detecten los cambios en la topología y de esta manera activar el grupo de ajuste de los relés de acuerdo con el escenario detectado.

6. COORDINACIÓN DE RELES DE SOBRECORRIENTE DIRECCIONAL USANDO TÉCNICAS DE INTELIGENCIA ARTIFICIAL

El problema de optimización de coordinación de relés de sobrecorriente se ha resuelto mediante diferentes técnicas, durante los últimos años ha tenido gran auge el uso de las técnicas de inteligencia artificial. Entre los tipos de técnicas inspiradas por los métodos de selección natural que han sido empleadas se encuentran: las colonias de partículas, las colonias artificiales de abejas y el algoritmo luciérnaga entre otras. Estas técnicas han sido desarrolladas para obtener soluciones globales óptimas en tiempos de cálculo razonables.

En [47] se realiza la coordinación de relés de sobrecorriente mediante AG en un sistema de distribución para el caso lineal, adicionando las restricciones a la función objetivo con la finalidad de dejar el problema irrestricto. En [48] se emplean algoritmos genéticos para determinar el tiempo de operación de los relés para las funciones objetivos lineales y no lineales. Para la función lineal, el valor TDS es hallado para valores de corriente de arranque Ip dados, y para la función no lineal el valor de las corrientes de arranque Ip son obtenidos para unos valores de TDS. En [49] se plantea el algoritmo genético continuo CGA, donde las variables son representadas por números de punto flotante. En [50] se presenta una metodología en la cual, a parte de establecer los ajustes correspondientes a los relés de sobrecorriente, también permite determinar el tipo de característica de operación de los relés de sobrecorriente, aunque no se realiza un análisis sobre la aplicación en la práctica de tener relés de sobrecorriente con diferentes tipos de curvas, ni el efecto en la coordinación de las protecciones de sobrecorriente de fases con las protecciones de sobrecorriente de tierra. En [61] se propone un método de coordinación de relés basado ABC. Este simula el comportamiento inteligente de las colonias de abejas mieleras. En el ABC, la colonia artificial contiene tres grupos de abejas: abejas empleadas y abejas desempleadas, observadoras y exploradoras las cuales distribuyen sus funciones para explorar el espacio de solución.

En [60] se propone una nueva aproximación para la coordinación óptima de relés de sobrecorriente basado en el algoritmo PSO, en este trabajo se tiene en cuenta en el proceso de optimización el TDS y el PMS, donde un algoritmo PSO existente es mejorado mediante el empleo de una nueva función objetivo.

La metodología propuesta por [56] es un método híbrido que toma encuentra el TDS como un valor continuo y la corriente de arranque como un parámetro discreto que es considerado en el procedimiento de optimización. Para este método se consideran tanto las fallas cercanas como las fallas lejanas en las restricciones del problema de coordinación óptima, donde antes de resolver el problema se determinan los pares de relés principal y de respaldo.

En la referencia [9] se propone también un método híbrido para la determinación de los ajustes de las protecciones de sobrecorriente operando como respaldo, teniendo en cuenta la coordinación con los tiempos de operación de la zona dos de las protecciones distancia. El método híbrido propuesto está dividido en dos partes, lineal y no lineal. Para el desarrollo de la parte no lineal, el PSO es empleado para la obtención de las corrientes de arranque de los relés de sobrecorriente, y después se usa la programación lineal para determinar los valores óptimos de TDS y tiempo de zona dos de los relés en la parte lineal. Los resultados obtenidos por esta metodología fueron iguales a los obtenidos por algoritmos genéticos pero en menor tiempo.

La referencia [57] propone que sabiendo que los relés de sobrecorriente permiten ajustes continuos para los diales de tiempo y ajustes de corriente de arranque discretos, el problema de la coordinación de relés es formulado como un problema de programación entera mixta, donde la corriente de arranque de cada relé es escrita como la sumatoria de cada una de los ajustes de corrientes de arranques disponibles multiplicadas por una variable binaria. Al adicionar las ecuaciones anteriores al problema lineal tradicional se llega al problema de programación no lineal entero mixto. En el algoritmo propuesto, se emplea el método de punto interior para obtener una solución factible inicial. Esto es realizado inicializando las corrientes de arranque aleatoriamente, de esta manera el problema llega a ser lineal y los valores de TDS son calculados usando el método de punto interior. Otra modificación aplicada al PSO original para superar la ocurrencia de algunas partículas no factibles, en vez de actualizar la posición de todas las partículas al mismo tiempo, las partículas son actualizadas una después de la otra. Se actualiza la posición de la partícula en la primera dimensión, y entonces se verifica si después de este cambio, la partícula aún continua dentro del espacio de búsqueda factible, entonces se acepta la actualización, de lo contrario, la partícula mantiene su posición anterior.

7. CONCLUSIONES E

n este trabajo se presenta el estado del arte en las técnicas empleadas para la optimización de la coordinación de relés de sobrecorriente en sistemas eléctricos de potencia. Se describen las consideraciones asociadas a cada uno de los métodos presentados. Algunas de las técnicas empleadas muestran que, mediante el uso de inteligencia artificial es posible obtener óptimos globales a los problemas de coordinación de relés de protecciones.

Las técnicas de optimización han permitido eliminar la necesidad de hallar los puntos de quiebre (BP), la cual es una tarea ardua, empleados por las metodologías convencionales para determinar los lazos de donde se inicia la coordinación de los relés.

Del análisis de las referencias encontradas hasta el año 2014, se observó que la programación lineal y las técnicas metaheurísticas, en especial los algoritmos genéticos, han sido ampliamente empleados como herramienta de solución al problema de la coordinación de los relés de sobrecorriente, especialmente por su facilidad de implementación. Las distintas referencias reportan que con el empleo de técnicas metaheurísticas ha sido posible la obtención de mejores resultados que con otras técnicas de programación matemática clásica.

8. REFERENCIAS BIBLIOGRÁFICAS

[1] Jingjing Zhang, Ming Ding, Summary of research on hidden failures in protection systems. Memorias, International Conference on Electrical Machines and Systems (ICEMS), 2008.

[2] CIGRÉ, Adaptive protections and control – Final report, Working Group 34.02, August 1995.

[3] Mazlumi Kazem, Abyaneh Hossein A., Relay coordination and protection failure effects on reliability indices in an interconnected subtransmission system, Electric Power System Research, 79, 1011–1017, 2009.

[4] Mansour, Mohamed M., Mekhamer, Said F., El– Kharbawe, Nehad El–Serrif. A modified particle swarm optimizer for the coordination of directional overcurrent relays, IEEE transactions on power delivery, 22, 1400–1410, 2007.

[5] Estrada C., Nestor J., Gómez C. Oscar, Coordinación de relés de sobrecorriente usando programación lineal. Revista Energía y Computación., 15, 29–36, 2007.

[6] Yinhong, Li, Dongyuan, Shi, Xianzhong, Duan. An integrated power system relay coordination software. Memorias, Power engineering society summer meeting, Vancouver, Canada, 1315– 1318, Julio, 2001

[7] Madani, S. M.; Rijanto, H., A new approach for designing of power system protection. Documento presentado en Sixth International Conference on Developments in Power System Protection, marzo 1997.

[8] Urdaneta, Alberto J., Nadira, Ramón, Pérez J., Luis G., Optimal coordination of directional overcurrent relays in interconnected power systems, IEEE Transactions on Power Delivery, 3, 903–911,1988.

[9] Abyane Hossien A., Faez Karim, Karegar Hossien K., A new method for overcurrent relay (O/C) using neural network and fuzzy logic, IEEE TENCON, 407–410 1997.

[10] Hussain M.H., Rahim S. R. A., Musirin I., Optimal overcurrent relay coordination: a review, Procedia Engineering MUCET 2012, 53, 332–336, 2013

[11] Abyaneh, Hossein A., Hashemi K., Somayeh S., Razavi, Farzad, Chabanloo M., Reza., A new genetic algorithm method for optimal coordination of overcurrent relays in a mixed protection scheme with distance relays. Documento presentado en 43rd International Universities Power Engineering Conference UPEC 2008, Padova, Italia, septiembre de 2008.

[12] Chabanloo, Reza M., Abyaneh, Hossein A., Hashemi K., Somayeh S., A new genetic algorithm for optimal coordination of overcurrent and distance relays considering various characteristics for overcurrent relays. Documento presentado en 2^nd IEEE International Power and Energy, Johor Bahru, Malaysia, diciembre de 2008.

[13] Kezunovic, M., Intelligent systems in protection engineering. Documento presentado en 2000 International Conference on Power System Technology, Perth, Australia, diciembre de 2000.

[14] Bittencourt, A. A., Carvalho M.R., Adaptive strategies in power system protection using artificial intelligence techniques. Documento presentado en 15th International Conference on Intelligent System Applications to Power Systems. ISAP '09., Curitiba, Brazil, noviembre de 2009.

[15] Birla Dinesh, Maheshwari Rudra P., Gupta Hari O., Time–overcurrent relay coordination: A review, International Journal of Emerginng Electric Power System, 2, 1–13. 2005.

[16] Phadke, A. G., Thorp J.S., Synchronized phasor measurements and their applications. Springer, New York, 2008.

[17] León, Ramón Alberto. Medición Fasorial en el SIN. Documento presentado en Tercera Jornada Técnica de Transmisión, Comité Nacional de Operación – CNO, Bogotá, Colombia, noviembre de 2010.

[18] Hart, David G., Uy, David., Gharpure, Vasudev., Novosel, Damir., Karlsson, Daniel., Kaba, Mehmet., Unidades PMU Supervisión de las redes eléctricas: un nuevo enfoque., revista ABB, 58–61, 2001.

[19] XM – Expertos en Mercados, Taller tecnología e implementación de redes inteligentes en el sector eléctrico colombiano, febrero 2011.

[20] Raza A. Syed, Mahmood Tahir, Ali B. Syed B., Kashif N. M., Application of optimization techniques in overcurrent relay coordination–A review. World applied sciences journal 28, 2, 259–265, 2013.

[21] Madan, S., Bollinger K.E., Applications of intelligence in power systems, Electric Power Systems Research, 41, 117–131, 1997.

[22] Ezzeddine Mazhar, Kaczmarek Robert., A novel method for optimal coordination of directional overcurrent relays considering their available discrete settings and several operation characteristics, Electric Power System Research, 81, 1475–1481, 2011.

[23] Sueiro José A., Diaz–dorado Eloy, Míguez Edilmiro, Cidrás José., Coordination of directional overcurrent relay using evolutionary algorithm and linear programming, Electrical Power and Energy Systems, 42, 299–305, 2012.

[24] Jamali S., Pourtandorost M., New approach to coordination of distance relay zone–2 with overcurrent protection using linear programming methods. Documento presentado en 39th International Universities Power Engineering Conference UPEC 2004, Britol, UK, septiembre de 2004

[25] Abyaneh, H.A., Al–Dabbagh, M., Karegar, H.K., Sadeghi, S.H.H., Khan, R.A.J., A new optimal approach for coordination of overcurrent relays in interconnected power systems, Power Delivery, IEEE Transactions on , 18, 430–435, 2003.

[26] Karegar Hossien K., Abyaneh Hossein A., Ohis Vivian, Meshkin Matin., Pre–processing of optimal coordination of overcurrent relays, Electric Power System Research, 75, 134–141, 2005.

[27] Baran M., El–Markabi I., Adaptive over current protection for distribution feeders with distributed generators. Documento presentado en Power Systems Conference and Exposition 2004, New York, USA, octubre de 2004.

[28] Urdaneta Alberto J., Restrepo Harold., Márquez Saul., Sánchez Jorge, Coordination of directional overcurrent relay timing using linear programming, IEEE Transactions on Power Delivery, 11, 122–129, 1996.

[29] Urdaneta, Alberto J., Pérez, Luis G., Restrepo, Harold., Optimal coordination of directional overcurrent relays considering dynamic changes in the network topology, IEEE Transactions on Power Delivery, 12, 1458– 1464, 1997.

[30] Urdaneta Alberto J., Pérez Luis G., Optimal coordination of directional overcurrent relays considering definite time backup relaying, IEEE Transactions on Power Delivery, 14, 1276– 1284, 1999.

[31] Urdaneta Alberto J., Pérez Luis G., Optimal computation of distance relays second zone timing in a mixed protection scheme with directional overcurrent relays, IEEE Transactions on Power Delivery, 16, 385–388, 2001.

[32] Zapata, Carlos J., Mejía, Germán., Coordinación de relés de sobrecorriente en sistemas radiales utilizando programación lineal, Scientia et Technica, 22, 2003.

[33] Pérez Luis G., Urdaneta Alberto J., Calculation of optimum directional overcurrent relays settings: the parallel case, IEEE Power Engineering Review, 68–69, 2000.

[34] Pérez Luis G., et al., Comparison of time coordination feasibility criteria for a subtransmission protection scheme, IEEE, 314– 319, 1998.

[35] Zapata Carlos J., Mejía Germán E., Coordinación de relés de sobrecorriente en sistemas enmallados utilizando programación lineal, Scientia et Technica año XI, 23, 1–6, 2003 .

[36] Estrada, C., Nestor, J., Gómez, C. Oscar, Garcés R. Alejandro., Coordinación de relés de sobrecorriente usando el método de optimización de puntos interiores, Scientia et Technica, 32, 25–30, 2006.

[37] Urdaneta Alberto J., Pérez Luis G., Restrepo Harold., Sánchez Jorge., Fajardo Juan., Consideration of the transient configurations in the optimal coordination problem of directional overcurrent relays, IEEE, 169–173, 1995.

[38] Zeineldin H., El–Saadany E. F., Salama M. A., A novel problem formulation for directional overcurrent relay coordination. Documento presentado en LESCOPE–04 Large Engineering systems Conference on Power Engineering, 48– 52, Halifax, Canadá, Julio de 2004.

[39] Ralhan, S., Ray, S., Directional overcurrent relays coordination using linear programming intervals: A comparative analysis. Documento presentado en Annual IEEE India Conference (INDICON), Mumbay, India, diciembre 2013.

[40] Chattopadhyay Bijoy, Sachdev M.S., Sidhu T.S., An on–line relay coordination algorithm for adaptive protection using linear programming technique, IEEE Transactions on Power Delivery, 11, 165–173, 1996.

[41] Li K. K., So C. W., Evolutionary algorithm for protection relay setting coordination, Power system technology, 2, 813–817, 2000.

[42] C.W. SO., K.K. LI., Overcurrent relay coordination by evolutionary programming, Electric Power Research, 53, 83–90, 2000.

[43] Moirangthem, Joymala., K. R. Krishnanand., Saranjit, N., Optimal coordination of overcurrent relay using an enhanced discrete differential evolution algorithm in a distribution system with DG. Documento presentado en 2011 Energy, Automation and signal ICEAS, Odisha, India, 2011.

[44] Chelliah Thanga R., Thangaraj Radha, Allamsetty Srikanth, Pant Millie, Coordination of directional overcurrent relays using opposition based chaotic differential evolution algorithm, Electrical Power and Energy Systems 55, 341– 350, 2014.

[45] Moirangthem, J., Krishnanand, K.R., Dash, S.S., Ramaswami, R., Adaptive differential evolution algorithm for solving non–linear coordination problem of directional overcurrent relays, Generation, Transmission & Distribution, IET , 7, 329–336, 2013.

[46] Thangaraj, Radha., Pant, Millie., Deep, Kusum., Optimal coordination of over–current relays using modified differential evolution algorithms, Engineering Applications of Artificial Intelligence, 23, 820–829, 2010.

[47] Bedekar, P.P., Bhide, S.R., Kale, V.S., Optimum coordination of overcurrent relays in distribution system using genetic algorithm. Documento presentado en Third International Conference Power Systems, Kharagpur, India, diciembre de 2009.

[48] Singh, Dharmendra Kumar., Gupta, S., Optimal Coordination of Directional Overcurrent Relays: A Genetic Algorithm Approach. Documento presentado en 2012 IEEE Students' Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 2012.

[49] Bedekar, Prashant P., Bhide Sudhir R., Optimum coordination of overcurrent relay timing using continuous genetic algorithm, Expert Systems with Applications, 38, 11286– 11292, 2011.

[50] Mesa Quintero, Noé A., Metodología para el ajuste óptimo de relés de protección en líneas de transmisión [Ms. Thesis], Medellín, Antiquia: Universidad de Antioquia, 2012.

[51] Kamangar, S.; Abyaneh, H.A.; Chabanloo, R.M.; Razavi, F., A new genetic algorithm method for optimal coordination of overcurrent and earth fault relays in networks with different levels of voltages. Memorias, 2009 IEEE PowerTech. Bucharest, Romania, Junio 2009.

[52] Mohammadi, R., Abyaneh, H.A., Rudsari, H.M., Fathi, S.H., Rastegar, Hasan., Overcurrent Relays Coordination Considering the Priority of Constraints, IEEE Transactions on Power Delivery, 26, 1927–1938, 2011.

[53] Parve, Manjussha K., Comparison of overcurrent relay coordination by using fuzzy and genetic algorithm methods, OSR Journal of Electrical and Electronics Engineering, 5, 21–28, 2013.

[54] Chen, Chao–Rong., Lee, Chen–Hung., Chang, Chi–Juin., Optimal overcurrent relay coordination in power distribution system using a new approach, Electrical Power and Energy Systems, 45, 217–222, 2012.

[55] Sadeh, Javad., Amintojjar, Vahid., Bashir, Mohsen., Coordination of overcurrent and distance relays using hybrid particle swarm optimization. Documento presentado en Conference on International Advanced Power System Automation and Protection (APAP), Beijing, China, 2011.

[56] Bashir, M., Taghizadeh, M., Sadeh, J., Mashhadi, H.R., A New Hybrid Particle Swarm Optimization for Optimal Coordination of Over Current Relay. Documento presentado en International Conference on Power System Technology, Zhejiang–Hangzhou, China, 2010.

[57] Zeineldin, H. H., El–Saadany, E. F., Salama, M.M.A., Optimal coordination of overcurrent relays using a modified particle swarm optimization, Electric Power Systems Research, 76, 988–995, 2006.

[58] Yang, Ming–Ta., Liu An., Applying hybrid PSO to optimize directional overcurrent relay coordination in variable network topologies, Journal of Applied Mathematics, Hindawi Publishing Corporation, 2013, 1–9, 2013.

[59] Bernardes, W.M.S., de P Santos, F.M., Asada, E.N., de Souza, S.A., Ramos, M.J., Discrete metaheuristic for coordination of directional overcurrent relays in meshed systems. Documento presentado en 2013 IEEE PES Conference On Innovative Smart Grid Technologies Latin America (ISGT LA), Sao Paulo, Brazil, abril de 2013.

[60] Asadi, M.R., Kouhsari, S.M., Optimal Overcurrent Relays Coordination using Particle– Swarm–Optimization Algorithm. Documento presentado en Power Systems Conference and Exposition PSCE '09, Seatle, USA, 2009.

[61] Uthitsunthorn, D., Pao–La–Or, P., Kulworawanichpong, T., Optimal overcurrent relay coordination using artificial bees colony algorithm. Documento presentado en 8th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI–CON), Khon Kaen, Thaniland, 2011.

[62] Birla, D.; Maheshwari, R.P.; Gupta, H.O., A new nonlinear directional overcurrent relay coordination technique, and banes and boons of near–end faults based approach, Power Delivery, IEEE Transactions on , 21, 1176– 1182, 2006.

[63] Benabid R, Zellagui M., Chaghi A., Boudour M., Application of Firefly Algorithm for Optimal Directional Overcurrent Relays Coordination in the Presence of IFCL, International Journal of Intelligent Systems and Applications (IJISA), MECS Publisher, 6, 44–53, 2014.

[64] Tueitemwong Kamphol., Premrudeepreechacharn Suttichai., Expert system for protection coordination of distribution system with distributed generators, Electrical Power and Energy Systems, 33, 466–471, 2011.

[65] Mahari, A.; Seyedi, H., An analytic approach for optimal coordination of overcurrent relays, Generation, Transmission & Distribution, IET , 7, 674–680, 2013.

[66] INTERNATIONAL ELECTROTECHNICAL COMMISSION IEC, Measuring relays and protection equipment – Part 151: Functional requirements for over/under current protection, IEC 60255–151 ed1.0, Switzerland, 2008.

[67] Abdelaziz A.Y., Talaat H.E.A., Nosseir, Hajjar Ammar A., An adaptive protection scheme por optimal coordination of overcurrent relays, Electric Power Systems Research, 6, 1–9, 2002.

[68] Souza Jr. F. C., Souza Benemar A., Adaptive overcurrent adjustment settings: a case study using RTDS. Documento presentado en 2013 IEEE PES Conference On Innovative Smart Grid Technologies Latin America (ISGT LA), Sao Paulo, Brazil, abril de 2013.