ARTÍCULOS

MODELADO Y CONTROL DE UN PROTOTIPO DE AERONAVE NO TRIPULADO DE ALA FIJA

MODELING AND CONTROL OF A PROTOTYPE OF UNMANNED AIRCRAFT WITH FIXED WING

Leonardo Enrique Solaque Guzmán ¹

1 Doctor en Ingeniería. Profesor asociado de la Universidad Militar Nueva Granada y adscrito al programa de Ingeniería Mecatrónica. E–mail: leonardo.solaque@unimilitar.edu.co

Recibido: 09 de Diciembre de 2013. Aceptado: 29 de Mayo de 2014.

RESUMEN

El propósito de este trabajo es dar un acercamiento al modelado y control de aviones no tripulados de pequeña envergadura, orientado a hacer una implementación real. Una representación matemática se presenta, mostrando la dificultad del comportamiento aerodinámico. Un control no lineal a partir del desacople del vuelo lateral y longitudinal es presentado. Al final, se muestra resultados en simulación y se propone un trabajo futuro de implementación en un prototipo real, construido en la Universidad Militar Nueva Granada

Palabras clave: UAV, Modelado dinámico, Control, Desacople, Vuelo lateral, Vuelo Longitudinal.

ABSTRACT

The purpose of this work is giving an approach to the modeling and control of small scale UAVs, in order to make a real implementation. A mathematical representation is presented evidencing the difficulty of modeling the aerodynamic behavior. A non–lineal control based on decoupling of lateral and longitudinal flight is presented. In the end of the article, the simulation results are shown and the implementation on a real prototype to be built in the Military University Nueva Granada is proposed as future work.

Key words: UAV, Dynamic modeling, Control, Decoupling, Lateral flight, Longitudinal flight.

1. INTRODUCCIÓN

En el contexto de aviones no tripulados, conocido como UAV por su nombre en ingles Unmanned Aereal Vehicle, la Universidad Militar Nueva Granada – UMNG viene incursionando en el tema, mediante proyectos de investigación, con financiación interna y adscritos al programa de Ingeniería Mecatrónica. En estos, se ha planteado el diseño y construcción de una aeronave de ala fija de pequeña envergadura, tal como se presenta en la Fig. 1.

En la conceptualización, diseño mecánico y construcción de la aeronave, se consideró un prototipo capaz de realizar vuelos con bajo consumo energético, sistema de propulsión eléctrica y carga paga de por lo menos 2kg.

Con esta plataforma, se ha hecho el recorrido de plantear un modelo dinámico y prueba de controles de vuelo a nivel simulación, bajo el concepto de desacople en la fase de vuelo crucero, en vuelo lateral y vuelo longitudinal, con fines futuros de implementación en hardware.

En la literatura, muchas empresas, centros de investigación e instituciones Universitarias vienen adelantando estudios permanentes en estas plataformas. MicroPilot [1] es un ejemplo de la industria, que presenta desarrollos en auto–pilotos, estaciones de control, comunicaciones, integración a nivel Software–Hardware o demostraciones de la integración de servicios para este tipo de aeronaves, entre otros. En un contexto internacional y orientado a la investigación desde instituciones universitarias, el EPFL y su laboratorio de sistemas inteligentes [2], está realizando propuestas novedosas en el campo de los UAV, tal como los Drones capaces de desplazarse y recuperarse, aun si tienen una colisión. La Universidad de Sidney [3], realiza un concurso abierto al público en UAV, además de realizar investigación permanente en el campo, con aportes en la navegación autónoma y formación de robots para tareas cooperativas. De igual manera lo hace el MIT [4], desarrollando aplicaciones en trabajo cooperativo o tareas especificas en misiones.

En un contexto nacional, se encuentran desarrollos aislados. La Universidad Eafit, en cabeza de Carlos Mario Vélez [5], presenta desarrollos en helicópteros autónomos, modelado e identificación paramétrica. La Universidad del Cauca, en cabeza de Jorge Andrés Córdoba [6], desarrolla prototipos de ala fija y controles basados en lógica difusa. Otros exponentes en el contexto nacional son la Universidad Bolivariana de Medellín y la San Buenaventura–sede Bogotá, entre otras.

A nivel de desarrollos o incursión en técnicas de control, identificación o misiones, muchos trabajos pueden ser referenciados. Kerr [7] presenta desarrollos con compensadores y controles saturados. MicroPilot [1], implementa en sus autopilotos, controles tipo PID anidados. Chalmers [8] presenta trabajos cooperativos, donde usan tecnología de MicroPilot para hacer telemetría. El ENAC [9] trabaja en cooperación de robots aéreos y terrestres, cartografía y formación en misiones. Así, el tema está abierto a la optimización y aplicaciones propias, bajo entornos específicos. En [10] se presenta el control de un avión de ala fija con dependencia y no dependencia del GPS, debido a que nacen dificultades cuando sobrevuela en terrenos bajos y con obstáculos, y se genera pérdidas en datos del GPS. [11] realiza diseño de controles propios, mediante la técnica de compensadores de adelanto de fase y PID para controlar altitud. Un controlador PID integrado con Filtro de Kalman Extendido (EKF) para el control de attitude a nivel simulación es mostrado en [12]. En [13] se presenta sintonización por Ziegler–Nichols para el control de attitude y altitud, realizando pruebas usando Hardware in the Loop. [14] Presenta estimación de parámetros para sintonización de los controles de aeronaves de ala fija. [15] presenta técnicas Backstepping y modos deslizantes para la estabilización de un avión de ala fija. La aplicación de un nuevo sistema de control, que consiste en combinar la inversión dinámica no lineal con la asignación de control multivariado basado en spline–simplex, es presentado en [16]. Un esquema de compensación no lineal con antiwindup, es propuesto en [17], donde el sistema de control de ciclo interno consiste en inversión dinámica no lineal, mientras que el control de ciclo externo consiste en un controlador PID.

La UMNG – Programa de Mecatrónica y el Grupo de Investigación en Desarrollos y Aplicaciones Mecatrónicas – GIDAM, realiza esfuerzos encaminados a cerrar un poco esta brecha. En esta dirección, este trabajo pretende acercar a la formulación de leyes de control, orientadas a la implementación sobre prototipos reales.

El presente artículo esta organizado así: la introducción relaciona una plataforma que fue diseñada y construida en la UMNG, y muestra un contexto nacional e internacional de lo que se viene realizando. La sección 2, presenta el modelo dinámico de una aeronave. Una técnica de diseño basada en linealización extendida, para la construcción de las leyes de control, sobre el principio de vuelos estables a baja velocidad (vuelo crucero) – desacople de la dinámica lateral y longitudinal, se encuentran en la sección 3. Algunos resultados de simulación son mostrados en la sección 4 y por último, se abordan algunas conclusiones.

2. METODOLOGIA

2.1 MODELO DINAMICO DEL SISTEMA

Antes de iniciar a conceptualizar y diseñar las leyes de control, se requiere de un estudio adecuado de la dinámica del sistema. Para esto, se considera las ecuaciones de movimiento de un cuerpo rígido en el plano 3D. Para complementar el anterior modelo, se considera el comportamiento aerodinámico del sistema, y para la determinación de los coeficientes aerodinámicos, se considera software de fluidos dinámicos – CFD, sintetizados en aportes que se reflejan en ecuaciones relativamente simples para el presente artículo.

2.1.1 Cinemática

Para describir la dinámica de un UAV en 3D, es necesario considerar los sistemas referenciales tierra R_o , cuerpo R_b y aerodinámico R_a. La matriz de cosenos directores que da el paso entre el sistema R_o y R_b es la presentada en Ec. 1.

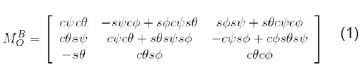
Donde s = sin y c = cos. Esta resulta de realizar rotaciones sobre los ejes, normalmente conocidos como los ángulos de Euler. La matriz para ir de R_b a R_a está dada por la Ec. 2.

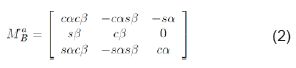
Los sistemas coordenados referenciales antes mencionados, son ilustrados en la Fig. 2.

Los siguientes son supuestos para la obtención del modelo:

1. El sistema es considerado un cuerpo rígido y simétrico en el plano XZ del sistema R_b .
2. El sistema se considera de masa constante
3. El movimiento del sistema es constante con respecto a la distancia donde efectuará los vuelos (no se afecta por los movimientos de la tierra).
4. Se considera el viento medido desde tierra como perturbación.

2.1.2 Ecuaciones de movimiento

Mediante la teoría de momento lineal, momento rotacional y energía cinética, es posible obtener la ecuación de movimiento traslacional y rotacional del sistema, tal como se presenta en Ec. 3.

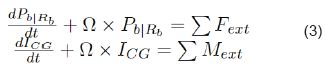
Para un vector descrito en Rb , rotando a una velocidad Ω, se tiene que el cambio en la cantidad de movimiento es 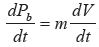, siendo V = u_i + v _j + w_k , m la matriz de masas, Ω = p_i + q _j + r_k e I_CG = I_xi + I_yj + I_zk +(términos acoplados en el plano I_xy ). La Ec. 3. puede ser reescrita como

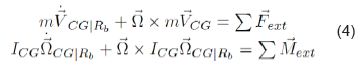
Donde los productos cruz del lado izquierdo de Ec. 4 se asocian a fuerzas centrifugas y de coriolis. Finalmente, la ecuación dinámica del aeromodelo puede ser formulada por

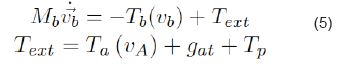
Donde T_ext está formado por los aportes de los fenómenos aerodinámicos T_a (v_a ), fenómenos asociados a la fuerza de gravedad g_at , y la fuerza que porta el sistema propulsor T_p . La matriz M_b se presenta en la Ec. 6 y el término T_b en Ec. 7.

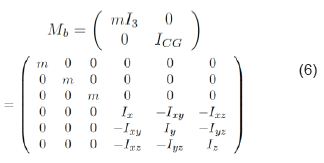
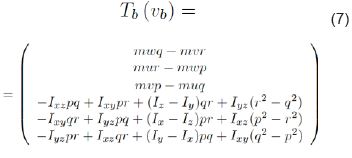
2.1.3 Fenómenos gravitacionales

La fuerza del peso, es conveniente considerarla siempre sobre el eje z del sistema coordenado R_o , y realizar la translación al sistema R_b, donde se hace la sumatoria de fuerzas. Al aplicar la matriz de rotación 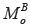, se tiene la expresión de la Ec. 8.

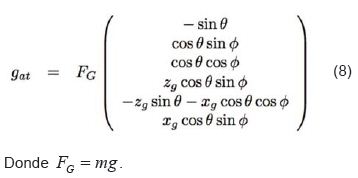
2.1.4 Fenómenos propiciados por el empuje

Dependiendo de la ubicación del propulsor en la estructura, se pueden tener ángulos asociados al vector de fuerza del elemento propulsor. Para el caso de la estructura de la Fig. 1, el motor está alojado paralelo al eje x del sistema Rb. Si existe un ángulo de desvío entre el eje X y el vector de fuerza (tomado como μ ), este debe ser considerado, así como la ubicación de este motor cuando este no está en el centro de gravedad (ver [18]). El vector de fuerzas queda expresado como en Ec. 9.

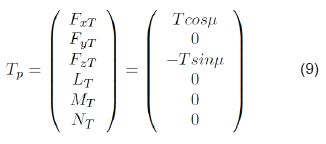
2.1.5 Efectos aerodinámicos.

Para la descripción de los efectos aerodinámicos que actúan sobre el avión, se debe considerar la teoría de un cuerpo cualquiera en movimiento dentro de un fluido. Para disminuir la complejidad de las ecuaciones, se hace el supuesto que el aeromodelo se desplazará a velocidades bajas (por debajo de los 100k /h), lo que conduce a un número de mach pequeño, haciendo posible considerar la masa volumétrica constante ( P_∞ = P ). El avión no supera los 200m de altitud. Lo anterior conduce a la ecuación de aporte aerodinámico descrita en Ec. 10.

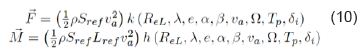
Donde se observa que el fenómeno aerodinámico es dependiente del número de Reynolds, superficies de contacto de la plataforma, ángulo de ataque α , ángulo de deslizamiento β, empuje y deflexión de alerones, entre otros. Este aporte es de los más difíciles de describir matemáticamente, obligando a ir a pruebas iterativas en CFD, o túneles de viento. El objetivo del artículo es hacer una descripción de esta fuerza y no profundizar en ella. Lo anterior conduce a plantear matemáticamente el aporte aerodinámico, como está en la Ec. 11.

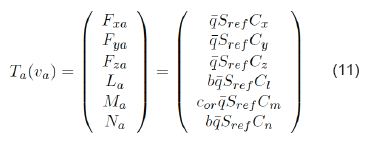
Finalmente, el modelo de simulación es planteado con estas ecuaciones y codificado en Matlab. El diagrama de bloques es presentado en la Fig.3.

2.2 CONTROL BAJO DESACOPLE DINÁMICO

Bajo el supuesto de volar a bajas velocidades y tener dinámicas desacopladas, tal como se da cuando se garantizan puntos de operación donde dejan de ser relevantes otras dinámicas, se tiene desacople en vuelo longitudinal y lateral. En la teoría de control, se consideran este tipo de sistemas como modelos afines [19]. Esto es plantear modelos en los puntos de equilibrio, o puntos de operación cercanos a estos. Lo anterior, permite conceptualizar un modelo para la dinámica longitudinal, presentado en la Ec. 12, y otro para la dinámica lateral, presentada por Ec. 13.

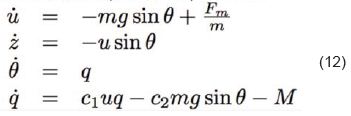
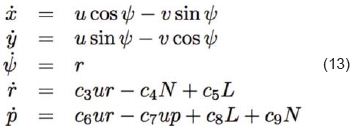
Cabe resaltar que los ángulos de ataque α y deslizamiento β, y la velocidad aerodinámica v_a = V , son consideradas como se presenta en Ec. 14.

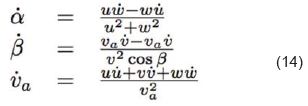
Las ecuaciones anteriores son los modelos usados para plantear la ley de control. Estos reguladores pueden estar enmarcados en el contexto de los sistemas aumentados para estabilidad (Stability Augmentation Systems – SAS [20,21]) y en los sistemas aumentados de control (Control Augmentation Systems – CAS [20,21]). Lo anterior es conducente a considerar los controles como se ilustran por los diagramas de bloques presentados en Fig.4 – Control sobre dinámica longitudinal, y Fig. 5 – Control sobre dinámica lateral.

Tomando como partida la teoría de control no lineal, basada en linealización extendida, siendo un sistema no lineal cualquiera, descrito por 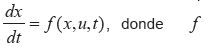es considerado un campo vectorial parametrizado por la entrada u y sobre una variedad de estado M, que puede ser asociado a una hipersuperficie. Así, para cada par 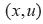, el campo asocia una dirección 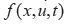tangente a la variedad de estado M en el punto P de coordenada x. Para el caso del UAV, ƒ es un campo de fuerzas y es modificado por la entrada al sistema que son la propulsión y superficies móviles. Al considerar la linealización de primer orden para el sistema, se puede encontrar el modelo en variaciones que se presenta en la Ec. 15.

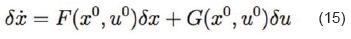
A partir del modelo de la Ec 15, se plantea la ley de control dependiente del punto de operación, tal como lo presenta la Ec. 16.

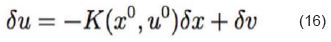
Al realizar la expansión en todo el espacio de trabajo, se debe resolver la integral parcial para la ley de control de la Ec. 16, quedando la ley de control como se muestra en la Ec. 17.

El anterior procedimiento es usado para la determinación de los controles de las variables de estado: velocidad aerodinámica ( v_a), altitud ( z) y dirección (ψ).

3. RESULTADOS EN SIMULACIÓN

Se tiene que luego del diseño del control para el vuelo longitudinal y su respectiva implementación y validación en simulación (esquema Fig.4), se consigue los resultados presentados en las graficas Fig. 6, y Fig. 7.

La Fig. 6, muestra un ligero sobrepaso en la altitud, una vez el sistema se acerca a la referencia. Esto se debe a la dinámica propia del sistema que lo propicia, así se actúe sobre los alerones de elevación.

La Fig. 7 permite evidenciar la anterior afirmación, donde adicional a la señal de control (alerones elevadores), se presenta la variable de estado pitch – θ . La acción de los alerones de elevación se enmarcan en un actuar de 5 segundos para lograr la estabilización del avión en cambios de altitud próximos al punto de operación.

Los resultados del control lateral (esquema Fig. 5) son presentados en las figuras Fig. 8 y Fig. 9. La Fig. 8 relaciona la respuesta del sistema en dirección (heading – ψ ). Se observa que el control es conservador, haciendo llegar el sistema lentamente a su referencia, no importando gastar casi 20 segundos en la maniobra.

La Fig. 9 presenta la acción de los alerones timón (rudder), quienes tienen una acción fuerte al inicio de un cambio, pero lento al realizar la aproximación al objetivo referencia. La variable velocidad en alabeo (r), presenta una estabilización un poco más rápida, viendo que es afectada por las acciones de control, cuando se ejerce sobre la aeronave la deflexión de los alerones cuando se requiere hacer giros.

4. ANÁLISIS DE RESULTADOS

Como se presentó en el ítem anterior, los controles propuestos manifiestan de manera general tener un apropiado comportamiento, aun cuando se diseñaron sobre la base de modelos reducidos.

Cabe resaltar que solo estos resultados son válidos, si se mantienen desplazamientos a baja velocidad y no se entra en las no linealidades fuertes del modelo, donde cobrarían importancia y las leyes de control tendrían que hacer grandes esfuerzos para mantener el UAV controlado, incluso, poder sacarlo a regiones de inestabilidad. Cabe resaltar que aunque no se consideran los acoples entre las dinámicas en los diseños de los controles, estos afrontan adecuadamente la regulación del sistema y mantienen las referencias.

5. CONCLUSIONES

Se contextualizó un modelo para la dinámica de vuelo de un aeromodelo de ala fija. En este, un análisis del comportamiento aerodinámico permitió reducir el modelo, contemplando aportes directos de la deflexión de los alerones. A partir de estos, se planteó un modelo soporte para los diseños de los controles.

A nivel del diseño de los controles, la teoría de linealización extendida – no lineal, mostró buenos resultados, evidenciando la validez de los modelos linealizados en las dinámicas lateral y longitudinal. A nivel de simulación, se observa que los controles presentan acoples que son difíciles de tratar directamente con la teoría de control presentada. Desde aquí, un trabajo futuro puede ser propuesto, mediante la teoría de desacople.

Como conclusión global del desarrollo aquí presentado, se orienta a implementar de manera relativamente fácil sobre sistemas de procesado embarcado, las leyes de control aquí formuladas. Por lo tanto, un trabajo seguido a lo que se expone en el presente documento, se centra en la implementación de los resultados sobre la plataforma aérea real. Cabe resaltar que esta fase de trabajo se está adelantando actualmente. La logística y preparación de esta experimentación no es inmediata y debe ser considerada con todas las variables posibles conducentes a error, de manera que no se arriesgue la estructura.

6. AGRADECIMIENTOS

Se hace reconocimiento a Colciencias por su financiación al proyecto 'Diseño y construcción de un robot tipo vehículo aéreo no tripulado, UAV, con asistencia en vuelo para el monitoreo de redes de transporte eléctrico e hidrocarburos'. Proyecto beneficiado de plan contingencia con código 1123– 521–28738. Igualmente a la Universidad Militar Nueva Granada – UMNG por propiciar los espacios y tiempo de dedicación al proyecto.

7. REFERENCIAS BIBLIOGRÁFICAS

[1] MicroPilot. Disponible en: http://www.micropilot.com/products–horizonmp.htm. Disponible en: http://www.cdc.noaa.gov [consultado el 10 de enero de 2013].

[2] École Polytechnique Fédérale de Lausanner – EPFL – Laboratorio de sistemas inteligentes. Disponible en: http://lis.epfl.ch/ [consultado el 10 de enero de 2013].

[3] Universidad de Sydney – Investigación en UAV & Robotic Aircraf. Disponible en: http://web.aeromech.usyd.edu.au/wwwdocs/uav.ht ml [consultado el 10 de enero de 2013].

[4] Massachusetts Institute of Technology – UAV team. Disponible en: http://web.mit.edu/uav/www/html/about.html [consultado el 10 de enero de 2013].

[5] Presentación de Control de sistemas no tripulados UAS – Carlos Mario Velez. Disponible en: http://www.eafit.edu.co/minisitios/cienciaaplicada/D ocuments/Control%20de%20sistemas%20de%20a eronaves%20no%20tripuladas.pdf [consultado el 10 de enero de 2013].

[6] Notas de EL EFIGENIA EJ–1B MOZART. Disponible en: http://www.compelect.com.co/wpcontent/ plugins/downloadmonitor/ download.php?id=70 [consultado el 10 de enero de 2013].

[7] Kerr, M. ; Postlethwaite, I. ; Sofrony, J., Flight testing of low–order anti–windup compensators for improved handling and PIO suppression'', Proceedings Of The American Control Conference, ISSN: 0743–1619. v.1 fasc.1 p.1776 – 1781, 2008

[8] Chalmers, R., Scheidt D. Et all, Cooperating Unmanned Vehicles. AIAA 1st Intelligent System Technical Conference 20–22 September 2014.

[9] ENAC – Proyecto Paparazzi. Disponible en: https://wiki.paparazziuav.org/wiki/ENAC_UAV_Labo ratory [consultado el 10 de enero de 2013].

[10] M. Garcia, T. Muskardin, A. Viguria, M. Laiacker, A. Ollero, K. Kondak – Analysis and development of a reliable fixed wing UAV control system for mission profiles with restricted GPS availability. 2013 International Conference on Unmanned Aircraft Systems (ICUAS). May 28–31, 2013, Grand Hyatt Atlanta, Atlanta, GA.

[11] Ahsan, M. ; Shafique, K. ; Bin Mansoor, A. ; Mushtaq, M.– Performance comparison of two altitude–control algorithms for a fixed–wing UAV. Computer,Control & Communication (IC4), 2013 3rd International Conference on .25–26 Sept. 2013.

[12] Faizan. A. Warsi, D.Hazry, S. Faiz Ahmed, M. Kamran Joyo, M. Hassan Tanveer, H. Kamarudin, Zuradzman M. Razlan – Yaw, Pitch and Roll Controller Design for Fixed–wing UAV under uncertainty and perturbed Condition. 2014 IEEE 10th International Colloquium on Signal Processing & its Applications (CSPA2014), 7 – 9 Mac. 2014, Kuala Lumpur, Malaysia.

[13] Sufendi, Bambang Riyanto Trilaksono, Syahron Hasbi Nasution and Eko Budi Purwanto – Design and implementation of hardware–in–the–loopsimulation for uav using pid control method. 2013 3rd International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering (ICICI–BME). Bandung, November 7–8, 2013.

[14] Li Meng, Liu Li, S.M. Veres – Aerodynamic Parameter Estimation of an Unmanned Aerial Vehicle Based on Extended Kalman Filter and Its Higher Order Approach. Advanced Computer Control (ICACC), 2010 2nd International Conference on, Publication Year: 2010 , Page(s): 526 – 531.

[15] Qinglei Hu, Bo Li, and Youmin Zhang. ''Nonlinear Proportional–Derivative Control Incorporating Closed–Loop Control Allocation for Spacecraft'', Journal of Guidance, Control, and Dynamics, Vol. 37, No. 3 (2014), pp. 799–812. doi: 10.2514/1.61815.

[16] H. J. Tol, C. C. de Visser, E. van Kampen, and Q. P. Chu. ''Nonlinear Multivariate Spline–Based Control Allocation for High–Performance Aircraft''. doi: 10.2514/1.G000065.

[17] Prathyush P. Menon, Mark Lowenberg, Guido Herrmann, Matthew C. Turner, Declan G. Bates, and Ian Postlethwaite. ''Experimental Implementation of a Nonlinear Dynamic Inversion Controller with Antiwindup'', Journal of Guidance, Control, and Dynamics, Vol. 36, No. 4 (2013), pp. 1035–1046. doi: 10.2514/1.59027.

[18] Solaque, L. Modelado y control de dirigibles. [PhD Thesis]. Toulouse, FR: Instituto Nacional de Ciencias Aplicadas, 2007.

[19] A. J. Fossard. Systèmes non linéaires. Masson, 1993.

[20] J. Blakelock. Automatic control of Aircraft and Missiles, 1991.

[21] B. Stevens and F. Lewis. Aircraft control and simulation, 1992.