ANÁLISIS COMPARATIVO EN LA RESPUESTA LINEAL DE SISTEMAS ESTRUCTURALES MURO-PÓRTICO REPRESENTATIVOS DE BUCARAMANGA INCORPORANDO INTERACCIÓN SUELO ESTRUCTURA

María Alejandra Oliveros Caicedo ¹; David Sebastián Cotes Prieto²; Luis Eduardo Zapata Orduz³;

RESUMEN

El presente artículo evalúo la influencia de la Interacción Suelo – Estructura (ISE) en la respuesta estructural lineal de sistemas muro-pórtico regulares representativos de Bucaramanga-Colombia utilizando el enfoque de subestructura propuesto por Winkler. Se recopiló información de sistemas locales existentes utilizando base de datos oficiales. Mediante el diseño de experimentos factorial 2², se crearon nueve edificios artificiales con diferentes tipos de suelo y número de pisos. Estos edificios fueron diseñados y detallados bajo la idealización de base fija, siguiendo la normativa sismorresistente local. Se llevaron a cabo análisis incluyendo y excluyendo la ISE. Los resultados revelaron que la ISE tuvo influencia significativa en la respuesta lineal de las estructuras ubicadas en zonas de amenaza sísmica alta, presentando variación en el periodo fundamental, cambio en la respuesta modal, incremento de derivas y disminución en el cortante de base. Además, se encontró que también afecta el método de análisis utilizado para el diseño.

Palabras claves: Sistemas representativos; Sistemas muro-pórtico; Interacción suelo-estructura; Análisis lineales; Respuesta estructural.

Recibido: 12 de abril de 2023.Aceptado: 19 de Junio de 2023

Received: April 12, 2023.Accepted: June 19, 2023

STRUCTURAL RESPONSE INCORPORATING SOIL-STRUCTURE INTERACTION IN BUILDINGS WITH WALL-FRAMES SYSTEM REPRESENTATIVE OF BUCARAMANGA

ABSTRACT

This paper evaluates the influence of Soil-Structure Interaction (SSI) on the linear structural response of regular wall-frame systems representative of Bucaramanga-Colombia using the substructure approach proposed by Winkler. Information was collected from existing local systems study using official databases. Using the 22 factorial design of experiments, nine artificial buildings were created with different soil types and number of floors. These buildings were designed and detailed under the fixed base idealization, following the local seismic-resistant regulations. Analyses were carried out including and excluding the ISE. The results revealed that the ISE had a significant influence on the linear response of structures located a high seismic hazard zone, presenting variation in the fundamental period, change in the modal response, increase in drifts and decrease in the base shear. In addition, it was found that it also affects the analysis method for the design.

Keywrods: Representative systems; Wall-frame systems; Soil-structure interaction; Linear Analysis; Structural response.

Cómo citar este artículo: M. Oliveros, D. Cotes, L. Zapata. “Análisis comparativo en la respuesta lineal de sistemas estructurales muro-pórtico representativos de Bucaramanga incorporando Interacción Suelo Estructura”, Revista Politécnica, vol.19, no.38 pp.173-191, 2023. DOI:10.33571/rpolitec.v19n38a11

1. INTRODUCCIÓN

---

El diseño sismo-resistente actual busca dimensionar edificaciones seguras y funcionales con base en hipótesis conservadoras sobre el comportamiento estructural. Una suposición comúnmente utilizada es la de base fija, donde el edificio se asume como perfectamente empotrado en su base, que implica despreciar la rigidez del suelo de cimentación. No obstante, un abordaje para el refinamiento del diseño utilizando las herramientas computacionales es el denominado Interacción Suelo-Estructura (ISE), el cual considera al suelo como un medio deformable y con rigidez finita, tal como se indican en [1-2]. Esta permite captar los efectos de la flexibilidad del suelo sobre la respuesta dinámica y el comportamiento sísmico de la edificación a través de diferentes métodos analíticos como los estudiados por [3–4].

La ciudad de Bucaramanga-Colombia está ubicada en una zona de alta sismicidad, lo que hace preciso evaluar los efectos de la ISE en la respuesta sísmica de sus edificaciones. El Reglamento Colombiano de Construcción Sismo Resistente (NSR-10) [5], establece en su Artículo A.3.4.2.2 (e) la obligación de considerar la ISE en estructuras localizadas en perfiles de suelo de poca rigidez, catalogados como D, E o F. A pesar de esto, la implementación de la ISE en el diseño de estructuras se omite en la práctica por considerarse poco conservadora. Esto se debe a lo descrito por el Artículo A.7.1.2 (NSR-10) [5] y a las contribuciones de otros autores [6-7]. Al incorporar la ISE en el análisis, se esperan periodos más largos debido a la interacción cinemática, tal como se encontró en estudios [8–9], lo que a su vez reduce las fuerzas sísmicas que actúan en la edificación en comparación al modelo de base fija. Pero estos no son los únicos efectos por considerar, estudios ya han demostrado que esta conclusión es errónea desde ejemplos numéricos rigurosos [2] [10] [11] al tener en cuenta los efectos de la interacción inercial. La interacción inercial debido a las influencias adicionales de traslación y rotación puede aumentar las demandas de desplazamiento en el sistema de cimentación-estructura y afectar elementos estructurales como se menciona en [12–13].

Por ejemplo, los sistemas estructurales muro-pórtico proporcionan resistencia y rigidez lateral mayor a un sistema de sólo pórticos, por lo cual, son una excelente alternativa para resistir fuerzas sísmicas en edificaciones de mediana y gran altura, según los resultados en [14]. Sin embargo, se ha demostrado [15] que los efectos de la ISE en edificios de esta tipología, cimentados sobre suelos flexibles, no solo va a presentarse aumento del periodo afectando las aceleraciones utilizadas en el diseño, sino también, balanceo de los muros de corte. Este último genera aumento de demandas en las vigas que conectan los muros de corte, lo que puede resultar en daños inesperados sobre el pórtico por los grandes desplazamientos [16]. Por lo tanto, es necesario evaluar los diferentes impactos que la ISE puede tener en el comportamiento y respuesta estructural del sistema muro-pórtico localizados en sitios de alta sismicidad.

Para modelar la ISE, el estudio [17] destaca el uso común de dos enfoques. El enfoque directo, que representa el suelo-estructura como un medio continuo, pero sus cálculos son computacionalmente costosos y llevan mucho tiempo, y el enfoque simplificado subestructura también conocido como el método de Winkler, donde se representa la flexibilidad del suelo con resortes. Este segundo enfoque ha sido ampliamente utilizado y preferido en la práctica debido a su facilidad de uso y requisitos informáticos mínimos [18-19].

Para modelar la ISE, el estudio [17] destaca el uso común de dos enfoques. El enfoque directo, que representa el suelo-estructura como un medio continuo, pero sus cálculos son computacionalmente costosos y llevan mucho tiempo, y el enfoque simplificado subestructura también conocido como el método de Winkler, donde se representa la flexibilidad del suelo con resortes. Este segundo enfoque ha sido ampliamente utilizado y preferido en la práctica debido a su facilidad de uso y requisitos informáticos mínimos [18-19].

Con base en lo anteriormente mencionado, esta investigación evaluó la influencia de la ISE en sistemas estructurales muro-pórtico regulares representativos de Bucaramanga, utilizando el enfoque simplificado de subestructura propuesto por Winkler [20]. Los edificios estudiados fueron artificiales y su geometría se basó en información obtenida a partir del mapeo de estructuras de este tipo en la ciudad en la base de datos del Departamento Administrativo Nacional de Estadística (DANE) [21] y planeación municipal del Área Metropolitana de Bucaramanga (AMB) [22]. Además, se utilizaron registros de velocidades de onda de corte para estimar la rigidez del suelo obtenidos de la base de datos del Servicio Geológico Colombiano [23]. En total se analizaron 9 edificios artificiales, obtenidos del diseño de experimentos factorial 22, con el objetivo de evaluar los efectos principales e interacciones entre los factores de tipo de suelo y el número de pisos. Finalmente, se compararon las respuestas estructurales de diseño de desplazamientos laterales, periodo fundamental, aceleraciones espectrales, cortante basal y participación de masa entre los modelos con y sin ISE.

2. MATERIALES Y MÉTODO

---

2.1 Sistemas estructurales representativos

Con el objetivo de investigar la influencia del número de pisos y tipos de suelo de fundación en la respuesta estructural de sistemas muro-pórtico localizados en amenaza sísmica alta integrando la ISE, se construyeron modelos artificiales utilizando el diseño de experimentos factorial 2² desde puntos axiales y con punto al centro. Este es un tipo de diseño experimental útil para evaluar efectos principales e interacciones entre factores, en el cual se investigan simultáneamente dos factores y cada factor tiene cuatro niveles diferentes [24]. Para establecer los niveles de números de pisos, se consideraron diversas fuentes de información oficiales. La base de datos del Departamento Administrativo Nacional de Estadística (DANE) [21] y oficinas de planeación municipal de Bucaramanga [22], fueron utilizadas para identificar las características comunes de los sistemas estructurales muro-pórtico existentes en el Área Metropolitana de Bucaramanga (AMB).

Desde la base de datos del DANE [21], se evidenció que los edificios existentes en el AMB predominan entre los 5 y 20 pisos (Figura 1 (a)). De los cuales según oficinas de planeación municipal de Bucaramanga [22] se identificó en la revisión de 10 sistemas estructurales construidos en la última década, que el área más común de sistemas constructivos con muro estructural oscila entre 431.00 m² y 588.23 m². Esta situación se presenta en mayor proporción en edificios entre diez y veinte pisos, como se muestra en la Figura 1(b).

Considerando estos antecedentes y los resultados del estudio realizado por Li Shan [14], donde se evalúa la influencia de la altura en la robustes de edificios de concreto. Se determinó que los niveles para el diseño de experimentos de la variable número de pisos, teniendo en cuenta que tendrían una configuración en planta similar con solicitación de muros estructurales y cimientos superficiales, un nivel inferior de 10 pisos y un nivel superior de 20 pisos.

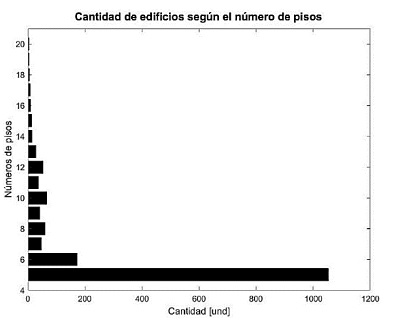
a)

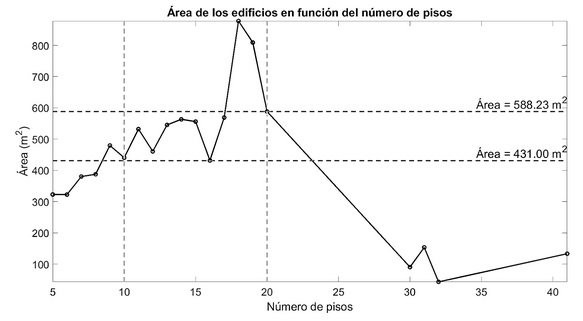
b)

Figura 1 Representación de los edificios ubicados en Bucaramanga y la cantidad de estos [21] [22]

Para definir los niveles del segundo factor del diseño de experimentos (tipo de suelo de fundación), se utilizó la información abierta del Servicio Geológico Colombiano (SGC), específicamente el mapa de velocidad de onda de corte en los primeros 30 metros de profundidad (Vs) [23]. Este parámetro es ampliamente utilizado en la clasificación de perfiles de suelo para el diseño sismorresistente, según normativas como la NSR-10 [5]. Al superponer esta información con la capa de Shapefile correspondiente al casco urbano del AMB en ArcGIS [25], se identificaron diferentes clasificaciones de perfiles de suelos pertenecientes al AMB, desde aquellos con rigidez media (Perfil B) hasta depósitos de suelo de poca rigidez (Perfil D), con valores de Vs que oscilan entre 249.66 m/s y 939.36 m/s (Figura 2).

Es importante destacar que los depósitos de suelo con poca rigidez tienen una gran influencia en la respuesta estructural de los edificios, por lo que su identificación y caracterización en el AMB resulta esencial para el diseño sismorresistente.

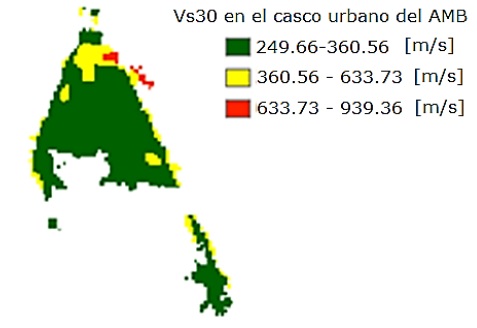
Figura 2 Velocidad de onda de corte de Bucaramanga [23]

A continuación, se utilizó la formulación empírica de la Agencia Federal para el Manejo de Emergencias FEMA P-2091 [16], con el fin de evaluar la importancia de los efectos inerciales de la ISE en los perfiles de suelo B, C y D en edificios de entre 10 y 20 pisos. Esta formulación permite calcular un índice que relaciona la Vs, el periodo fundamental (T) y la altura efectiva del sistema estructural (h’). En donde, valores superiores a 0.10 de este índice indican la presencia de efectos inerciales significativos que no deben ignorarse. En este orden, se encontró que los efectos de la ISE en suelos de rigidez media (Vs>400 m/s) , característica del tipo de perfil de suelo B, no tienen incidencia representativa sobre la respuesta estructural de las edificaciones consideradas. Por lo tanto, la tipología de perfil de suelo B fueron excluidos del estudio de esta investigación.

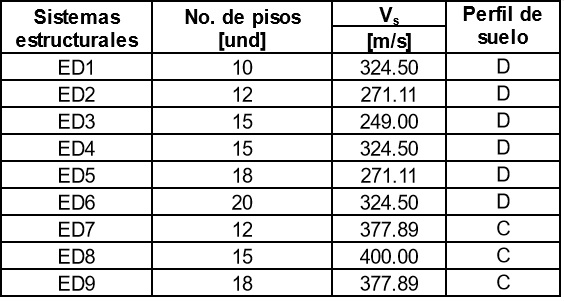
En consecuencia, se asignaron en los niveles del diseño de experimento 2² valores extremos para número de pisos entre [10 – 20] und y velocidad de cortante Vs [249.66 – 400] m/s, lo que permitió obtener las diferentes configuraciones de modelos artificiales para el análisis lineal incorporando la flexibilidad del suelo (con ISE) y asumiendo base fija (sin ISE). Los modelos utilizados para el análisis lineal fueron obtenidos en Minitab® [26] y se encuentran detallados en la Tabla 1. Estos modelos fueron nombrados edificios ED1 – ED9 para facilitar su identificación en función el número de pisos y la Vs.

Tabla 1 Modelos de análisis obtenidos en el diseño de experimentos 2² [26]

2.2 Características tipo en los sistemas estructurales

La configuración geométrica y distribución de los elementos, como viga, columnas y muros, fueron asignadas teniendo en cuenta la revisión de los planos en Planeación Municipal [22]. Estos detalles se presentan de manera resumida en las Tabla 2(a), (b) y

Tabla 3. El objetivo fue obtener una configuración que cumpliera para todos los sistemas estructurales (ED1 – ED9) mencionados en la Tabla 1, el periodo fundamental máximo, solicitación de cimentación superficial, la regularidad en altura y planta, así como la necesidad de muros estructurales para controlar la deriva. Luego de tener en cuenta estas consideraciones, se llegó a la configuración mostrada en la Figura 3.

Tabla 2 [22] (a) Caracterización geométrica de planta estructural de edificaciones en muros ubicadas en Bucaramanga a través de planeación municipal.

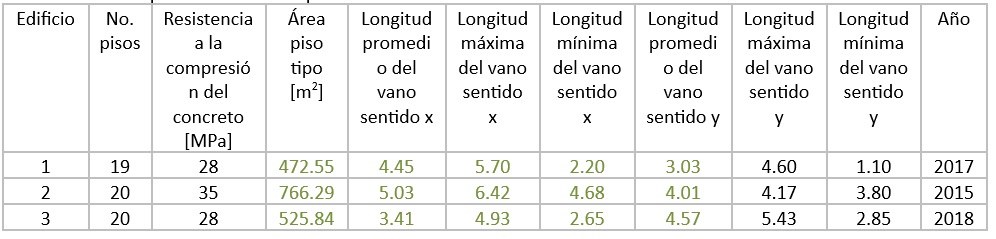
Tabla 2 [22] (b) Caracterización estructural de elementos que conforman la planta estructural de edificaciones con muros ubicadas en Bucaramanga a través de planeación municipal.

Tabla 3 Caracterización estructural de edificaciones en muros ubicadas en Bucaramanga [22]

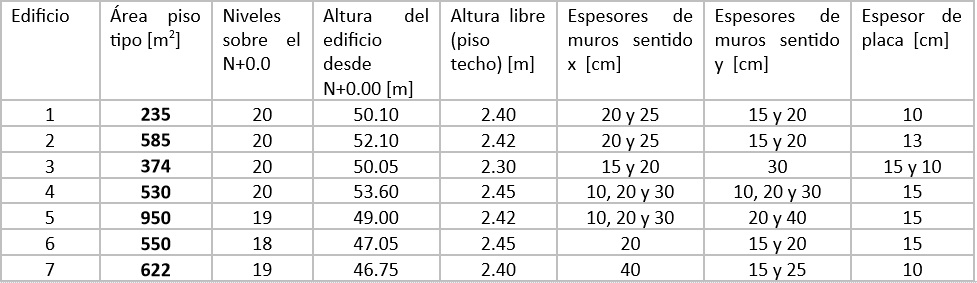
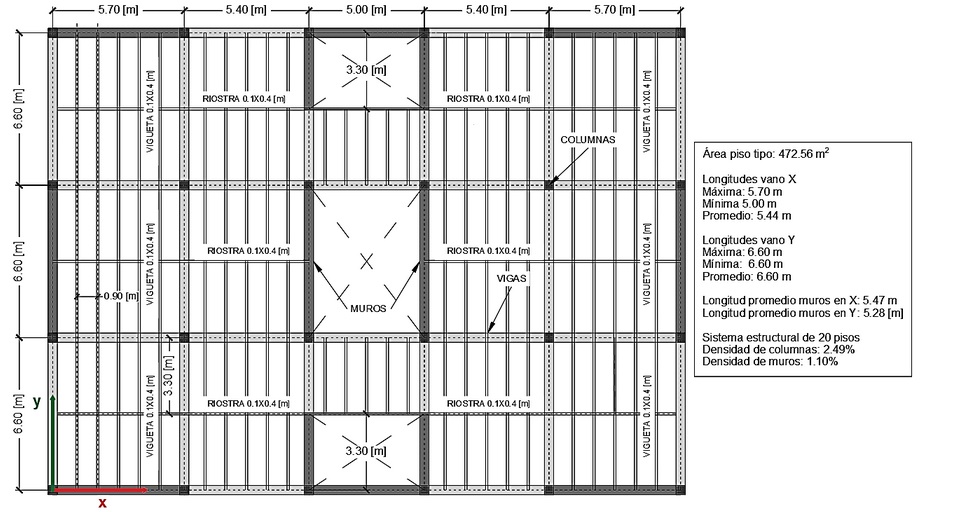
Figura 3 Planta tipo de los sistemas estructurales del modelado

Así mismo, Los modelos (ED1 – ED9) se ubicaron en la ciudad de Bucaramanga, Santander, Colombia; corresponden a un grupo de uso de ocupación normal (Grupo I) y cuentan con una capacidad especial de disipación de energía (DES). El tipo de sistema estructural es un sistema muro – pórtico, que consta de muros de concreto DES como sistema de resistencia sísmica para fuerzas horizontales y pórticos de concreto DES como sistema de resistencia para cargas verticales.

El concreto empleado tiene una resistencia a la compresión fc'=28 MPa, módulo de elasticidad E=24870.06 MPa, y peso específico de γ=24 kN/m³ teniendo en cuenta la información de [21] [22] [23] [5]. Por otro lado, el acero de refuerzo utilizado cuenta con esfuerzo de fluencia mínimo fy=420 MPa, esfuerzo de tracción mínimo fu=581 MPa, esfuerzo de fluencia efectivo fye=470 MPa, esfuerzo de tracción mínimo efectivo fue=660 MPa, módulo de elasticidad E=200000 MPa, y peso específico de γ=78 kN/m³ según el estudio [27] del acero en Colombia.

La carga viva de entrepiso (L) se calculó teniendo en cuenta el tipo de uso residencial de la estructura destinando un 10% del promedio de la carga viva entre escaleras (3.00 kN/m²) y espacios comunes (5.00 kN/m²) y un 90% restante para cuartos y corredores (1.80 kN/m²). La carga viva de cubierta (Lr) se definió como una cubierta de acceso limitado al personal de mantenimiento de 1.80 kN/m².

Las cargas muertas superpuestas por los elementos no estructurales fueron las mínimas sugeridas por la NSR-10 en las Tablas B.3.4.1-1 y B.3.4.3-1 [5]. Para el entrepiso se tuvieron en cuenta fachadas y particiones para sistemas residenciales (3.00 kN/m²), el cielo raso de 0.55 kN/m² (canales suspendidas de acero, ductos mecánicos y pañete en yeso) y adicionalmente el afinado de piso y cubierta (1.60 kN/m²). Para la cubierta se asignaron los mismos elementos no estructurales sin incluir las fachadas y particiones. Estas cargas se calcularon siguiendo de manera detallada los lineamientos establecidos en el Titulo B según NSR-10 [5].

En resumen, las cargas aplicadas a las estructuras, excluyendo el peso propio de los elementos, consistieron para los entrepisos en carga muerta de 5.15 kN/m² y viva de 2.03 kN/m². Para la cubierta 2.15 kN/m² de carga muerta y 1.80 kN/m² de carga viva.

2.3 Características tipo de las propiedades mecánicas de los suelos

Durante la revisión bibliográfica, se encontraron correlaciones entre la Vs y las propiedades mecánicas de los diferentes tipos de suelos presentes en la Tabla 1, necesarias para implementar la ISE. Es importante tener en cuenta que en esta investigación se considera que los suelos friccionantes son homogéneos y constantes en cuanto a su composición y características mecánicas a lo largo de la profundidad portante de 1.30 [m].

Para determinar la densidad de cada suelo (ρ), se realizó una interpolación considerando los rangos establecidos por Mohammad [28] para cada Vs. De igual forma, se definió el coeficiente de Poisson (υ) según [29], fijando un coeficiente de 0.35 para suelos tipo D (Vs< 360 ms) y 0.40 para suelos tipo C (Vs ≥ 360 ms).

En el campo de la mecánica de suelos, se han desarrollado diversas ecuaciones que permiten establecer una relación entre el número de golpes del ensayo de penetración estándar SPT (NSPT) y Vs, en esta investigación se utilizarán las propuestas por [30]. En estudios similares a este, se ha utilizado el enfoque propuesto por Imai [31], el cual es considerado el más común en la literatura. Una vez que se conozcan los valores de Vs y se aplique la formulación de Imai, se pueden obtener valores de NSPT que, posteriormente, se correlacionan con el ángulo de fricción (ϕ) utilizando ecuaciones como la propuesta por los autores Peck, Hanson y Thornburn [32], que presenta una alta correlación de 0.97 entre ϕ y NSPT.

El módulo de corte G y el módulo de elasticidad (E) son propiedades mecánicas que caracterizan el cambio de forma que experimenta un material elástico cuando se aplican esfuerzos cortantes y la resistencia de un material a la deformación elástica, respectivamente. Tanto la referencia [31] y lo recomendado en el Capítulo 6 del FEMA P-2091 [6] proporcionan las formulaciones para obtener el módulo E y el módulo de corte promedio del suelo G0 debajo de la cimentación a niveles de deformación pequeñas. La tabla 19.3-2 del Capítulo 19 de la ASCE 7-16 [33] permite obtener de manera aproximada el módulo G al relacionarlo con el valor de G0 y la aceleración pico efectiva SDS2.5 (Aa según NSR-10 [5])

En la Tabla 4 se especifican las propiedades mecánicas de los suelos, las cuales se obtuvieron mediante las formulaciones anteriores. Estas propiedades son esenciales para llevar a cabo la implementación de la ISE en los modelos de base fija.

Tabla 4 Propiedades mecánicas de los perfiles de suelo del modelado [28 – 33].

2.4 Análisis sísmico de base fija

El diseño estructural es un proceso iterativo, para el cual preliminarmente se definen las secciones de los elementos según la solicitación y parámetros normativos. Para el predimensionamiento de los elementos que forman parte de la resistencia sísmica y entrepiso aligerado, se acataron los capítulos de la NSR-10 [5] (C.7, C.8, C.9, C.10 y C.21). Se obtuvo el periodo fundamental de cada una de las edificaciones a partir de las propiedades del sistema de resistencia sísmica anteriormente descritas y el software ETABS® [34] modelado linealmente elástico y que este no excedieran el periodo fundamental recomendado por la NSR-10 [5] en A.4.2.2.

Los modos de vibración mínimos tenidos en cuenta en el análisis, se calcularon aproximándolos a los grados de libertad totales de los diafragmas rígidos de la estructura [35]. Se evaluó que estos modos involucraran una participación de más del 90% de masa en las direcciones traslacionales como lo describe el Artículo A.5.4.2 de la NSR-10 [5]. Los resultados de cada modo se combinaron mediante el método de Combinación Cuadrática Completa (CQC, por sus siglas en inglés) para obtener el cortante de base y derivas. Se tuvieron en cuenta los efectos ortogonales suponiendo la ocurrencia simultánea del 100% de las fuerzas sísmicas en una dirección y el 30% de las fuerzas sísmicas en dirección perpendicular, como se define en el Artículo A.3.6.3 de la NSR-10 [5].

Se utilizó el Método de FHE para calcular las fuerzas sísmicas Fs, y se aseguró de que los sistemas de perfiles de suelo D y C no excedieran el doble del periodo corto (2Tc) de 1.403 s y 1.294 s, respectivamente. Además, después de asignar los diafragmas, se verificó con los requisitos de la NSR-10 [5] que la configuración de la

Figura 3 para los modelos (ED1 – ED9), no presentara irregularidades de planta y altura.

El coeficiente de capacidad de disipación de energía, R, está determinado por varios factores, tales como el sistema de resistencia sísmica, el grado de irregularidad de la edificación, el grado de redundancia y el grado de capacidad de disipación de energía correspondiente. Para esta investigación, el sistema estructural muro-pórtico el valor de R se define como 7.0 según la Tabla A.3-2 de la NSR-10 [5], junto con la ausencia de irregularidades.

A partir de las Fs determinadas por el método FHE también se controlaron los límites de la deriva como porcentaje de altura de piso según la Tabla A.6.4-1 de la NSR-10 [5]. Una vez considerados todos los aspectos mencionados anteriormente, se procede a dividir las Fs por el coeficiente R, para reducir los efectos sísmicos necesarios en las combinaciones de carga considerados en el diseño de los elementos estructurales sismorresistentes que componen a los modelos de base fija.

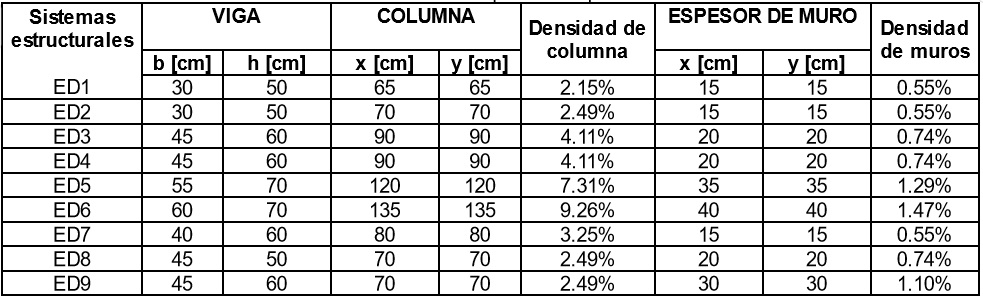
Los elementos que forman parte de la resistencia sísmica y de cargas verticales del sistema se diseñaron por capacidad DES, teniendo en cuenta los Capítulos C.7, C.8, C.9, C.10 y C.21 de la NSR-10 [5] y fueron asignados a los modelos de base flexible. En la Tabla 5 se resumen las secciones transversales de estos elementos, las cuales cumplieron con los análisis elástico-lineales, requisitos geométricos y de resistencia en el diseño establecidos en la NSR-10 [5].

Tabla 5 Sección transversal de elementos estructurales que forman parte de los sistemas del modelado.

2.5 Capacidad admisible del suelo

En el análisis de una cimentación se debe revisar la seguridad del terreno de apoyo, tanto de capacidad de carga por resistencia al corte como por deformaciones. Para esto, se debe extraer la solicitación en la base de cada una de las columnas que llegan al apoyo en el modelo de base fija, se evalúa la solicitación en capacidad en estas reacciones y se verifica que no excedan los estados límite de falla y de servicio del suelo de cimentación.

La capacidad de carga última por resistencia al corte del suelo se refiere a la presión vertical máxima que el suelo puede soportar sin que se produzca un fallo por corte. Este valor está relacionado con el desplazamiento plástico del suelo, tanto local o general del suelo bajo la cimentación. Para su cálculo en la presente investigación, se ha utilizado la formulación de Meyerhof, ya que genera valores adecuados al tener en cuenta la capacidad portante y factores de forma, profundidad e inclinación de la carga [36].

Por otro lado, la carga por servicio del suelo se refiere a la carga admisible que se tiene en cuenta para evitar un asentamiento excesivo del suelo ante una estructura en servicio. En este caso, se ha calculado utilizando la formulación de Bowles [37], la cual establece una relación entre la presión de carga y la resistencia a la penetración estándar. Se ha aplicado el criterio de asentamiento máximo recomendado desde la Ref. [36], que establece un límite de 50 [mm].

En la Figura 4 se presentan los rangos de las capacidades admisibles que se aplicaron a las distintas tipologías geométricas de las cimentaciones. Estas capacidades se evaluaron en el peor escenario posible, ya sea por resistencia (usando la formulación de Meyerhof [36]) o por servicio (asentamiento [37]), con el objetivo de garantizar que satisfagan la solicitación de toda la estructura sobre las reacciones en la base. Es importante destacar que los edificios ED5 y ED6 presentan valores fijos, ya que presentan una única tipología de cimentación.

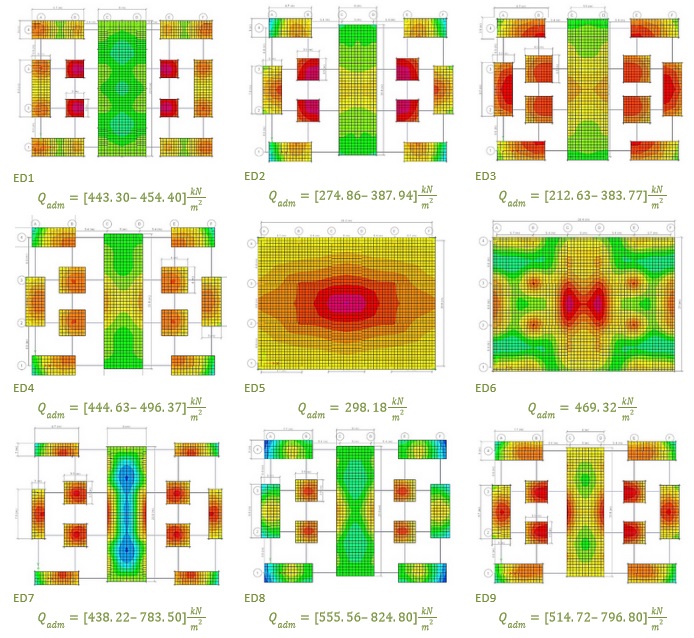
Figura 4 Capacidad admisible de los perfiles de suelo para cada tipo de cimentación de los sistemas del modelado.

2.6 Teoría de Winkler

Uno de los enfoques comunes para modelar la interacción entre la estructura, la fundación y la flexibilidad del suelo que soporta a esta es el enfoque de subestructura (método de Winkler [38] [20]), esta es una aproximación donde el suelo se representa como un resorte. En este proyecto se consideraron los resortes verticales, ya que esta orientación es comúnmente empleada para capturar la rotación, la cual suele ser un factor determinante en los efectos de la ISE [16]. Por otro lado, se fijaron los efectos de traslación, dado que no se tuvo en cuenta el amortiguamiento de la fundación.

Las funciones de impedancia de Winkler [20] [16] se refieren a la representación de la respuesta de una cimentación que se apoya en un suelo elástico y homogéneo, en el cual la deformación del suelo es proporcional a la carga aplicada. El modelado de esta respuesta se realiza mediante la consideración de la rigidez del suelo, la profundidad de la cimentación y la geometría de esta.

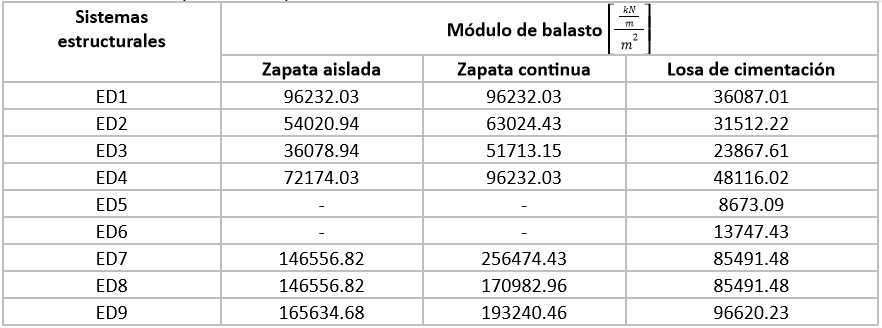
En la presente investigación el método adoptado fue el de fundación flexible y suelo linealmente flexible, este método define una distribución de resortes representativos del suelo portante como un medio continúo discretizado, con un valor uniforme de resortes a lo largo de la cimentación. Este fue el método utilizado ya que es el adecuado cuando se modelan elementos de la cimentación de manera explícita. Para calcular el coeficiente de resorte unitario de la subrasante (módulo de balasto) se usó la formulación de ASCE/SEI 41-17 [39]. Los valores de módulo de balasto obtenidos son los que se encuentran en la Tabla 6.

Tabla 6 Módulos de balasto para cada tipificación de estudio de los sistemas del modelado.

3. RESULTADOS Y ANÁLISIS DE RESULTADOS

---

3.1 Respuesta de periodo fundamental

En los sistemas muro-pórtico modelados y diseñados con base fija (sin ISE), se verificó que los periodos fundamentales estuvieran por debajo del permitido por normativa [5] y controlados para la implementación del método FHE. Los resultados serán interpretados mediante la clasificación de los edificios ED1–ED9 según el número de pisos. Aquellos con más de 15 pisos serán denominados edificios de mayor altura, mientras que los demás se considerarán de menor altura.

La Figura 5 presenta los periodos fundamentales obtenidos en los diferentes sistemas estructurales modelados como base fija. El periodo fundamental que proporciona la NSR-10 y el análisis de base fija dependen exclusivamente de la altura del edificio, como se indica en el estudio [40]. En este sentido, la figura muestra que los modelos ED2 a ED4 (suelo D) y ED8 a ED9 (suelo C) son los edificios más flexibles en relación con la altura, dado que presentaron una diferencia de periodo fundamental (∆T) respecto al periodo máximo definido por la normativa local inferior al 30%, en comparación con los demás edificios. Por otro lado, los modelos de baja altura sobre suelo D (ED1) y suelo C (ED7), junto con los de mediana altura sobre suelo D (ED5-ED6), se identifican como sistemas más rígidos (∆T≥30%).

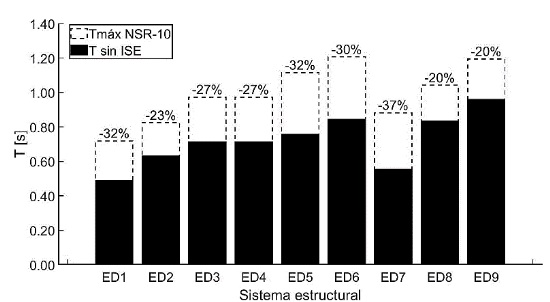
Figura 5 resultados de periodos fundamentales base fija.

Al considerar la flexibilidad de la base en los sistemas estructurales ED1 – ED9, se observó un aumento en los periodos fundamentales, como se ha encontrado en estudios similares [41]. Así mismo, estos periodos superaron los valores máximos recomendados por la norma (NSR-10 [5]), con la excepción del modelo ED7 (12 pisos sobre suelo C), como se muestra en la Figura 6. Esto se debe a que el edificio ED7 se apoya sobre un suelo medianamente rígido con velocidades cercanas a los 400 m/s, lo que lo convierte en un sistema rígido en altura y tipología de suelo. Por el contrario, el modelo ED2, que se define como un sistema flexible en el análisis de base fija, muestra un aumento en el periodo fundamental que supera en más del 25% al periodo máximo entre los edificios de baja altura al incluir la ISE. Lo anterior indica que el aumento del periodo fundamental se debe a la adición de la flexibilidad del suelo proporcionada por la ISE sobre la flexibilidad de altura contemplada en el análisis de base fija. Este efecto es más notable en los modelos ED5 y ED6, en los cuales se observa un mayor aumento en el periodo al ser sistemas de mediana altura sobre suelo flexible tipo D en comparación con el máximo permitido por la normativa.

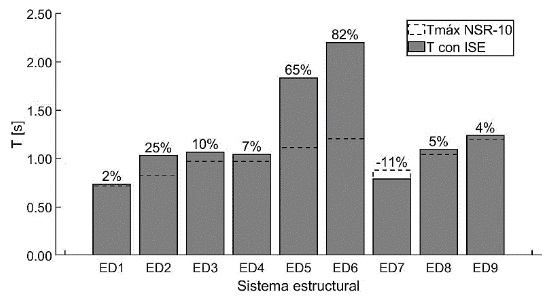
Figura 6 resultados de periodos fundamentales base flexible.

Al comparar la respuesta de los modelos de base fija (sin ISE) y de base flexible (con ISE) en la Figura 7, se observa que el incremento en los períodos fundamentales fue más notable en los sistemas estructurales de mediana altura, como los modelos ED5 y ED7 sobre suelo flexible, llegando a superar el 100%. Asimismo, los períodos fundamentales obtenidos para los modelos ED5 y ED6 sobre suelo tipo D con ISE superan el requisito de 2Tc=1.403s (A.3.4.2 de la NSR-10). Por lo tanto, en el análisis elástico lineal no es suficiente utilizar únicamente el método FHE, como se había previsto en el análisis de base fija, sino que es necesario incorporar el método de modal espectral. Por lo anterior, los resultados de la respuesta estructural lineal en relación con la deriva y cortante de base son los obtenidos por el análisis modal espectral.

También se observó que los períodos fundamentales para los modelos de base fija predominan en la dirección X, con una participación direccional del 68% - 70%, y en la dirección Y, con una participación del 70% - 72%. Estos resultados sugieren que el sistema de la

Figura 3 en un análisis de base fija es más sensible a las vibraciones sísmicas en la dirección Y. Sin embargo, al incorporar la ISE, los períodos fundamentales mantienen una mayor participación en la dirección X, salvo para los modelos ED5 y ED6 de mediana altura sobre suelo tipo D. Estos resultados concuerdan con otros estudios [42], que señalan que la incorporación de la ISE puede afectar el comportamiento sísmico de la estructura en su periodo fundamental y participación de masa. También se observó en este estudio que la participación direccional puede variar a medida que se aumente la altura y la velocidad de corte, considerando estos hallazgos relevantes y deben tenerse en cuenta en el diseño de los elementos.

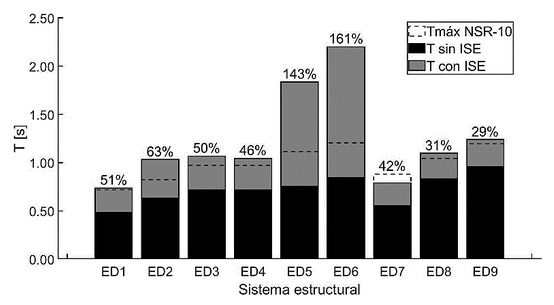
Figura 7 Periodo estructural y relación con base fija vs flexible.

En resumen, la incorporación de la ISE tuvo un impacto significativo en la respuesta de periodo fundamental de los sistemas estructurales analizados debido a la flexibilidad adicional inducida por el suelo. Los modelos de baja altura (ED1 a ED4 y ED8), inicialmente considerados más rígidos en el análisis de base fija, mostraron una respuesta estructural de periodo flexible. Es importante destacar que los modelos ED1 a ED4 están caracterizados por el mismo perfil de suelo (perfil D), pero presentan variabilidad en el incremento de la respuesta entre la base fija y la base flexible debido a diferentes valores de VS.

Los modelos ED2 y ED3, que se cimentan sobre suelos más flexibles con Vs≤271.11 m/s, muestran un mayor alargamiento del periodo en comparación con los edificios ED1 y ED4, que tienen velocidades de onda cercanas a los 360 m/s. Además, se observó que en los edificios construidos sobre suelos C también presentan cambios significativos en la respuesta estructural, excediendo alrededor de un 30% los obtenidos en base fija, haciendo necesario evaluarlos a pesar de que la normativa vigente advierte el alargamiento del periodo sobre suelos D, E y F. Por lo que sistemas estructurales de baja altura sobre suelo C y D también deben ser evaluados contemplando la ISE con el mismo interés que se analizan sistemas estructurales de gran altura como lo han recomendado estudios similares [43], ya que no sólo genera variación en la respuesta modal sino también en la metodología lineal a implementar.

3.2 Respuesta modal

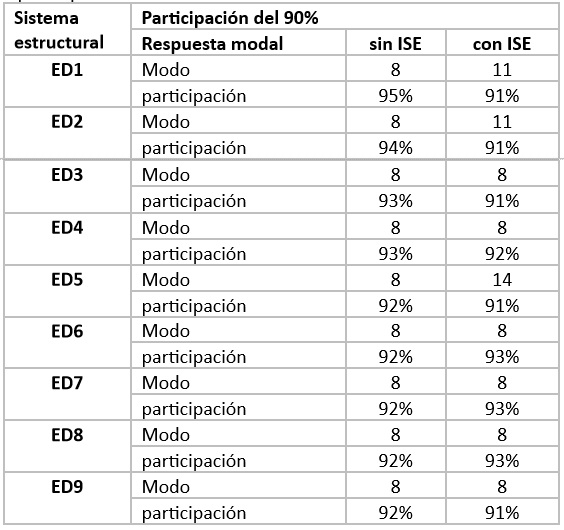
En todos los modelos de base fija, se observaron modos de vibración traslacionales con una participación de masa acumulada del 90% en el modo 8 para los edificios sobre perfil de suelo tipo D (ED1 – ED6) y C (ED7 – ED8). La Tabla 7 muestra que los sistemas de baja altura sobre suelo D (ED1 – ED4) tienen una mayor participación en comparación con los sistemas de mediana altura sobre suelo D (ED5 – ED7) y suelo C (ED8 – ED9). Al incluirse la ISE en los modelos de base fija, los modos de vibración traslacionales con participación de masa del 90% se mantuvieron en el modo 8 para los sistemas a excepción de aquellos con Vs < 324.5 m/s (ED1–ED3, ED5 y ED9), contando con mayor participación del orden del 93% en los edificios con suelos más rígidos (Vs≥324.5 m⁄s) y de mediana altura (ED4, ED6 – ED8). Encontrando que los sistemas con suelo flexible y de baja altura presentan mayor incidencia en la respuesta modal al incluir las propiedades mecánicas del suelo en comparación con su modelado de base fija.

Esta observación se sustenta al comparar la respuesta de los modelos ED3 y ED4, ya que, para un mismo tipo de sistema estructural sobre una similar clasificación de perfil de suelo (perfil D) pero velocidad cortante diferente (249.00 m/s y 324.50m/s) se presenta menor participación de masa a menor velocidad de onda de corte tal como lo presenta la Tabla 7.

Tabla 7 Modos en donde la participación de masa se dio al 90%.

3.3 Respuesta deriva máxima

En el modelo de base fija se verificó que las derivas en las direcciones X e Y cumplieran con el valor máximo permitido por la normativa del 1.0% (según el Artículo A.6.4 de la NSR-10 [5]), que se permite observar en la Figura 8. Es importante destacar que la rigidez de los elementos estructurales influye en la respuesta de la deriva, siendo los elementos más rígidos los que presentan menores derivas y menos rígidos los que presentan mayores derivas.

En este sentido, se puede identificar en la dirección X que los modelos con elementos estructurales menos rígidos fueron ED2 – ED4 y ED8 – ED9, medianamente rígidos ED5 – ED6 y rígidos ED1 y ED7. Evidenciando que los sistemas ED2 y ED7, se identifican como sistemas con mayor rigidez en cuanto a derivas, en comparación con los demás modelos.

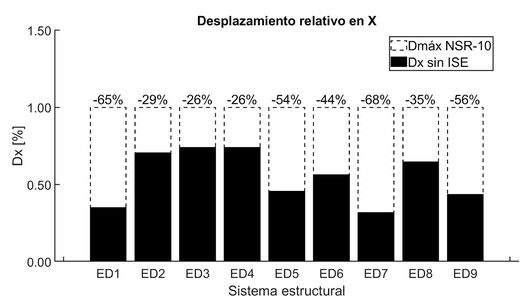
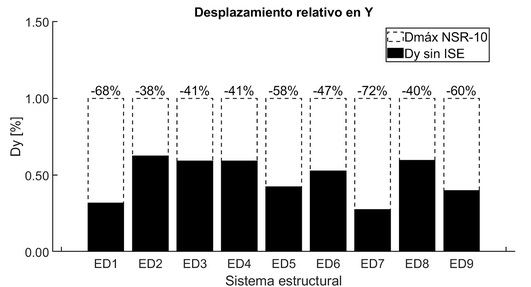
Figura 8 Desplazamientos relativos en X y Y base fija con modal espectral

Al incluir la ISE bajo la metodología de Winkler, se observó en la ¡Error! No se encuentra el origen de la referencia. que, aunque los sistemas estructurales controlaron el desplazamiento relativo durante el análisis de modelos de base fija y estuvieron por debajo del límite máximo establecido por la NSR-10 (1.0%), estos valores aumentaron. Sin embargo, esta condición solo se superó en los modelos más altos construidos sobre el perfil de suelo D (ED5 y ED6), como se presenta en otros estudios [44].

A partir de lo anterior, se puede observar que el aumento de la deriva se debe a la flexibilidad del edificio en relación con su altura, la cual se incrementa al incorporar las propiedades de la base de suelo. Este efecto es evidente en los sistemas ED5 y ED6. Además, se puede notar que los sistemas estructurales de baja altura tienen un mayor impacto en la respuesta de la deriva cuando están cimentados en suelos más flexibles (Vs<324.5 m/s) en comparación con aquellos construidos sobre suelos más rígidos.

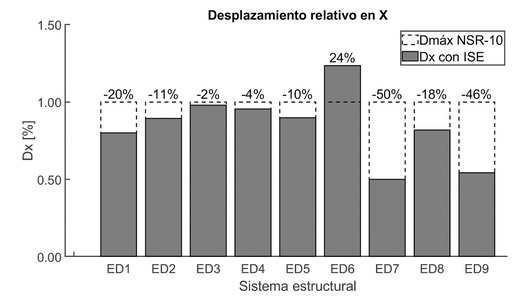
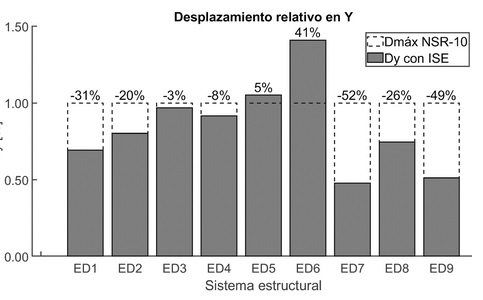
Figura 9 Desplazamientos relativos en X y Y base flexible.

En general, según los resultados presentados en la Tabla 7 y la respuesta de las derivas mostrada en la Figura 8, se observa una mayor participación direccional en respuesta de periodo fundamental y mayores derivas en la dirección X en comparación con la dirección Y.

En la Figura 10 se puede observar la respuesta de las derivas máximas de los modelos con ISE y sin ISE, donde se evidencia que los sistemas estructurales con mayor número de pisos construidos sobre suelo flexible (ED5 y ED6) superan la deriva máxima especificada por la NSR-10 y presentan una participación direccional de periodo fundamental en la dirección opuesta a la obtenida en el análisis de base fija.

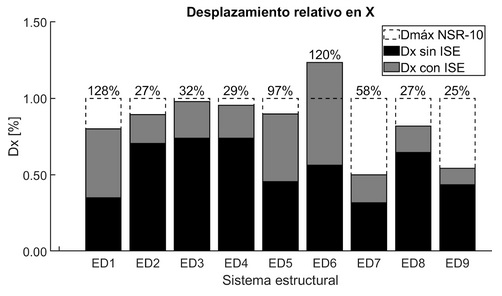
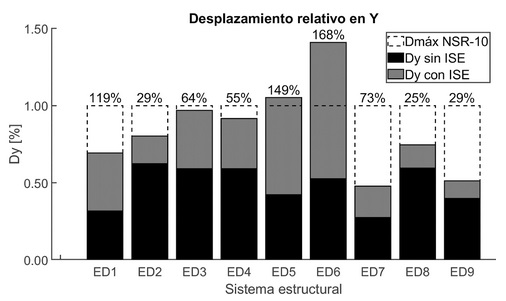
Figura 10 Desplazamiento relativo X y Y en relación con base fija vs flexible.

Por lo tanto, se puede afirmar que, al incluir la flexibilidad de la base, no solo se afectan los desplazamientos relativos, sino también la dirección predominante de estos movimientos debido al cambio en la participación modal. Además, se puede notar que los sistemas de baja altura construidos sobre suelos flexibles, como el modelo ED1, presentan un grado similar de impacto en la ISE en comparación con los modelos más altos construidos sobre suelos flexibles (ED5 y ED6) incrementando su respuesta por encima del 100%.

3.4 Respuesta de cortante basal

La respuesta del cortante basal está relacionada con la aceleración espectral obtenida del periodo fundamental, este parámetro es muy importante en la práctica del diseño sísmico. Al estar relacionado con el periodo, los modelos ED1 - ED9 presentados en la Figura 11, muestran nuevamente, que los sistemas ED5 - ED6 son más flexibles, ya que obtienen un cortante de base mucho mayor que los demás sistemas ED1 - ED4 y ED7 - ED9. En contraste, los sistemas más rígidos son aquellos con una altura inferior a los 15 pisos, es decir, el ED1 - ED2 (sobre perfil de suelo D) y el ED7 - ED8 (sobre perfil de suelo C).

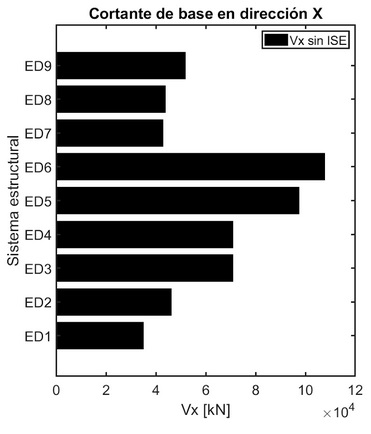
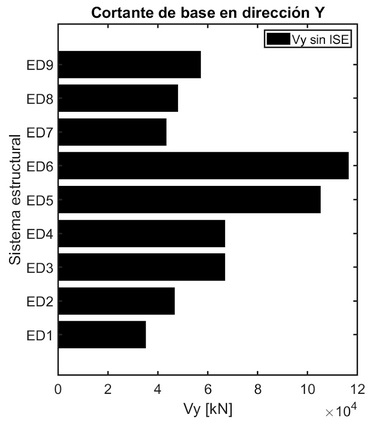
Figura 11 Cortante de base fija.

La Figura 12 muestra la respuesta del cortante basal de los modelos ED1 – ED9 con base flexible, donde se observó que a velocidades de onda mayores e incremento en el número de pisos, mayor cortante basal. Es decir, a medida que la flexibilidad del sistema es mayorada con el número de piso y velocidades de onda de corte se hace mayor su cortante de base.

Al comparar los sistemas ED2 y ED5 los cuales tienen suelo con Vs=271.11 m/s, el modelo de 12 pisos (ED2) presenta un cortante de base Vx^ED2=29521.81 kN y el modelo con 18 pisos (ED5) un Vx^ED5=49143.82 kN, presentándose en relación con su altura un incremento del 36% y 52%, respectivamente en el cortante de base. Ahora, para el caso de sistemas de igual altura ED3 y ED4, con velocidades de onda diferentes (249.00 m/s y 324.50m/s) hay un incremento de 36% para ambos sistemas en el cortante de base (Vx^ED3=44259.33 kN y Vx^ED4=45279.34 kN). Con lo anterior, se inferir que el número de pisos tiene una mayor incidencia en la flexibilidad del sistema en comparación con la velocidad del suelo, en lo que respecta a la respuesta de cortante de base.

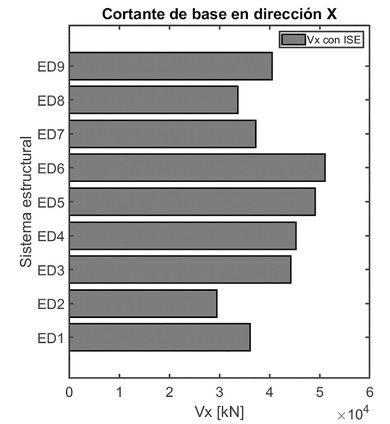
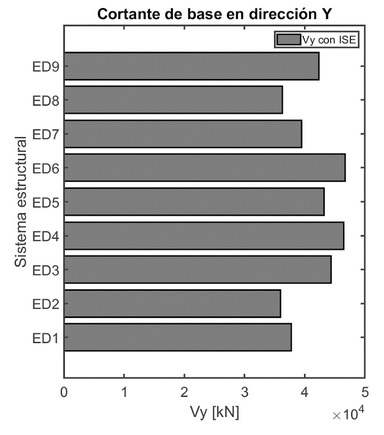
Figura 12 Cortante de base fija.

Finalmente, el alargamiento del periodo fundamental en sistemas de base flexible resulta en aceleraciones espectrales menores en comparación con los sistemas de base fija, lo que se evidencia en la Figura 13 a través de la disminución del cortante basal. Este efecto es más pronunciado en sistemas estructurales de mediana altura construidos sobre suelos flexibles, como se obtuvo en otros estudios [45].

Los modelos sobre base flexible (Vs < 324.5 m/s) son altamente favorecidos en la disminución de cortante basal en el caso de los modelos de base más rígida. Lo anterior, debido a que al tener en cuenta no solo la flexibilidad proporcionada por la altura sino la flexibilidad del suelo, se permite una capacidad de deformación mayor ante cargas laterales.

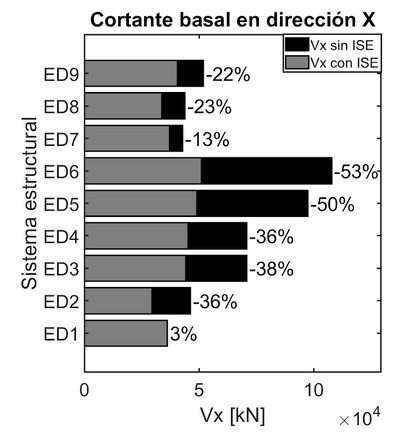
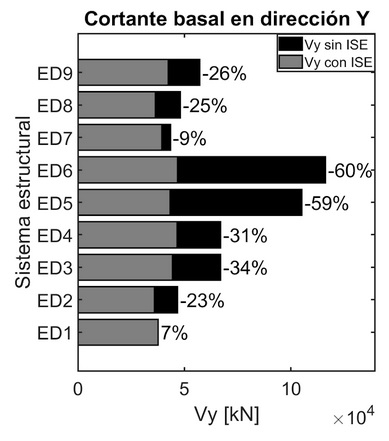
Figura 13 Cortante de base y relación con base fija vs flexible.

4. CONCLUSIONES

---

Esta investigación evaluó la influencia de la Interacción Suelo-Estructura (ISE) a través del enfoque simplificado de subestructura propuesto por Winkler [17] en sistemas estructurales muro-pórtico regulares representativos de Bucaramanga. Los edificios estudiados fueron artificiales y su geometría se definió a partir de información obtenida del mapeo de estructuras de esta tipología ubicadas en dicha ciudad. También se utilizaron registros de velocidades de onda de corte para estimar la rigidez del suelo. En total se analizaron 9 edificios artificiales, variando el tipo de suelo y el número de niveles en altura. Finalmente, para los modelos con y sin ISE, se compararon las respuestas estructurales como desplazamientos laterales, periodo fundamental, aceleraciones, corte basal y participación de masa.

De acuerdo con el trabajo presentado, se pueden extraer las siguientes conclusiones

• *Los modelos sobre suelos de fundación tipo C y D sin exclusión de altura, es necesario evaluarlos incluyendo la ISE, ya que exceden el periodo fundamental recomendado por la normativa. Los periodos fundamentales de los edificios al incluir ISE fueron mayores al límite establecido por el código colombiano. En el escenario más desfavorable, el incremento presentado fue de 82%, lo cual evidencia la necesidad de considerar la flexibilidad de suelos blandos (tipo C y D) en el cálculo de la respuesta dinámica de edificios entre 10 y 20 niveles.
• *Los sistemas estructurales de altura menor a 15 pisos tienen un mayor impacto en la respuesta de la deriva cuando están cimentados en suelos más flexibles (Vs < 324.50 m/s) , en comparación con los que se construyen sobre suelos más rígidos. Esto se debe a que la flexibilidad del suelo, combinada con la altura del edificio, puede causar una mayor deformación ante cargas laterales, lo que resulta en una respuesta de deriva más pronunciada. Se presentan incrementos hasta del 85% en edificios de altura menores a 15 pisos y 149% en edificios de alturas superiores.
• *Los sistemas estructurales de altura menor a 15 pisos que se encuentran construidos sobre suelos flexibles tienen mayor incidencia en la respuesta modal, ya que al considerar las propiedades mecánicas del suelo en su modelado se presentan cambios en el modo de vibración donde se concentra el 90% de la masa acumulada en comparación con el modelado sobre un suelo más rígido, lo que puede acaparar problemas en la respuesta direccional del sistema y el diseño de los elementos.
• *Se puede notar que el número de pisos tiene una mayor influencia en la flexibilidad del sistema en comparación con la velocidad del suelo, en lo que respecta a la respuesta de cortante de base. Esto genera una reducción del cortante por encima del 50%, lo que indica que el diseño de la estructura y la selección del número de pisos pueden ser incidir en la reducción del cortante basal.
• *Los períodos fundamentales en sistemas estructurales altos sobre suelo superan el requisito de 2Tc=1.403s (A.3.4.2 de la NSR-10). Por lo tanto, en el análisis elástico lineal, no se puede utilizar únicamente el método de Fuerza Horizontal Equivalente (FHE), sino que es necesario incorporar el método de modal espectral.
• *Los modelos sobre perfil de suelo C presentan incrementos que exceden el referido por la norma, a pesar de que la NSR-10 advierte el alargamiento del periodo sobre suelos D, E y F. Cabe resaltar que los perfiles de suelos C también presentan cambios en la respuesta estructural excediendo los límites normativos.
• *Al incluir la flexibilidad de la base, no solo se afectan los desplazamientos relativos, sino también la dirección traslacional predominante de estos movimientos, lo que podría generar imprecisiones direccionales en el análisis sísmico de base fija.
• *Los sistemas de altura inferior a 15 pisos, construidos sobre suelos flexibles presentan un grado similar de impacto de la ISE en comparación con los modelos más altos construidos sobre suelos flexibles.
• *Los sistemas con mayor índice de significancia de la ISE evaluadas con la formulación de lA Agencia Federal para el Manejo de Emergencias (FEMA), pueden evidenciar que es acertada en cuanto a la respuesta a priori de la inclusión de la ISE. Ya que el modelo ED7 y ED8 presentaban una probabilidad cercana al límite de 0.10 las cuales exhibieron menor significancia en las respuestas estructurales elásticas lineales.
• *Como lo describe el estudio de Ref. [46], el periodo fundamental aumenta con el incremento de la rigidez de resortes o módulo de balasto.
• *Los resultados obtenidos en esta investigación presentan y confirman que el papel de la interacción en la respuesta estructural presenta aumento del periodo fundamental, cambio de deflexiones laterales y amplificación de las derivas del suelo como lo especifica el estudio [47]. Por lo que se puede prever que no incorporarlo en el análisis estructural podría afectar en la respuesta exacta en cuanto al rendimiento sísmico. Por lo que se pretende continuar el estudio incorporando técnicas de confiabilidad estructural para evaluar la probabilidad de falla de estos sistemas.

En general, las respuestas estructurales de un sistema muro-pórtico se ven afectadas por la interacción suelo-estructura modelada utilizando el enfoque de Winkler. Las observaciones indican que el efecto de la ISE debe incorporarse en el caso del suelo blando, de lo contrario, podría conducir a una mala precisión. Además, el análisis paramétrico variando la altura y el tipo de suelo de fundación, con y sin ISE, reveló que las estructuras de altura mayor a 15 pisos se ven más afectadas por ISE que las estructuras altura inferior a 15 pisos. Entre menor sea su velocidad de onda Vs < 360 m/s mayor incidencia tiene en la respuesta estructural de periodo estructural, deriva y cortante de base. Se recomienda incluir la implementación de estudios adicionales como el cálculo de daño a través de técnicas de confiabilidad estructural teniendo en cuenta el parámetro más común en el análisis de vulnerabilidad como lo es los desplazamientos relativos e incluir análisis de segundo orden en la respuesta de los elementos estructurales bajo las fuerzas laterales obtenidas al incluir la flexibilidad de la base.

5. AGRADECIMIENTOS

---

Deseo expresar mi más profundo agradecimiento a todas las personas que han colaborado y apoyado el desarrollo de esta investigación. En especial, quiero reconocer y agradecer a mis directores y distinguidos colegas quienes han brindado una guía invaluable en el aprendizaje de este fascinante campo de la ingeniería estructural. Asimismo, deseo expresar mi gratitud a la Universidad Industrial de Santander por proporcionar las instalaciones y recursos necesarios para llevar a cabo esta investigación de manera exitosa. Una vez más, les agradezco por su apoyo y compromiso con este proyecto, cuyo impacto en el campo de la ingeniería estructural será de gran relevancia.

6. REFERENCIAS BIBLIOGRÁFICAS

---