OPTIMIZACIÓN DE ISOTERMAS DE ADSORCIÓN MEDIANTE SIMULATED ANNEALING

Jorge Orlando Pellerini¹; Jorge Pablo de Celis²

RESUMEN

El presente trabajo estudia el ajuste de los datos experimentales de las isotermas de adsorción en un sistema de cromo hexavalente como adsorbato y carbón activado como adsorbente. Los ensayos de adsorción consistieron en poner en contacto 0,1 gramo de adsorbente con soluciones de diferente concentración de cromo hexavalente durante 48 h a distintas temperaturas. Para el modelado se propuso un método distinto al tradicional, mediante el cual se optimiza la energía de activación de la adsorción de manera que se generen las contantes de equilibrio que minimicen el error cuadrático medio respecto a los datos experimentales. Para ello, se empleó Simulated Annealing como algoritmo de optimización. Una temperatura inicial de 1000, 10000 iteraciones y un tamaño de paso de 0,05 fueron los parámetros utilizados. Ambos métodos presentan ajustes adecuados, mostrando energías de activación del mismo orden. Esto indicaría que el algoritmo de optimización sería comparable a los procedimientos tradicionales.

Palabras claves: adsorción; isoterma; carbón activado

Recibido:11 de Abril de 2023. Aceptado: 4 de Agosto de 2023

Received:April 11, 2023. Accepted:August 04, 2023

OPTIMIZATION OF ADSORPTION ISOTHERMS BY SIMULATED ANNEALING

ABSTRACT

The present work studies the adjustment of the experimental data of the adsorption isotherms in a system of hexavalent chromium as adsorbate and activated carbon as adsorbent. The adsorption tests consisted of using 0.1 gram of adsorbent with solutions of different concentrations of hexavalent chromium for 48 h at different temperatures. For the modeling, a method different from the traditional one was proposed, where the adsorption activation energy is optimized to generate the equilibrium constants that minimize the mean square error with respect to the experimental data. For this, Simulated Annealing was used as the optimization algorithm. An initial temperature of 1,000, 10,000 iterations, and a step size of 0.05 were the parameters used. Both methods present adequate adjustments, showing activation energies of the same order. This would indicate that the optimization algorithm would be comparable to traditional procedures.

Keywrods: adsorption; isotherm; activated carbon

Cómo citar este artículo: J. Pellerini, J. Celis. “Optimización de isotermas de adsorción mediante Simulated Annealing”, Revista Politécnica, vol.19, no.38 pp.30-37, 2023. DOI:10.33571/rpolitec.v19n38a2

1. INTRODUCCIÓN

---

Actualmente, la contaminación debida a los desechos industriales de efluentes que contienen iones de metales pesados representa un problema ambiental grave, tanto para la flora y fauna como también a la disponibilidad de agua de consumo humano [1,2].

Entre los metales pesados presentes en los efluentes, se destaca el cromo hexavalente debido a su efecto cancerígeno y su impacto a diversos organismos acuáticos [3]. Existen diferentes técnicas para el tratamiento de un efluente con este contaminante como la precipitación química, extracción con solventes, intercambio iónico, adsorción, oxidación, filtración de membrana, entre otros [4,5,6,7]. Entre estas técnicas, se destaca la adsorción debido a su simplicidad, bajo costo, buena eficiencia de remediación y disponibilidad de materiales adsorbentes [8,9].

La adsorción de cromo hexavalente ha sido estudiada con diversos adsorbentes, como los nanomateriales [10] y el carbón activado [11]. El carbón activado (CA) presenta una alta efectividad en la remoción del cromo hexavalente debido a su alta superficie específica y a la presencia de sitios activos donde sucede el proceso de adsorción [12].

El presente trabajo plantea un procedimiento alternativo en el cálculo de las isotermas de adsorción para el sistema Cr(VI)-CA.

2. MATERIALES Y MÉTODO

---

2.1. Síntesis del adsorbente

El carbón activado (CA) es sintetizado mediante un proceso de activación química empleando un residuo agroindustrial como precursor lignocelulósico. En este trabajo se empleó cáscara de nuez, que fue acondicionada a un tamaño inferior a los 0,5 mm. Este precursor se sometió a un proceso de impregnación con una solución al 50% m/m de H3PO4 y en una relación 2/1 (ácido/precursor). Luego, se sometió el material impregnado a un proceso de calentamiento a 110ºC durante 2 horas en estufa. Posteriormente, en una mufla, se procedió a la carbonización de la muestra mediante una rampa de calentamiento hasta alcanzar los 400ºC. Esta temperatura se mantuvo durante una hora. Finalmente, luego del proceso de enfriamiento hasta alcanzar la temperatura ambiente, el carbón activado obtenido fue lavado con agua desionizada hasta verificar la ausencia de restos del ácido empleado.

2.2. Experimentos de adsorción

Se emplea 0,1 g de carbón activado por ensayo, pesado en balanza analítica con una precisión de 0,0001 g. El volumen de solución empleado es de 100 ml, medido con matraz aforado.

Para el comienzo del proceso de adsorción, se pone en contacto el carbón activado con soluciones de diferentes concentraciones de cromo hexavalente (preparadas a partir de dicromato de potasio y agua) con una agitación continua.

Transcurrido un tiempo de 48 horas, suficiente para que el sistema alcance el equilibrio, se filtraron las muestras para analizar el contenido de Cr(VI) presente en el filtrado. Las concentraciones iniciales y finales del contaminante modelo se cuantificaron mediante espectrofotometría UV-visible [13].

Los ensayos fueron realizados por duplicado y a distintas temperaturas de trabajo.

Para evaluar la cantidad de adsorbato removido, se define la capacidad de adsorción:

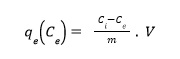(1)

Siendo Ci [ppm] y Ce [ppm] la concentración de cromo hexavalente inicial y en el equilibrio respectivamente, m [g] es la masa de carbón activado, V [L] es el volumen de la solución y qe [mg.g-1] es la capacidad de adsorción.

2.3. Equilibrio del proceso de adsorción

Las isotermas de adsorción relacionan la capacidad de adsorción del adsorbente con la concentración de equilibrio. Se puede interpretar como la relación de la cantidad de adsorbato adsorbida y la que permanece en solución una vez que el sistema llegó al equilibrio a una temperatura dada [14]. En este trabajo, se empleó el modelo de Langmuir [15], que es utilizado frecuentemente en el campo de estudio [16,17,18].

El modelo asume una adsorción en monocapa que contiene una cantidad de sitios activos finitos de energía uniforme [18].

La ecuación de la isoterma de Langmuir es:

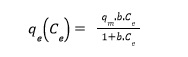(2)

donde: qe [mg.g-1] es la capacidad de adsorción, qm [mg.g-1] es la capacidad de adsorción máxima de mono capa, b [L.mg-1] es la constante de equilibrio y Ce [ppm] es la concentración de equilibrio del adsobato. La constante b es única para una temperatura determinada, su variación respecto a la temperatura responde a la ecuación de Arrhenius:

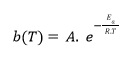(3)

donde: A [L.mg-1] es el factor pre exponencial, Ea [Kj.mol-1]es la energía de activación, R es la constante universal de los gases [Kj.mol-1] y T [K] es la temperatura absoluta.

La metodología tradicional consiste en ajustar los datos a la ecuación 2 para cada temperatura. Posteriormente, se ajusta los valores de b a la ecuación 3 para obtener la energía de activación. Los ajustes se hacen a partir de las formas lineales de las ecuaciones 1 y 3:

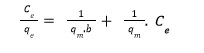(4)

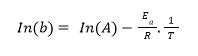(5)

siendo 4 y 5 las ecuaciones lineales de las ecuaciones 2 y 3 respectivamente.

2.4. Simulated Annealing

El método propuesto consistió en realizar una serie de iteraciones, variando los parámetros a optimi-zar de forma aleatoria (perturbación) [19]. Para cada iteración, se evaluó la función objetivo (conocida también como error del sistema), empleando un criterio de aceptación predeterminado de cada nueva solución obtenida una vez perturbados los parámetros. Este criterio aceptó la nueva solución si el error del sistema disminuye respecto al resultado de la iteración anterior. Además, se incluyó el criterio de aceptar una solución peor, con una probabilidad de aceptación que disminuye a lo largo de las iteraciones. El algoritmo se exhibe en la ecuación 6, donde se muestra el cálculo de la probabilidad de aceptación para la solución perturbada [20].

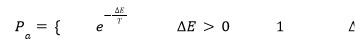(6)

donde: ∆E es la diferencia entre el error antes y después de la perturbación de los parámetros a optimizar. T [adimensional] es la temperatura del algoritmo que va modificándose a través de las iteraciones, controlando que la probabilidad de aceptar una peor solución disminuya con las iteraciones.

La regla de actualización de la temperatura es:

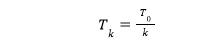(7)

siendo: Tk [adimensional] la temperatura en la iteración k, To [adimensional] es la temperatura inicial y k el número de iteraciones.

Las variables a optimizar son:

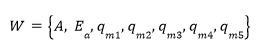(8)

donde: qmn es la capacidad de adsorción máxima de mono capa para las distintas n temperaturas ensayadas.

La perturbación de W se muestra en la ecuación 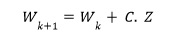9:

(9)

donde: k+1 y k representa la realización de una iteración en el algoritmo, C se define como el tamaño del paso y Z es un vector de la misma longitud que W de valores aleatorios con una distribución gaussiana de media 0 y varianza 1.

2.5. Función objetivo

La Función objetivo propuesta se muestra en la ecuación 10. Representa el error cuadrático medio entre los datos y la salida de las isotermas de Langmuir para cada temperatura.

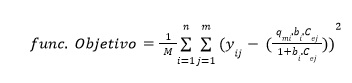(10)

donde: m son los datos por cada n isotermas. M es la cantidad de datos totales.

3.RESULTADOS

---

Los resultados experimentales para las distintas isotermas de equilibrio obtenidas se muestran en la Figura 1, los experimentos fueron realizados a las temperaturas de 4, 10, 20, 30 y 37ºC.

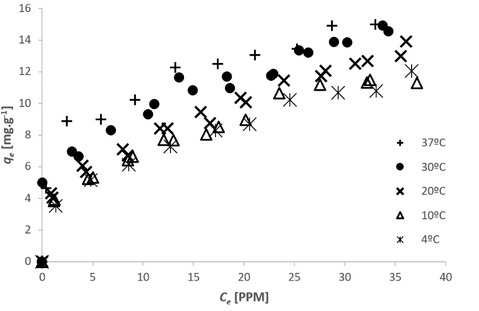
Figura 1. Isotermas de adsorción a diversas temperaturas.

Una vez aplicado el algoritmo optimizador, se observa en la Figura 2, la evolución del error cuadrático medio en función de las iteraciones. Se empleó una temperatura inicial de 1000 con un tamaño de paso de 0,05.

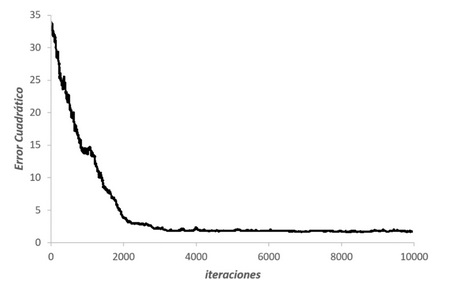
Figura 2. Error cuadrático medio en función de las iteraciones empleando el algoritmo SA.

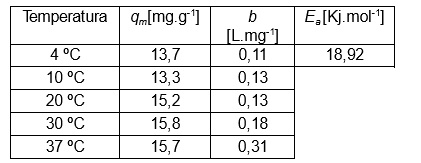
Los valores obtenidos de W se muestran en la Tabla 1. Por otro lado, en la Tabla 2 se exhiben los resultados obtenidos empleando la metodología tradicional. El error cuadrático medio estimado para el método propuesto es 1,500 mientras que para el método tradicional es 1,382.

Tabla 1. Valores obtenidos de las variables optimizadas por Simulated Annealing y valores correspondientes a las constantes de equilibrio.

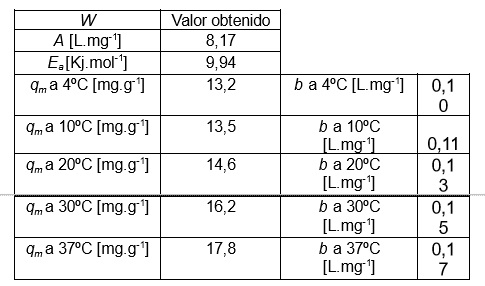
Tabla 2. Resultados del ajuste tradicional

En la Figura 3, se muestran los resultados de ambos métodos puestos en forma comparativa.

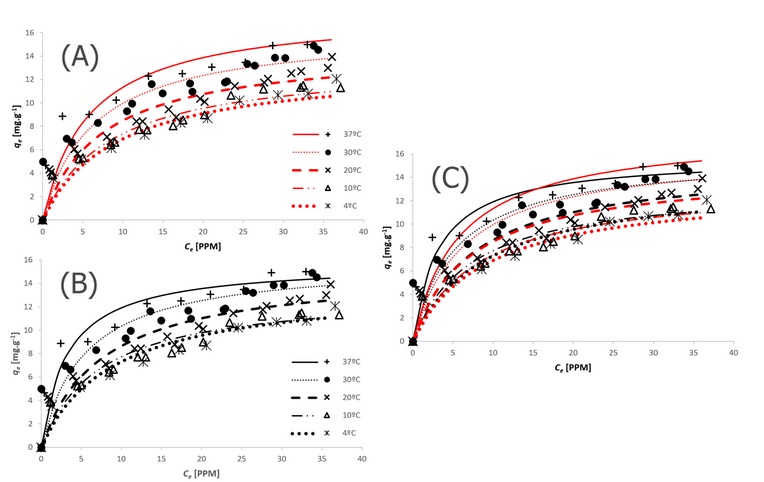
Figura 3. Resultados de las isotermas del (A) método propuesto, (B) método tradicional y (C) ambos.

4. DISCUSIÓN

---

La Figura 1 muestra como el proceso de adsorción es endotérmico, debido a que la capacidad de adsorción aumenta con la temperatura.

En la evolución de la Función Objetivo durante la implementación de SA (Figura 2) se puede apreciar la existencia de mínimos locales cuando la función se perturba en torno a un mismo valor para luego incrementarse y posteriormente decrecer a un nuevo mínimo. La Ecuación 6 y 7 exhiben como la probabilidad de aceptar una peor solución disminuye al aumentar las iteraciones, esto se puede apreciar más claramente en la Figura 2 una vez que se incrementan las iteraciones del algoritmo.

Los errores cuadráticos medios de ambas metodologías son similares, lo que sugiere que es satisfactorio el uso de SA. Sin embargo, se presentan diferencias en los parámetros obtenidos. Los valores de la capacidad de adsorción máxima son similares, destacando que el modelo propuesto es más consistente en el comportamiento endotérmico del sistema (qm aumenta con la temperatura). Respecto a los valores de b, se encuentran en el mismo orden. No obstante, para el modelo por SA presentan incrementos más suaves. Esto sucedería porque los valores de b tienen que responder a la Ecuación 3. Mientras que para el método tradicional no existe tal restricción, lo que ocasiona que pueda existir una incidencia de la naturaleza de los datos. Este análisis permite apreciar que el modelo propuesto alcanza el ajuste haciendo cambios tanto en b y en qm, provocando así una evolución ordenada y suave de las isotermas de equilibrio (Figura 3A). Mientras que el ajuste tradicional es por isotermas, de esta manera puede existir cambios más bruscos de una isoterma a otra. Por lo dicho anteriormente, esto explica la diferencia existente entre las energías de activación.

5. CONCLUSIONES

---

En el presente trabajo, se optimizaron las isotermas de adsorción mediante un planteo innovador. Se alcanzaron resultados comparables, ya que el error cuadrático medio y las energías de activación resultaron ser similares.

Para futuros trabajo se buscarán otras alternativas respecto al optimizador para poder comparar las técnicas y la viabilidad de la metodología propuesta en el trabajo. Y también, probar esta estrategia para otros conjuntos de datos que brindaría información en qué tanto representativo es el planteo del presente trabajo en el campo de la adsorción.

6. REFERENCIAS BIBLIOGRÁFICAS

---