IDENTIFICACIÓN DE CANDIDATOS A PRIMOS DE MERSENNE MEDIANTE CLASIFICACIÓN OVA-ANGULAR UTILIZANDO APRENDIZAJE AUTOMÁTICO CON REGRESIÓN SVM Y KERNEL GAUSSIANO

Y. Acevedo¹, G. Loaiza²

RESUMEN

En este artículo se presentan tres números primos como altos potenciales para ser números de Mersenne y se sugiere su aplicación en testeos computacionales de primalidad. Estos números son construidos a partir de un algoritmo de regresión fundamentado en máquinas de vectores de apoyo (Support vector machine - SVM) y usando un Kernel Gaussiano. El entrenamiento de datos se lleva a cabo mediante el lenguaje de programación de Phyton, En el estudio se abordan los datos actuales de primos de Mersenne y se trabaja con el grupo de clasificación Ova-angular para primos de Mersenne ℸ₃₁.

Palabras clave: Rotaciones Ova-angulares, Primos de Mersenne, Aprendizaje Automático, Máquinas de Vectores de Soporte (SVM), Kernel Gaussiano.

Recibido: 26 de enero de 2023. Aceptado: 26 de febrero de 2023

Received: January 26, 2022. Accepted: February 26, 2023

IDENTIFICATION OF MERSENNE PRIME CANDIDATES THROUGH OVA-ANGULAR CLASSIFICATION USING MACHINE LEARNING WITH SVM REGRESSION AND GAUSSIAN KERNEL

ABSTRACT

In this paper three prime numbers are presented as high potentials to be Mersenne numbers and their application in computational primality testing is suggested. These numbers are constructed from a regression algorithm based on Support vector machines (SVM) and using a Gaussian Kernel. Data training is carried out using the Phyton programming language, In the study we address the current data of Mersenne primes and work with the Ova-angular classification group for Mersenne primes ℸ₃₁.

Keywords: Ova-angular rotations, Mersenne’s primes, Machine Learning, Support Vector Machine (SVM), Gaussian Kernel.

Cómo citar este artículo: Acevedo, Y., Loaiza, G. (2023). “Identificación de candidatos a primos de mersenne mediante clasificación ova-angular utilizando aprendizaje automático con regresión SVM y Kernel Gaussiano” Revista Politécnica, 19(37), 102-110.
https://doi.org/10.33571/rpolitec.v19n37a7

1. CONTEXTUALIZACIÓN

---

La Inteligencia Artificial (IA) es una rama de la informática que busca crear sistemas capaces de realizar tareas que requieren inteligencia humana, como el razonamiento, la percepción o el aprendizaje. Dentro de la IA, el Machine Learning (ML) es una técnica que permite a los ordenadores aprender de datos, sin ser programados explícitamente, y mejorar su rendimiento en una tarea específica a medida que se exponen a más información [1].

Uno de los algoritmos de Machine Learning más utilizados en la actualidad es el Support Vector Machine (SVM). Este algoritmo es especialmente adecuado para problemas de clasificación y regresión, y se basa en la idea de encontrar un hiperplano que separe las diferentes clases de datos. SVM es especialmente útil cuando se trabaja con conjuntos de datos complejos [2] y de alta dimensión, y puede ayudar a encontrar patrones y relaciones en los datos que de otra manera podrían pasar desapercibidos.

Acorde con [3], la importancia de los algoritmos SVM en el contexto actual radica en su amplia gama de aplicaciones en campos como la medicina, la seguridad, la detección de fraudes, la predicción de precios y la clasificación de imágenes, entre otros. SVM es una herramienta poderosa que puede ayudar a los investigadores y profesionales a tomar decisiones informadas y precisas basadas en datos, lo que puede mejorar la eficiencia y la calidad de los resultados en una variedad de campos.

El kernel Gaussiano, también conocido como kernel RBF (Radial Basis Function), es uno de los kernels más utilizados en el algoritmo SVM para regresiones. Este kernel tiene la capacidad de transformar los datos de entrada a un espacio de alta dimensionalidad, permitiendo encontrar un hiperplano de separación que maximice la separación entre las clases y minimice el error de la predicción [4,5]. La importancia del kernel Gaussiano radica en su flexibilidad para ajustarse a diferentes formas de distribución de datos y su capacidad para manejar datos no lineales, lo que lo hace una herramienta valiosa en problemas de regresión en los que se requiere una alta precisión en la predicción.

El kernel Gaussiano también permite controlar la complejidad del modelo a través del parámetro de regularización C, lo que evita el sobreajuste o subajuste del modelo. Además, este kernel se puede interpretar como una medida de similitud entre dos puntos, lo que significa que los puntos cercanos en el espacio de entrada tendrán una mayor influencia en la predicción final. Esto hace que el kernel Gaussiano sea especialmente útil en problemas en los que los datos tienen una estructura de clusterización o regresión compleja, ya que puede capturar la variabilidad en cada cluster y mejorar la precisión de la predicción [6].

De esta manera el kernel Gaussiano es una herramienta poderosa en el algoritmo SVM para regresiones debido a su flexibilidad, capacidad de manejar datos no lineales y su habilidad para controlar la complejidad del modelo, lo que permite obtener una alta precisión en la predicción en una variedad de problemas de regresión.

Por otra parte, los números primos han sido un tema de estudio fascinante durante cientos de años. Además de su importancia en la teoría de números, también tienen aplicaciones vitales en campos como la criptografía y la seguridad informática [7,8]. En particular, los números primos grandes son esenciales para garantizar la seguridad en los sistemas de encriptación. Según el matemático Andrew Granville "la criptografía moderna depende crucialmente de los números primos grandes" [9].

Los números primos más grandes que se tienen a la fecha son los primos de Mersenne y su lista aún dista bastante de llegar a los 100, su principal motivo son los altos tiempos computacionales para testear su primalidad.

Revisar si un número de la forma 2^ρ-1 es primo, con ρ primo, puede durar la velocidad de procesamiento de la computadora que se utiliza para hacer el test y la disponibilidad de recursos de la red de voluntarios. En general, los números primos de Mersenne de grado elevado pueden tardar varios meses o incluso años en ser probados completamente. Por ejemplo, el número primo de Mersenne más grande conocido actualmente (2^82589933 - 1), que tiene 24.862.048 dígitos decimales y fue descubierto en diciembre de 2018, tardó más de dos años en ser probado por un equipo de voluntarios del proyecto GIMPS.

Bajo este contexto, es claro que verificar la primalidad de un número de Mersenne requiere tiempo y recursos significativos, sin embargo, la búsqueda de primos de Mersenne sigue siendo importante. Y. Acevedo en [10], presentó las rotaciones Ova-Angulares de un número primo mediante las congruencia modular 360:

ρ≡ℸ_ρ Mod(360),

De igual en [11], se presenta una clasificación para los primos de Mersenne en grupos disjuntos, lo que puede ayudar a los investigadores en una mejoría en sus esfuerzos de búsqueda para estos números considerando estos números en una partición de subgrupos disjuntos dos a dos y no como un todo.

Los grupos disjuntos entre sí de los primos de Mersenne están dados por la partición

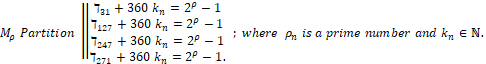
Y cada ρ_n primo, pertenece también a un conjunto de generación disjuntos uno a uno.

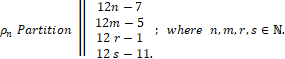
En este artículo, el estudio se centra en la primera partición (ℸ₃₁con primos exponentes de la forma 12n-7), dado que en la lista de los 51º primos de Mersenne M_ρn se tiene la mayor cantidad de datos asociados a este único conjunto, una mayor presencia y una cantidad considerable en relación a las otras 3 particiones que permite consolidar un conjunto de entrenamiento y prueba para la construcción de un modelo de regresión mediante SVM.

Tomando en consideración primos de Mersenne M_ρn y cuyo exponente la forma 12n-7=ρ_n, se hace posible establecer el siguiente conjunto de datos, que en adelante llamaremos lista “e”:

e=[5,17,89,521,4253,9689,9941,11213,19937,21701,859433,1398269,2976221,3021377,6972593,32582657,43112609].

Nótese que este es un subconjunto de la lista formada por todos los primos de Mersenne y aprovechando el hecho que es una partición de números primos en una secuencia no conocida, se buscará establecer una Regresión con Kernel Gaussiano para esta secuencia de datos y se estimarán los siguientes datos que estarían en la lista “e”.

2. DESCRIPCIÓN Y DESARROLLO

---

Para encontrar el valor óptimo de los parámetros del modelo, se utiliza la técnica de búsqueda de cuadrícula (GS- grid search) en combinación con validación cruzada. Esto implica a su vez, dividir los datos en conjuntos de entrenamiento y prueba, ajustar el modelo con diferentes valores de los parámetros y evaluar su rendimiento en el conjunto de prueba. Luego, se seleccionan los valores de los parámetros que producen el mejor rendimiento en el conjunto de prueba. Una vez que se tiene el modelo entrenado, ajustado y refinado, se emplea para predecir los tres posibles números primos en la secuencia de la lista “e”.

A continuación, se describe los pasos más fundamentales, con sus respectivos comandos, ejecutados en el lenguaje de programación de Python.

Primero se debe importar las bibliotecas necesarias y cargar los datos de la lista “e”:

Python
import numpy as np
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.svm import SVR
# cargar datos
e = [5,17,89,521,4253,9689,9941,11213,19937,21701,859433,1398269,2976221,3021377,6972593,32582657,43112609]
X = np.array(e[:-2]).reshape(-1, 1)
y = np.array(e[2:])

A continuación, se dividen los datos en conjuntos de entrenamiento y prueba:

Python
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Luego, se define una cuadrícula de parámetros para buscar el valor óptimo de los parámetros del modelo:

Python
param_grid = {'C': [0.1, 1, 10, 100, 1000],
'gamma': [1e-3, 1e-2, 1e-1, 1, 10, 100]}

A continuación, se inicia un modelo SVR con un kernel gaussiano:

Python
svr = SVR(kernel='rbf')

Luego, se utiliza una búsqueda de cuadrícula con validación cruzada para ajustar los parámetros del modelo:

Python
grid_search = GridSearchCV(svr, param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=-1)
grid_search.fit(X_train, y_train)

Una vez que se haya completado la búsqueda de cuadrícula, se puede imprimir los valores de los mejores parámetros y el error cuadrático medio en el conjunto de prueba:

Python
print("Better parameters: ", grid_search.best_params_)
print("Root mean square error in the test set: ", -grid_search.score(X_test, y_test))

Con los mejores parámetros encontrados, se procede a entrenar un modelo SVR con un kernel gaussiano en todo el conjunto de entrenamiento:

Python
best_svr = SVR(kernel='rbf', C=grid_search.best_params_['C'], gamma=grid_search.best_params_['gamma'])
best_svr.fit(X, y)

Finalmente, se emplea el modelo entrenado para predecir los dos siguientes números primos en la secuencia:

Python
next_prime_1 = best_svr.predict(np.array(e[-2]).reshape(-1, 1))[0]
Y con esto se obtienen los mejores parámetros: {'C': 1000, 'gamma': 0.1}.

Refinamiento del modelo

Para refinar el modelo anterior y mejorar la precisión de las predicciones, se procede a ajustar los parámetros del modelo de forma más exhaustiva y utilizando técnicas de validación cruzada más avanzadas. Una opción es utilizar la búsqueda aleatoria en lugar de la búsqueda de cuadrícula para buscar los parámetros del modelo, lo que puede ser más eficiente para espacios de parámetros grandes y aleatorios como lo son estos primos.

A continuación, se muestra cómo se mejora el modelo anterior utilizando una búsqueda aleatoria con una validación cruzada de tipo k-fold (k = 10) para ajustar los parámetros del modelo y finalmente se solicita la salida de los tres posibles primos siguientes de la secuencia en la lista “e”.

Python
import numpy as np
from sklearn.model_selection import RandomizedSearchCV, KFold
from sklearn.svm import SVR

# cargar datos
e = [5,17,89,521,4253,9689,9941,11213,19937,21701,859433,1398269,2976221,3021377,6972593,32582657,43112609]
X = np.array(e[:-2]).reshape(-1, 1)
y = np.array(e[2:])

# definir espacio de parámetros a buscar
param_dist = {'C': np.logspace(-2, 10, 13),
'gamma': np.logspace(-9, 3, 13)}

# inicializar modelo y búsqueda aleatoria
svr = SVR(kernel='rbf')
cv = KFold(n_splits=10, shuffle=True, random_state=42)
random_search = RandomizedSearchCV(svr, param_distributions=param_dist, n_iter=1000, cv=cv, random_state=42, n_jobs=-1)

# ajustar modelo con búsqueda aleatoria y validación cruzada
random_search.fit(X, y)

# imprimir los mejores parámetros y el error cuadrático medio en el conjunto de prueba
print("Better parameters: ", random_search.best_params_)
print("Root mean square error in the test set: ", -random_search.best_score_)

# entrenar modelo con los mejores parámetros en todo el conjunto de datos
best_svr = SVR(kernel='rbf', C=random_search.best_params_['C'], gamma=random_search.best_params_['gamma'])
best_svr.fit(X, y)

# predecir los dos siguientes números primos en la secuencia
next_prime_1 = best_svr.predict(np.array(e[-2]).reshape(-1, 1))[0]
next_prime_2 = best_svr.predict(np.array(next_prime_1).reshape(-1, 1))[0]
next_prime_3 = best_svr.predict(np.array(next_prime_2).reshape(-1, 1))[0]

print("The next three prime numbers are: ", next_prime_1, next_prime_2, next_prime_3)

Nota: Este código utiliza una búsqueda aleatoria con una validación cruzada de tipo k-fold (k = 10) para ajustar los parámetros del modelo SVR con un kernel gaussiano. En cada iteración de la búsqueda aleatoria, se seleccionan valores aleatorios de los parámetros del modelo del espacio definido por param_dist. La búsqueda aleatoria se realiza en 1000 iteraciones y se utiliza una validación cruzada de tipo k-fold para evaluar el desempeño del modelo en cada iteración. El modelo final se entrena con los mejores parámetros encontrados en toda la secuencia de datos “e”.

Así se tiene la salida:

Better parameters: {'gamma': 2.1544346900318867e-05, 'C': 0.01},
Root mean square error in the test set: 0.0018918260689022024.
The next three prime numbers are: X_s={77075993.26585975, 93051089.6503613 and 93051137.0014563}.

3. ANÁLISIS

---

Se resalta que los datos de salida obtenidos en la aplicación del algoritmo no son 100% precisos, a saber X_1= 77075993.26585975, X_2= 93051089.6503613 y X_3=93051137.00321, pero lo que resulta interesante es que estos números presentan características fundamentales:

i) Sin decimales estos números solución X={77075993, 93051089, 93051137} son números primos.

ii) Estos tres primos pertenecen a su respectivo grupo de clasificación de Mersenne ℸ₃₁ dado que

Mod[77075993,12]=5,

Mod[93051089,12]=5,

Mod[93051137,12]=5.

Es decir; pertenecen al subgrupo seleccionado en el grupo de rotación

ℸ₃₁ Where M_ρ=31+ 31+360 K_n=2^ρ-1.

Dada estas dos características, estos tres números se establecen como altos potenciales para ser posibles primos de Mersenne. Además se resalta el hecho que después de reajustar el modelo se haya logrado obtener un error cuadrático medio en el conjunto de prueba por debajo del 2% y el modelo obtenido mediante el Kernel Gaussiano se visualiza como funcional.

4. CONCLUSIONES

---

Aplicar SVM con kernel Gaussiano a sistemas clasificados de datos establece una alternativa para la aplicación de la IA, específicamente aplicar ML, en el estudio de sistemas aleatorios de datos como lo son los primos de Mersenne posiciona una alternativa tentativa y selectiva en la búsqueda de estos números primos, previo a su largo proceso de testeo. La búsqueda aleatoria que se realizó a partir de 1000 iteraciones y con validación cruzada de tipo k-fold para evaluar el desempeño del modelo fue importante en nuestro caso.

Se recomienda como consecuencia, para diferentes prácticas y futuros trabajos de regresión o clasificación mediante algoritmos SVM, que se lleve a cabo ajustes pertinentes (como lo son el análisis de hiperparámetros, la validación cruzada y el entrenamiento respectivo) a los modelos predictivos iniciales.

Es claro que los tres números primos encontrados, al cumplir las propiedades mencionadas en el grupo de rotación Ova-angular de Mersenne, se establecen en con alto potencial para ser posibles primos de Mersenne M_ρ y por ende se invita a los grupos respectivos a efectuar un testeo de los mismos, en este artículo este es un objetivo que se escapa del interés y de las capacidades para hacerlo, los autores carecen de los recursos computaciones necesarios, pero su validación o refutación en futuros trabajos es importante y en caso de ser positivo el resultado, no solo se brindaría un nuevo número primo de Mersenne sino que se establecería una mayor articulación de la IA con el estudio de objetos matemáticos de interés.

AGRADECIMIENTOS

---

Y. Acevedo and G. Loaiza agradecen a la universidad EAFIT, Colombia, por el soporte financiero en el proyecto "Estudio de aplicaciones de procesos de difusión de importancia en salud y computación" con código 11740052022.

DECLARACIÓN DE INTERESES

---

Los autores declaran que no tienen conflicto de intereses.

REFERENCIAS