DISEÑO Y SIMULACIÓN DE ESTIMADORES DE ESTADO LINEALES Y NO LINEALES EN UN MODELO DE CONVERTIDOR DE POTENCIA DC/DC
Sergio Andrés Giraldo Ramírez1, Danny Alejandro Quiroz Pedraza2, Anderson Sebastián Torres Sánchez3, Héctor Antonio Botero Castro4
1,2,3,4Universidad Nacional de Colombia, Facultad de Minas, Departamento de Energía Eléctrica y Automática, Colombia.
1Contacto: seagiraldora@unal.edu.co
RESUMEN
La estimación de estado en convertidores electrónicos de potencia es una alternativa interesante para obtener de manera indirecta algunas variables que son difíciles de medir, debido a los costos de los sensores o a las limitaciones impuestas por los ruidos de medición. Por lo tanto, en este artículo se realiza el diseño de tres estimadores de estado lineales y tres no lineales para un modelo de convertidor boost DC/DC, con el fin de verificar la conveniencia de usar solo estimadores no lineales como solución al problema de estimación de la corriente del convertidor. Adicionalmente, se prueba mediante simulación el comportamiento de estos estimadores en el software Matlab.
Palabras clave: Estimación de estado, convertidor electrónico de potencia, filtro de Kalman, modos deslizantes, linealización.
Recibido: 4 de julio de 2022. Aceptado: 19 de septiembre de 2022
DESIGN AND SIMULATION OF LINEAR AND NONLINEAR STATE ESTIMATORS ON A MODEL OF POWER CONVERTER DC/DC
ABSTRACT
The state estimation in power electronic converters is an interesting alternative to obtain indirectly some variables that are difficult to measure, due to sensor costs or limitations imposed by measurement noise. Therefore, in this paper we design three linear and three nonlinear state estimators for a DC/DC boost converter model, in order to verify the convenience of using only nonlinear estimators as a solution to the converter current estimation problem. Additionally, the behavior of these estimators is tested by simulation in Matlab software.
Keywords: State estimation, power electronic converter, Kalman filter, sliding modes, linearization.
Received: July 4, 2022. Accepted: September 19, 2022
INTRODUCCIÓN
Los convertidores de potencia boost tienen un amplio uso en la electrónica para aumentar el voltaje de sus terminales de entrada. Para ello, se utilizan varias estrategias de control que permiten regular el voltaje de salida, independiente del efecto de la carga conectada y de las demás perturbaciones [1]. Una de las principales problemáticas que se evidencia a la hora de diseñar los controladores es la medición del voltaje y la corriente en cualquier instante de tiempo, lo cual implica el uso de sensores. Estas mediciones pueden traer complicaciones en cuanto a la implementación, especialmente para el caso de la corriente, debido a los altos costos de los sensores [2]. Debido a esto, se ha planteado como solución el diseño de estimadores de estado, los cuales cumplen la función de un sensor virtual, eliminando los problemas relacionados con la medición de corriente ([3]; [4]; [5]; [6]).
En [2] se diseña un observador de estado por modos deslizantes que impone un movimiento deslizante en las variables medidas y una dinámica asintóticamente estable en las variables no medidas. Adicionalmente, este observador permite realizar una estimación de la resistencia de carga, pero requiere la medición del voltaje de salida y de la corriente del convertidor.
En [4] se diseña un observador robusto que permite trabajar con incertidumbre en la resistencia de la carga. Este observador utiliza un modelo que tiene en cuenta varios parámetros asociados a las pérdidas eléctricas en los diferentes elementos del convertidor, como la resistencia de conducción 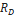 , la resistencia de conducción del diodo
, la resistencia de conducción del diodo 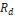 , la resistencia asociada al inductor
, la resistencia asociada al inductor 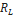 , la caída de voltaje en el diodo y los cambios en la resistencia de carga del convertidor
, la caída de voltaje en el diodo y los cambios en la resistencia de carga del convertidor 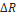 . Dicho observador utiliza la técnica de modos deslizantes para lograr la estimación robusta de la corriente.
. Dicho observador utiliza la técnica de modos deslizantes para lograr la estimación robusta de la corriente.
En [5] se diseña un observador con base en el filtro de Kalman para estimar la corriente y el voltaje de un convertidor boost, teniendo en cuenta la variación en la resistencia de carga. Para ello, los autores utilizan un módulo de eliminación de la variación de la resistencia de carga. Concretamente, se realiza la estimación de dicha resistencia con los valores del voltaje de salida y la corriente de salida estimados. Para lograr ello, se usa la ecuación de estado estacionario que relaciona la corriente del inductor con la corriente de la carga.
En [7] se diseña un observador de Luenberger no lineal para la corriente y el voltaje de un convertidor boost, cuya dinámica de error lleva asociada una matriz 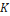 , que permite ajustar la convergencia del error a cero. La estructura del observador consiste en una copia del modelo más un factor de corrección. La desventaja de este observador es que el factor de corrección sólo afecta la dinámica del voltaje en el condensador que es la variable medida.
, que permite ajustar la convergencia del error a cero. La estructura del observador consiste en una copia del modelo más un factor de corrección. La desventaja de este observador es que el factor de corrección sólo afecta la dinámica del voltaje en el condensador que es la variable medida.
En [8] se presenta un observador de corriente robusto no lineal para convertidores con configuraciones boost, buck y buck-bost, en el cual se prueba mediante el criterio de Lyapunov la estabilidad del observador. El observador muestra un buen comportamiento ante las variaciones de la carga en los diferentes convertidores. Las pruebas se realizaron mediante simulación y análisis experimental.
En [6] se propone un observador que permite estimar la corriente por el inductor del convertidor boost, con base en la medición del voltaje de salida, pero sin considerar la medición del voltaje de la fuente. Esto es lo que se llama un observador de entradas desconocidas. El diseño del estimador de estado se basa en el método de inmersión – invarianza en el cual hay cuatro pasos que se deben seguir [9]. Primero, se debe asignar una dinámica objetivo que evoluciona a lo largo de un espacio de estado separado, el cual es generalmente de dimensión menor que la del estado original. Segundo, se debe proponer un mapeo suave, llamado mapeo de inmersión, el cual mapea el espacio de estado objetivo a una sub-variedad del espacio de estado original. Tercero, se debe encontrar una ley de control que hace que esta sub-variedad sea invariante y que su dinámica sea la imagen de la dinámica objetivo a través de la inmersión. Finalmente, se debe garantizar que la ley de control haga que esta sub-variedad sea globalmente atractiva, mientras se mantienen todos los estados delimitados.
Como puede observarse esta es un área de trabajo muy importante en la electrónica de potencia, pero que muchos investigadores no conocen. En este sentido, este trabajo busca acercar a la comprensión del diseño de los observadores de estado para convertidores DC/DC y su análisis mediante simulación. El objetivo central del documento es mostrar las limitaciones que se tienen cuando se diseñan observadores lineales clásicos, ya que se produce error de estado estacionario en la estimación. Por lo tanto, se mejoran los diseños lineales con las versiones no lineales de los mismos. Los resultados se analizan mediante simulación. El documento está organizado de la siguiente forma: en la Sección 2 se aborda la descripción del funcionamiento del convertidor boost y el modelado de este. En la Sección 3 se obtiene una representación lineal del modelo del convertidor y se analizan las limitaciones de dicha linealización. En la Sección 4 se realiza el diseño de tres observadores de estado lineales (observador de Luenberger, filtro de Kalman, observador por modos deslizantes) y se comparan los resultados obtenidos con los mismos tres observadores pero en versiones no lineales. Las comparaciones se realizan mediante simulaciones realizadas en el software Matlab. Finalmente, en la Sección 5 se describen las conclusiones del trabajo.
MODELO DEL CONVERTIDOR
En la Figura 1 se observa el circuito equivalente del convertidor boost con los elementos de conmutación necesarios. Este se compone de un interruptor conmutado de dos posiciones 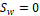 y
y 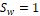 . De manera práctica, este interruptor es implementado por un diodo y un transistor, donde el transistor funciona en la región de corte–saturación actuando como un interruptor de una posición, es decir, completamente abierto o cerrado. Para el caso del diodo, no es necesario controlarlo, ya que ambos actúan de forma independiente. Por lo tanto, cuando conduce el diodo, el transistor no lo hace y viceversa, esto siempre y cuando no se opere en modo discontinuo, donde puede darse el caso en que ambos elementos operen al mismo tiempo. Para saber la dirección del ánodo y del cátodo del diodo se realiza un análisis de direcciones de las corrientes en el convertidor. Esta técnica es conocida como switch realization [10].
. De manera práctica, este interruptor es implementado por un diodo y un transistor, donde el transistor funciona en la región de corte–saturación actuando como un interruptor de una posición, es decir, completamente abierto o cerrado. Para el caso del diodo, no es necesario controlarlo, ya que ambos actúan de forma independiente. Por lo tanto, cuando conduce el diodo, el transistor no lo hace y viceversa, esto siempre y cuando no se opere en modo discontinuo, donde puede darse el caso en que ambos elementos operen al mismo tiempo. Para saber la dirección del ánodo y del cátodo del diodo se realiza un análisis de direcciones de las corrientes en el convertidor. Esta técnica es conocida como switch realization [10].
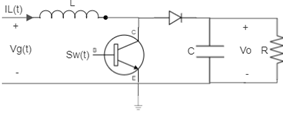
Figura 1. Circuito de un convertidor boost con diodo y transistor.
El convertidor de potencia boost DC/DC al ser un sistema conmutado genera cambios en la dinámica del sistema, dependiendo de la posición del interruptor. Por lo tanto, el modelo completo del convertidor incluye una variable relacionada con la apertura o cierre del interruptor que es idealmente una función a tramos de dos valores constantes: cero y uno. Debido a que en este caso el interés es conocer los valores medios de las variables de estado del convertidor de potencia, se realiza una simplificación al modelo y se utiliza un modelo promediado. Cabe recalcar que este modelo promediado se usa especialmente en la representación en el espacio de estados para el análisis dinámico. Para el diseño del convertidor, es decir, para encontrar los valores de la inductancia, la capacitancia, el tipo de transistor, entre otros, se requiere conocer cómo es la variación de la dinámica de las variables de estado respecto a su valor medio, conocida como rizado [10].
En la literatura existen otros tipos de métodos de modelado para los convertidores o circuitos conmutados, por ejemplo el modelo de estado híbrido [2]. Este modelo es más preciso que el modelo promediado, además, cuando los rizados son muy grandes el modelo promediado no es válido ya que tiene que cumplir algunas restricciones sobre el porcentaje de rizado de las variables [10]
El modelado del convertidor boost mostrado en la Figura 1, y de cualquier convertidor en general, se realiza obteniendo las ecuaciones diferenciales que definen la dinámica de los valores medios de las variables de estado del sistema asociadas a los elementos almacenadores de energía, es decir los capacitores e inductores. Una hipótesis de modelado para el sistema de la Figura 1 se ilustra en la Figura 2, donde el transistor y el diodo son reemplazados por un suiche.
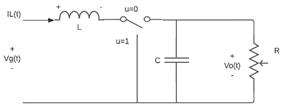
Figura 2. Hipótesis de modelado del circuito de un convertidor boost.
Así, haciendo uso de las leyes de Kirchhoff y la ley de Ohm (conservación de la energía), se obtienen las ecuaciones que rigen el sistema en función de 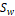 . Si
. Si 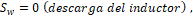 se tienen dos ecuaciones diferenciales (una para cada variable de estado) que describen la dinámica del convertidor bajo esa condición. Por otro lado, si
se tienen dos ecuaciones diferenciales (una para cada variable de estado) que describen la dinámica del convertidor bajo esa condición. Por otro lado, si 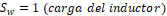 se tiene un sistema de ecuaciones diferenciales diferente al anterior. El modelo que representa estas dos situaciones viene dado por:
se tiene un sistema de ecuaciones diferenciales diferente al anterior. El modelo que representa estas dos situaciones viene dado por:
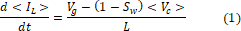
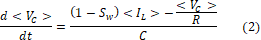
Donde 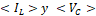 son los valores medios de la corriente en el inductor y el voltaje en el capacitor respectivamente,
son los valores medios de la corriente en el inductor y el voltaje en el capacitor respectivamente, 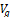 es el voltaje de entrada del convertidor y R, L, C son los parámetros del circuito de la Figura 2. En este trabajo se requiere un modelo explicativo del convertidor con el fin de diseñar observadores de estado que permitan estimar la corriente del convertidor con base en la medición del voltaje en el capacitor. Por lo tanto, no es deseable tener un modelo con una variable discontinua como lo es
es el voltaje de entrada del convertidor y R, L, C son los parámetros del circuito de la Figura 2. En este trabajo se requiere un modelo explicativo del convertidor con el fin de diseñar observadores de estado que permitan estimar la corriente del convertidor con base en la medición del voltaje en el capacitor. Por lo tanto, no es deseable tener un modelo con una variable discontinua como lo es 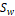 . Debido a esto, se calcula el valor promedio de
. Debido a esto, se calcula el valor promedio de 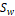 que permita representar de manera adecuada la dinámica del convertidor boost y garantizar la observabilidad en el modelo. Para ello, se resalta que la variable
que permita representar de manera adecuada la dinámica del convertidor boost y garantizar la observabilidad en el modelo. Para ello, se resalta que la variable 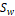 toma un valor de 1 durante un intervalo
toma un valor de 1 durante un intervalo 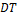 y cero durante un intervalo
y cero durante un intervalo 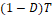 , siendo D la relación entre el tiempo en que el interruptor está en la posición
, siendo D la relación entre el tiempo en que el interruptor está en la posición 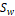 = 0 y el tiempo en que el interruptor está en la posición
= 0 y el tiempo en que el interruptor está en la posición 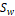 = 1. Esta relación es conocida como ciclo de trabajo y T es el periodo de conmutación, es decir, el tiempo total en el que se realiza el proceso de apertura y cierre del interruptor. Para aclarar esto, en la Figura 3 se muestra la variable
= 1. Esta relación es conocida como ciclo de trabajo y T es el periodo de conmutación, es decir, el tiempo total en el que se realiza el proceso de apertura y cierre del interruptor. Para aclarar esto, en la Figura 3 se muestra la variable 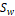 en el tiempo con cada uno de los parámetros mencionados.
en el tiempo con cada uno de los parámetros mencionados.
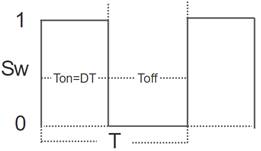
Figura 3. Comportamiento de la variable 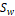
Si se calcula el valor promedio de la señal 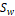 en el periodo de tiempo T se obtiene:
en el periodo de tiempo T se obtiene:
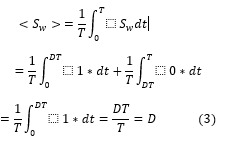
Reemplazando (3) en (1) y (2) se obtiene el modelo promediado para el sistema convertidor boost DC/DC descrito por las ecuaciones (4) y (5).
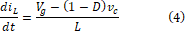
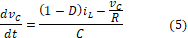
Para que este modelo sea válido se deben cumplir las siguientes suposiciones:
- El periodo de conmutación es T y el interruptor está cerrado un tiempo
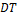 y abierto el resto del tiempo
y abierto el resto del tiempo 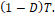
- La corriente en la bobina es permanente (siempre positiva).
- Memoria RAM de 3 Gb.
- Los componentes R, L y C son ideales.
- El valor medio de las variables de estado es mayor que su rizado.
Se observa de las ecuaciones (4) y (5) que el sistema tiene como entradas 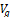 y D, por lo tanto se definen los vectores de estado y entradas como:
y D, por lo tanto se definen los vectores de estado y entradas como:
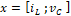 ,
,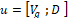
Y el modelo toma la forma 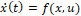 . Además, se evidencia que el sistema convertidor boost DC/DC es continuo y bilineal, debido a que hay multiplicación entre variables de estado y entradas.
. Además, se evidencia que el sistema convertidor boost DC/DC es continuo y bilineal, debido a que hay multiplicación entre variables de estado y entradas.
LINEALIZACIÓN DEL MODELO Y SUS LIMITACIONES
Debido a que el sistema descrito en (4) y (5) es bilineal y conociendo que el propósito inicial de este artículo es diseñar observadores lineales, se procede a linealizar el modelo alrededor de un punto de operación para obtener una representación en espacio de estados lineal de la forma:
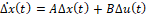 (6)
(6)
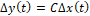 (7)
(7)
Donde las matrices A, B y C se obtienen como los jacobianos de linealización de la forma:
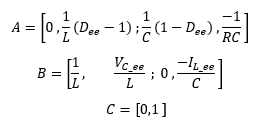 (8)
(8)
Por nomenclatura, en las matrices las comas separan elementos y los punto y coma separan las filas. Donde 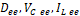 , son las variables del sistema evaluadas en el punto de operación, y se considera la matriz C de forma que la salida medida es el voltaje del capacitor, es decir el voltaje en la carga.
, son las variables del sistema evaluadas en el punto de operación, y se considera la matriz C de forma que la salida medida es el voltaje del capacitor, es decir el voltaje en la carga.
Punto de equilibrio del modelo
El punto de equilibrio se puede determinar igualando a cero los lados izquierdos de las ecuaciones (4) y (5) y despejando las variables de estado. Dicho punto estará determinado por los valores de estado estacionario seleccionados para las entradas (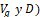 , de forma que:
, de forma que:
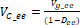 (9)
(9)
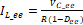 (10)
(10)
Esta última ecuación se puede mostrar como:
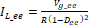 (11)
(11)
Las cuales dependen únicamente de los valores de estado estacionario en las entradas. Para los diseños que se van a realizar aquí, se seleccionan los valores para los parámetros y el punto de operación que se muestran en las Tablas 1 y 2.
Tabla 1. Parámetros del convertidor, tomados de [5]
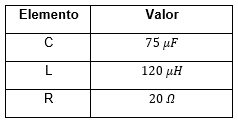
Tabla 2. Variables del convertidor para el punto de equilibrio, tomados de [5]
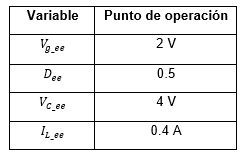
Con los valores anteriores, las matrices del modelo lineal en el espacio de estado son:
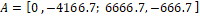
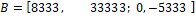
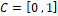
Analizando la estabilidad del sistema linealizado, se comprueba que la ubicación de los polos es 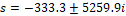 , por lo tanto, al tener parte real negativa y estar ubicados en el semiplano izquierdo, el punto de operación es estable. Obtenido el modelo lineal, se debe verificar que este represente adecuadamente el modelo no lineal cerca del punto de operación. Por lo tanto, se realiza una simulación de ambos sistemas alrededor de este punto, introduciendo una perturbación que consiste en un incremento del 10% en el voltaje de entrada en 0.02 s, seguido de un incremento del 10% en el ciclo de trabajo en 0.04 s. Los resultados se pueden observar en las Figuras 4.a y 4.b.
, por lo tanto, al tener parte real negativa y estar ubicados en el semiplano izquierdo, el punto de operación es estable. Obtenido el modelo lineal, se debe verificar que este represente adecuadamente el modelo no lineal cerca del punto de operación. Por lo tanto, se realiza una simulación de ambos sistemas alrededor de este punto, introduciendo una perturbación que consiste en un incremento del 10% en el voltaje de entrada en 0.02 s, seguido de un incremento del 10% en el ciclo de trabajo en 0.04 s. Los resultados se pueden observar en las Figuras 4.a y 4.b.
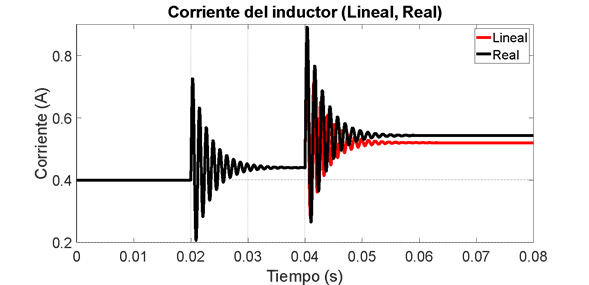
Figura 4.a. Modelo lineal vs modelo no lineal. Corriente del inductor.
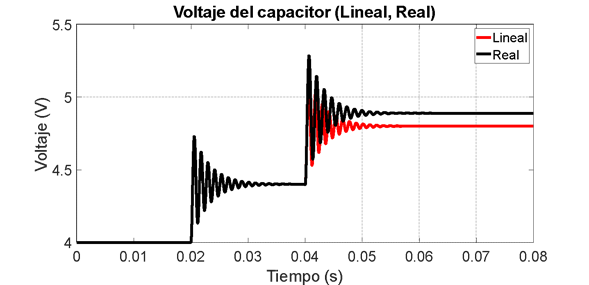
Figura 4.b. Modelo lineal vs modelo no lineal. Voltaje del capacitor.
En la Figura 4.a se observa que para la corriente del inductor el sistema lineal representa con gran precisión al modelo no lineal. Sin embargo, ante el cambio en el ciclo de trabajo, se aprecia que al final aparece un error de estado estacionario. Para el caso del voltaje en el capacitor se observa un comportamiento similar al anteriormente mencionado, lo cual se evidencia en la figura 4.b. Analizando más a fondo el error de estado estacionario, entre más cercano se encuentre el valor del ciclo de trabajo 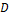 al valor de 1, mayor es el desacople entre las dos mallas del circuito. Este es el valor promedio de la entrada real del convertidor dada por la posición del interruptor (
al valor de 1, mayor es el desacople entre las dos mallas del circuito. Este es el valor promedio de la entrada real del convertidor dada por la posición del interruptor (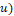 , la cual al ser igual a 1 representa un desacople total de los elementos almacenadores de energía que componen el sistema. Para comprobar lo anterior, se realiza nuevamente la comparación entre el modelo lineal y el no lineal, esta vez tomando como punto de operación
, la cual al ser igual a 1 representa un desacople total de los elementos almacenadores de energía que componen el sistema. Para comprobar lo anterior, se realiza nuevamente la comparación entre el modelo lineal y el no lineal, esta vez tomando como punto de operación 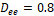 , y realizando un incremento del 10% en
, y realizando un incremento del 10% en 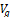 en t= 0.02 s seguido por un incremento del 10% en D en t=0.04 s, tal y como se observa en las Figuras 5.a. y 5.b.
en t= 0.02 s seguido por un incremento del 10% en D en t=0.04 s, tal y como se observa en las Figuras 5.a. y 5.b.
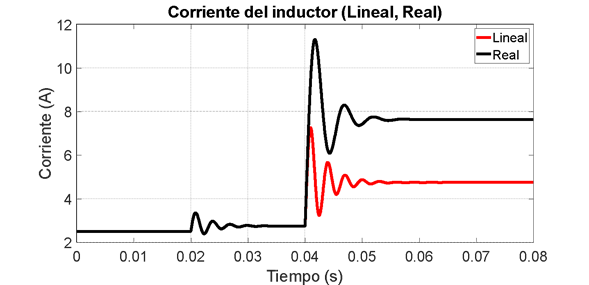
Figura 5.a. Modelo lineal vs modelo no lineal. Corriente del inductor.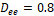
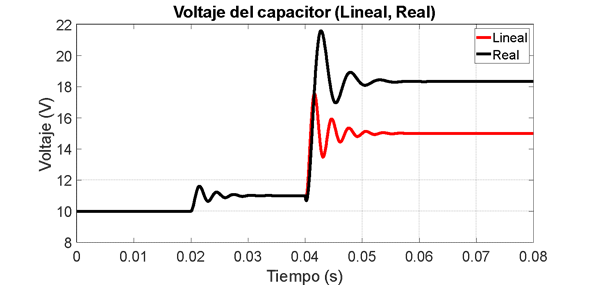
Figura 5.b. Modelo lineal vs modelo no lineal. Voltaje del capacitor.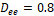
De acuerdo con lo anterior, se puede observar que al estar más cerca de una situación de desacople de las mallas, el modelo lineal difiere en mayor medida del modelo no lineal ante variaciones en el ciclo de trabajo, evidenciando un gran error de estado estacionario. Para analizar matemáticamente esto, se calculan las ecuaciones que muestran la ganancia de estado estacionario en el modelo lineal para cada una de los cambios en las entradas, las cuales vienen dadas, para el caso de la entrada 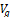 , por:
, por:
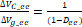 (12)
(12)
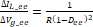 (13)
(13)
Estas dos ecuaciones son iguales a las correspondientes del modelo no lineal (9) y (11). Por lo tanto, la ganancia de estado estacionario para el cambio en 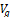 es la misma en el caso lineal y en el no lineal. Esto permite concluir que el modelo linealizado no tendrá problemas de estado estacionario ante esta entrada, lo cual se evidenció también en las Figuras 4a, 4b, 5a y 5b.
es la misma en el caso lineal y en el no lineal. Esto permite concluir que el modelo linealizado no tendrá problemas de estado estacionario ante esta entrada, lo cual se evidenció también en las Figuras 4a, 4b, 5a y 5b.
De otro lado, para el cambio en D se obtienen las siguientes ganancias de estado estacionario del modelo linealizado:

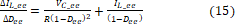
Estas ganancias dependen de las condiciones de operación, es decir del voltaje en el condensador y de la corriente por la bobina, esto hará que el modelo lineal tenga problemas de estado estacionario ante esta entrada, lo cual se evidenció también en las Figuras 4a, 4b, 5a y 5b.
Una vez comprobadas algunas propiedades importantes del modelo lineal, es posible diseñar observadores de estado usando técnicas lineales, pero entendiendo el problema que va a existir con el estado estacionario cuando cambie el ciclo de trabajo D. Por lo tanto, también se deben diseñar las versiones no lineales de dichos estimadores. En la siguiente sección se explica todo esto de manera detallada.
DISEÑO Y SIMULACIÓN DE OBSERVADORES
1.Diseño y simulación de observadores lineales
A continuación, se diseñan observadores lineales de estado para el convertidor boost DC/DC, los cuales pueden servir para el control, la detección de fallas o el monitoreo. Inicialmente se verifica la observabilidad del modelo, para luego diseñar los observadores.
Observabilidad lineal del modelo
Para el sistema lineal, se puede analizar la observabilidad, suponiendo un punto de operación. La observabilidad define si existen o no estados iniciales indistinguibles alrededor de ese punto, lo cual se puede verificar mediante una prueba de rango de matriz [11]. Dicha matriz se obtiene desde el modelo linealizado así:
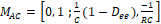
Se observa de la matriz anterior que el sistema será observable, ya que el rango de la matriz 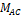 será igual a 2, siempre y cuando el valor de
será igual a 2, siempre y cuando el valor de 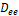 sea diferente de 1. Lo anterior quiere decir que cuando
sea diferente de 1. Lo anterior quiere decir que cuando 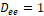 existen estados iniciales indistinguibles y no es posible determinar de manera unívoca el estado desde la salida. Esto ocurre cuando el suiche de la Figura 2 se encuentra en la posición 1 de manera permanente, y en ese caso las dos mallas del circuito se encuentran desacopladas. En esta situación pueden existir condiciones iniciales diferentes en la corriente la bobina y el voltaje del capacitor que generan la misma salida, es decir estados iniciales indistinguibles y por lo tanto la pérdida de la observabilidad. Desde el punto de vista práctico, esta situación implica una saturación permanente en el actuador (que en este caso es el transistor de potencia). Sin embargo, debido a que la principal característica de un convertidor es que es un circuito de conmutación, no tiene sentido que D sea 1 de forma permanente, ya que esto implicaría que no hay conmutación. Por lo tanto, se concluye que el sistema lineal es localmente observable. Una situación similar se puede verificar en el caso que la salida sea la corriente por el inductor.
existen estados iniciales indistinguibles y no es posible determinar de manera unívoca el estado desde la salida. Esto ocurre cuando el suiche de la Figura 2 se encuentra en la posición 1 de manera permanente, y en ese caso las dos mallas del circuito se encuentran desacopladas. En esta situación pueden existir condiciones iniciales diferentes en la corriente la bobina y el voltaje del capacitor que generan la misma salida, es decir estados iniciales indistinguibles y por lo tanto la pérdida de la observabilidad. Desde el punto de vista práctico, esta situación implica una saturación permanente en el actuador (que en este caso es el transistor de potencia). Sin embargo, debido a que la principal característica de un convertidor es que es un circuito de conmutación, no tiene sentido que D sea 1 de forma permanente, ya que esto implicaría que no hay conmutación. Por lo tanto, se concluye que el sistema lineal es localmente observable. Una situación similar se puede verificar en el caso que la salida sea la corriente por el inductor.
Observador de Luenberger lineal
El observador de Luenberger se basa en el mismo modelo de la planta para determinar el comportamiento de las variables de estado a partir de las entradas y salidas del sistema. Además, se incluye un factor de corrección que permite mejorar el comportamiento del observador y lograr la estabilidad en este, independientemente de la dinámica de la planta. El modelo del observador de Luenberger en lazo cerrado se muestra a continuación [11]:
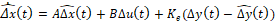 (16)
(16)
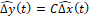 (17)
(17)
La dinámica de este observador se puede modificar manipulando la matriz de ganancias 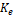 , si el sistema es observable. Sin embargo, debido a que este estimador no es robusto ante el ruido que se puede introducir en la medición
, si el sistema es observable. Sin embargo, debido a que este estimador no es robusto ante el ruido que se puede introducir en la medición 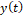 , entre mayor sea la ganancia del estimador habrá una mayor amplificación de este, degradando el estado estimado. Para el presente diseño
, entre mayor sea la ganancia del estimador habrá una mayor amplificación de este, degradando el estado estimado. Para el presente diseño 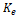 se calculó mediante la fórmula de Ackermann, de forma que los dos polos del observador estuvieran ubicados en -5270, que corresponde a la magnitud de los polos del sistema linealizado, con lo cual se obtuvo
se calculó mediante la fórmula de Ackermann, de forma que los dos polos del observador estuvieran ubicados en -5270, que corresponde a la magnitud de los polos del sistema linealizado, con lo cual se obtuvo 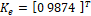 . Para la simulación del observador, las condiciones iniciales del convertidor son diferentes a las del observador. Para el voltaje en el capacitor las condiciones iniciales son de
. Para la simulación del observador, las condiciones iniciales del convertidor son diferentes a las del observador. Para el voltaje en el capacitor las condiciones iniciales son de 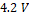 para el voltaje estimado y
para el voltaje estimado y 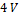 para el voltaje real; y para la corriente en el inductor las condiciones iniciales son de
para el voltaje real; y para la corriente en el inductor las condiciones iniciales son de 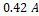 para la estimada y
para la estimada y 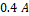 para la real. Además, se introduce un aumento en las entradas
para la real. Además, se introduce un aumento en las entradas 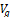 y
y 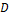 del 5% a los
del 5% a los 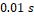 y
y 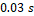 respectivamente, es decir
respectivamente, es decir 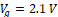 y
y 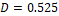 . En las Figuras 6 y 7 se observan las variables de estado reales y estimadas del convertidor boost asumiendo que existe ruido de medición en
. En las Figuras 6 y 7 se observan las variables de estado reales y estimadas del convertidor boost asumiendo que existe ruido de medición en 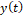 . Se evidencia una convergencia asintótica de las variables de estado del observador en un tiempo impuesto por el vector de ganancias
. Se evidencia una convergencia asintótica de las variables de estado del observador en un tiempo impuesto por el vector de ganancias 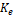 .
.
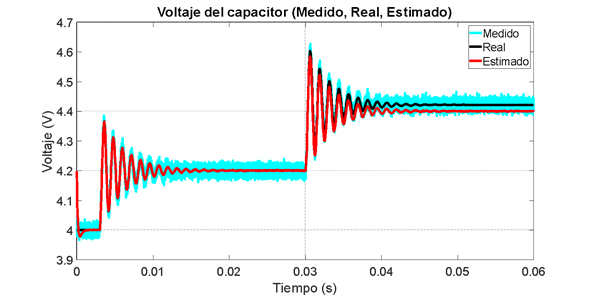
Figura 6. Estimación de Voltaje. Observador de Luenberger.
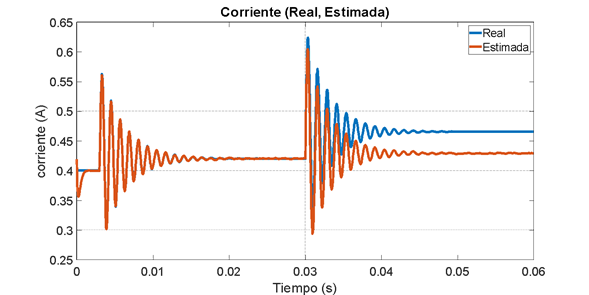
Figura 7. Estimación de corriente. Observador de Luenberger.
De acuerdo con los resultados obtenidos en las simulaciones, se observa que se tiene una correcta estimación de la corriente, la cual no es medida. Sin embargo, se observa que se presenta un error de estado estacionario después de 0.045 s debido a que el sistema ya no se encuentra en cercanías del punto de operación. Eso debido a que el sistema linealizado utilizado para el desarrollo del observador difiere con el sistema real, generando una pequeña desviación en los valores estimados de la corriente del inductor.
Filtro de Kalman lineal
Partiendo del modelo lineal, se diseñó un filtro de Kalman para realizar la estimación de los estados. El modelo de este estimador se elabora teniendo en cuenta un algoritmo que consta de tres etapas correspondientes a las condiciones iniciales con las cuales se comienza el proceso de estimación, para continuar con la predicción y la corrección [12]. Gracias a que este estimador considera los ruidos de proceso y medición, es robusto ante estos, y a su vez, realiza un filtrado de la señal. Sin embargo, como se podrá observar en el algoritmo que sigue, no es posible modificar su dinámica mediante una ubicación de polos como en el observador de Luenberger. Cada una de las etapas del algoritmo se describe a continuación.
Inicio:
- Condiciones iniciales:
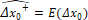 (18)
(18)
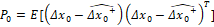 (19)
(19)
Proceso recursivo:
- Predicción:
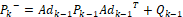 (20)
(20)
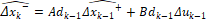 (21)
(21)
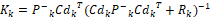 (22)
(22)
- Corrección:
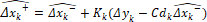 (23)
(23)
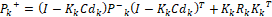 (24)
(24)
Donde P corresponde a una matriz que contiene las covarianzas del ruido del proceso y de medición, 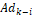 ,
, 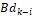 y
y 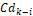 son las matrices en el espacio de estado discreto del modelo lineal, y Q y R son las matrices que contienen las varianzas del ruido del proceso y de medición respectivamente y E es el operador esperanza matemática. En este caso Q=diag(0.001^2) y R=0.01^2 debido a que se quiere evaluar la capacidad del estimador para filtrar el ruido del sistema. Las variables denotadas con el superíndice (–) corresponden a variables a priori, mientras que las que están denotadas con superíndice (+) son variables a posteriori. El tiempo de discretización es de
son las matrices en el espacio de estado discreto del modelo lineal, y Q y R son las matrices que contienen las varianzas del ruido del proceso y de medición respectivamente y E es el operador esperanza matemática. En este caso Q=diag(0.001^2) y R=0.01^2 debido a que se quiere evaluar la capacidad del estimador para filtrar el ruido del sistema. Las variables denotadas con el superíndice (–) corresponden a variables a priori, mientras que las que están denotadas con superíndice (+) son variables a posteriori. El tiempo de discretización es de 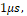 de forma que sea lo suficientemente menor a la constante de tiempo del sistema,
de forma que sea lo suficientemente menor a la constante de tiempo del sistema, 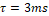 >, impuesta por los polos, y así tener una correcta representación del sistema discreto.
>, impuesta por los polos, y así tener una correcta representación del sistema discreto.
A continuación se muestran las simulaciones realizadas para la estimación de la corriente a partir de la medición del voltaje. Para las simulaciones, el estado del sistema comienza en el punto de operación, mientras que el filtro de Kalman comienza un 10% alejado de las condiciones iniciales. A su vez, la matriz inicial P es igual a la matriz de ruido de covarianza del proceso Q, debido a que aún no se tienen mediciones disponibles en t=0. En toda la simulación se tuvo un ruido de proceso con desviación de 0.001 y un ruido de medición con media cero y desviación de 0.01. Los cambios en las entradas son los mismos del caso anterior. Los resultados se pueden observar en las Figuras 8 y 9.
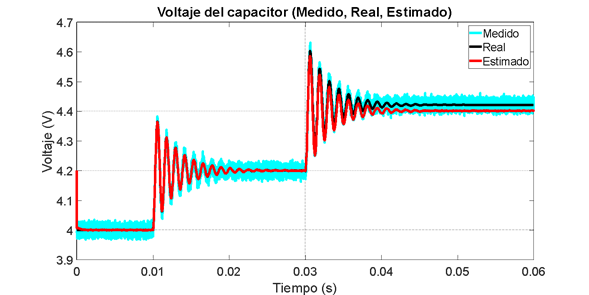
Figura 8. Estimación de voltaje con ruido. Filtro de Kalman
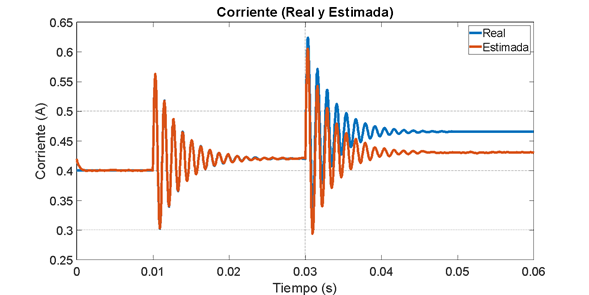
Figura 9. Estimación de corriente con ruido. Filtro de Kalman
Al observar la variable medida en la Figura 8, se puede apreciar la robustez del estimador ante el ruido, el cual se logra filtrar exitosamente. Adicionalmente se puede ver como el estado estimado sigue adecuadamente el medido. Sin embargo, al realizar una perturbación en la entrada D en 0.03 s, el estimador presenta un pequeño error de estado estacionario debido a que está trabajando lejos del punto de operación. Finalmente se realiza la estimación de la corriente a partir de la medición del voltaje. En la Figura 9 se observa que el estimador de corriente funciona adecuadamente, y al igual que en el caso anterior, hay un error en estado estacionario luego de 0.045 s.
Observador por modos deslizantes lineal
Para el diseño del observador por modos deslizantes se utiliza una transformación lineal de variables de estado, que consiste en separar el estado medible y el no medible [13]. Esta separación consiste en obtener las dinámicas de forma independiente para la parte medible y para la no medible del estado, que se van a denominar 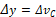 y
y 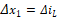 respectivamente. En este caso las ecuaciones (5) y (4) corresponden a este requerimiento. Por lo tanto, el sistema linealizado se puede mostrar como:
respectivamente. En este caso las ecuaciones (5) y (4) corresponden a este requerimiento. Por lo tanto, el sistema linealizado se puede mostrar como:
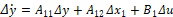 (25)
(25)
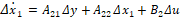 (26)
(26)
El observador por modos deslizantes para cada una de las partes mencionadas tiene la siguiente estructura [13]:
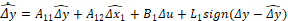 (27)
(27)
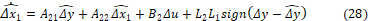
Donde 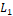 es una matriz (m x n) con m el número de salidas medibles, en este caso solo se medirá el voltaje en el capacitor
es una matriz (m x n) con m el número de salidas medibles, en este caso solo se medirá el voltaje en el capacitor 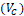 , por lo tanto la dimensión de
, por lo tanto la dimensión de 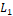 es (1 x 1). Para
es (1 x 1). Para 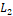 se tiene que es una matriz de dimensiones (n-m)*m. Debido a que el convertidor boost tiene dos variables de estado
se tiene que es una matriz de dimensiones (n-m)*m. Debido a que el convertidor boost tiene dos variables de estado 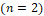 , la dimensión de la matriz
, la dimensión de la matriz 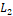 es (1 x 1). Además, se tiene que la dinámica del error de estimación en la medición
es (1 x 1). Además, se tiene que la dinámica del error de estimación en la medición 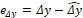 viene dada por:
viene dada por:
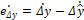 (29)
(29)
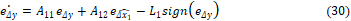
La selección de 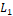 se realiza por medio de ensayo–acierto, tal que se logre la convergencia en tiempo finito del error en la parte medible del convertidor boost hacia la superficie deslizante
se realiza por medio de ensayo–acierto, tal que se logre la convergencia en tiempo finito del error en la parte medible del convertidor boost hacia la superficie deslizante 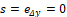 , y luego hacia el origen. A través de ensayo-acierto se seleccionó la ganancia L1=100. Respecto a la parte no medible (estimada) se tiene para la dinámica del error lo siguiente:
, y luego hacia el origen. A través de ensayo-acierto se seleccionó la ganancia L1=100. Respecto a la parte no medible (estimada) se tiene para la dinámica del error lo siguiente:
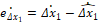 (31)
(31)
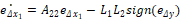 (32)
(32)
Si se aplica el concepto de control equivalente [13], se obtiene la dinámica del error de la parte no medible así:
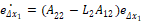 (33)
(33)
Donde el cálculo de la matriz de ganancia 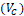 se realiza de forma análoga a un observador de Luenberger, es decir, se impone la dinámica del error por medio de un polinomio deseado que determina los polos del observador, logrando la convergencia deseada para
se realiza de forma análoga a un observador de Luenberger, es decir, se impone la dinámica del error por medio de un polinomio deseado que determina los polos del observador, logrando la convergencia deseada para 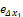 siempre y cuando el par (
siempre y cuando el par (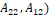 sea observable. En este caso, el valor de L2 se seleccionó de forma que la dinámica para el error en la estimación de la corriente tuviera un tiempo de convergencia de
sea observable. En este caso, el valor de L2 se seleccionó de forma que la dinámica para el error en la estimación de la corriente tuviera un tiempo de convergencia de 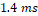 . El valor de la ganancia L2 que determina el criterio establecido es L2=1 que origina un polo en
. El valor de la ganancia L2 que determina el criterio establecido es L2=1 que origina un polo en 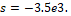 Para la simulación de este observador se introducen las mismas perturbaciones del caso anterior. Los resultados se evidencian en las Figuras 10 y 11. En ambas figuras se observa un error en el transitorio y en el estado estacionario de la corriente, producto de la utilización del modelo linealizado alrededor del punto de operación para el diseño del observador lineal.
Para la simulación de este observador se introducen las mismas perturbaciones del caso anterior. Los resultados se evidencian en las Figuras 10 y 11. En ambas figuras se observa un error en el transitorio y en el estado estacionario de la corriente, producto de la utilización del modelo linealizado alrededor del punto de operación para el diseño del observador lineal.
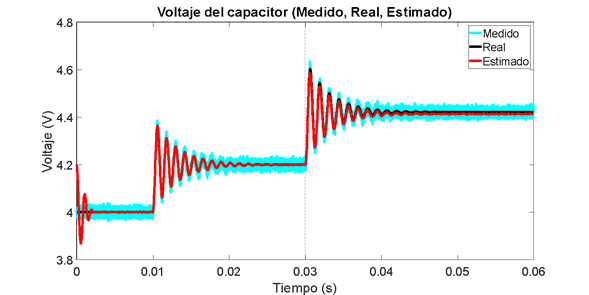
Figura 10. Estimación del voltaje. Observador por modos deslizantes
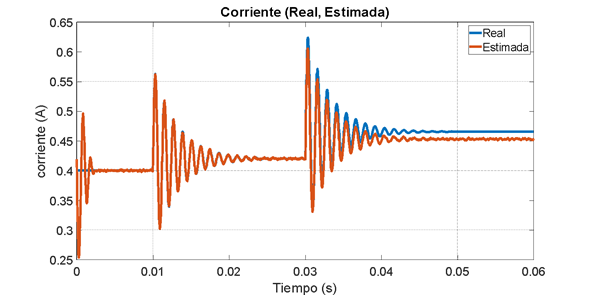
Figura 11. Estimación de la corriente. Observador por modos deslizantes
En la Figura 10 puede verse la convergencia en tiempo finito del voltaje del capacitor en 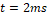 , lo cual se amplifica en la Figura 12. Así mismo, en la Figura 11 se puede observar la respuesta asintótica de la corriente con un tiempo de establecimiento aproximado de
, lo cual se amplifica en la Figura 12. Así mismo, en la Figura 11 se puede observar la respuesta asintótica de la corriente con un tiempo de establecimiento aproximado de 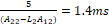 .
.
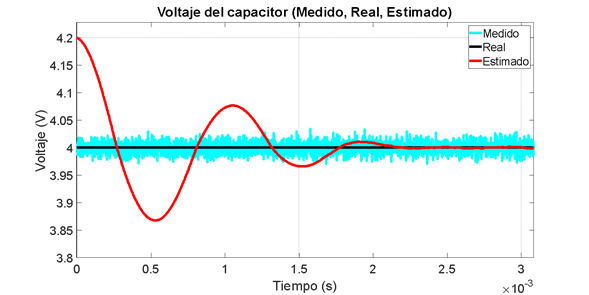
Figura 12. Convergencia en tiempo finito. Observador por modos deslizantes
2. Diseño y simulación de observadores no lineales
Debido a la problemática de error de estado estacionario que se explicó en la sección anterior, a continuación se diseñan observadores no lineales de estado para el convertidor boost DC/DC. Sin embargo, primero se debe verificar la observabilidad no lineal para proceder al diseño de los observadores.
Observabilidad no lineal del modelo
La condición para que un sistema no lineal posea observabilidad, es que la dimensión de la distribución de observabilidad sea igual a la dimensión del espacio de estado [11]. En [14] se muestra un análisis de la observabilidad de un convertidor boost ideal y uno no ideal usando el álgebra de Lie, pero sin considerar el ciclo de dureza 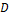 en el análisis. En este trabajo se considerará la observabilidad no lineal teniendo en cuenta el ciclo de dureza
en el análisis. En este trabajo se considerará la observabilidad no lineal teniendo en cuenta el ciclo de dureza 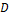 . Para ello se calcula el espacio de observación como:
. Para ello se calcula el espacio de observación como:

Donde 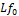 y
y 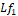 son las derivadas de Lie definidas como:
son las derivadas de Lie definidas como:


Procediendo se obtiene:

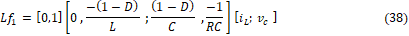
De donde el espacio de observación es:
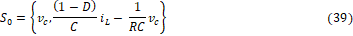
Por lo tanto, la distribución de observabilidad viene dada por:
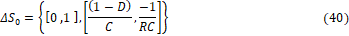
La matriz de observabilidad es:
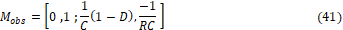
El rango de la matriz 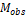 es igual 2, es decir la dimensión del sistema, si el ciclo de dureza
es igual 2, es decir la dimensión del sistema, si el ciclo de dureza 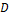 es diferente de uno. Dicha observabilidad se pierde cuando
es diferente de uno. Dicha observabilidad se pierde cuando 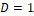 porque el suiche en esta posición produce dos mallas desacopladas (
porque el suiche en esta posición produce dos mallas desacopladas (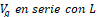 y
y 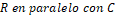 ), en las cuales pueden existir condiciones iniciales diferentes que producen la misma salida en
), en las cuales pueden existir condiciones iniciales diferentes que producen la misma salida en 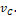 Es decir, en esta condición hay estados iniciales indistinguibles y por lo tanto no es posible reconstruir el estado de manera unívoca. Sin embargo, esta condición de operación solo ocurre cuando hay una saturación en el actuador, lo cual se debería prevenir en el caso real.
Es decir, en esta condición hay estados iniciales indistinguibles y por lo tanto no es posible reconstruir el estado de manera unívoca. Sin embargo, esta condición de operación solo ocurre cuando hay una saturación en el actuador, lo cual se debería prevenir en el caso real.
Observador de Luenberger no lineal
El observador de Luenberger no lineal, al igual que el lineal, se basa en el modelo no lineal de la planta e incluye un factor de corrección que permite mejorar el comportamiento del observador y lograr la estabilidad en este, independientemente de la dinámica de la planta. El modelo del observador de Luenberger no lineal en lazo cerrado se muestra a continuación [11]:
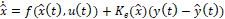 (42)
(42)
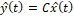 (43)
(43)
Note que en este caso el observador trabaja con el modelo no lineal de la planta. La dinámica de este observador también se puede modificar manipulando la matriz de ganancias 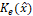 , si el sistema es observable. Como ya está garantizada la observabilidad no lineal, para el presente diseño
, si el sistema es observable. Como ya está garantizada la observabilidad no lineal, para el presente diseño 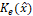 se calculó mediante la fórmula de Ackermann, pero aquí se debe hacer de forma recursiva porque depende del estado estimado. Para ello, se buscó que los dos polos del observador estuvieran ubicados en -5270, que corresponde a la magnitud de los polos del sistema linealizado. Las condiciones de simulación son las mismas del caso lineal. En las Figuras 13 y 14 se observan las variables de estado reales y estimadas del convertidor boost asumiendo que existe ruido de medición en
se calculó mediante la fórmula de Ackermann, pero aquí se debe hacer de forma recursiva porque depende del estado estimado. Para ello, se buscó que los dos polos del observador estuvieran ubicados en -5270, que corresponde a la magnitud de los polos del sistema linealizado. Las condiciones de simulación son las mismas del caso lineal. En las Figuras 13 y 14 se observan las variables de estado reales y estimadas del convertidor boost asumiendo que existe ruido de medición en 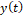 . Se evidencia una convergencia asintótica de las variables de estado sin error de estado estacionario.
. Se evidencia una convergencia asintótica de las variables de estado sin error de estado estacionario.
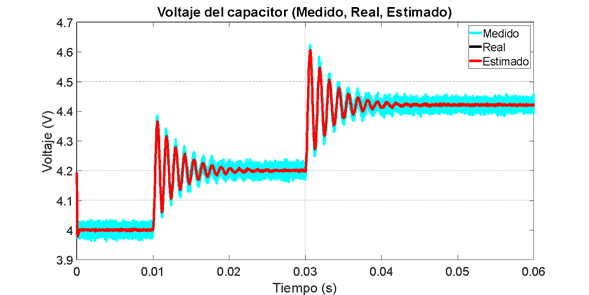
Figura 13. Estimación de Voltaje. Observador de Luenberger no lineal
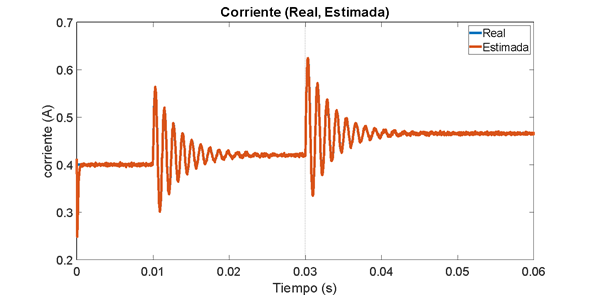
Figura 14. Estimación de corriente. Observador de Luenberger no lineal
De acuerdo con los resultados puede observarse que se elimina la desviación en los valores estimados de la corriente del inductor.
Filtro de Kalman extendido
En este caso, el filtro de Kalman utiliza el modelo no lineal de la planta para realizar la estimación a priori. Luego se calcula la matriz de covarianza del error de estimación y la ganancia de Kalman de manera similar al caso lineal, pero considerando que las matrices del modelo son el resultado de una linealización evaluadas en el estado estimado. El algoritmo se presenta a continuación.
Inicio:
- Condiciones iniciales:
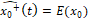 (44)
(44)
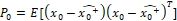 (45)
(45)
Proceso recursivo:
- Predicción:
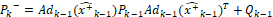 (46)
(46)
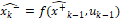 (47)
(47)
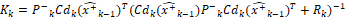 (48)
(48)
- Corrección:
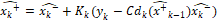 (49)
(49)
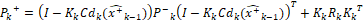 (50)
(50)
Note que en esta caso las matrices 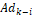 ,
, 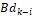 y
y 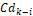 deben ser calculadas en línea como los jacobianos evaluados en el estado estimado. Adicionalmente, en este caso Q=diag(0.001^2) y R=0.01^2 debido a que se quiere evaluar la capacidad del estimador para filtrar el ruido del sistema. Las condiciones de simulación son las mismas del caso lineal y los resultados se pueden observar en las Figuras 15 y 16.
deben ser calculadas en línea como los jacobianos evaluados en el estado estimado. Adicionalmente, en este caso Q=diag(0.001^2) y R=0.01^2 debido a que se quiere evaluar la capacidad del estimador para filtrar el ruido del sistema. Las condiciones de simulación son las mismas del caso lineal y los resultados se pueden observar en las Figuras 15 y 16.
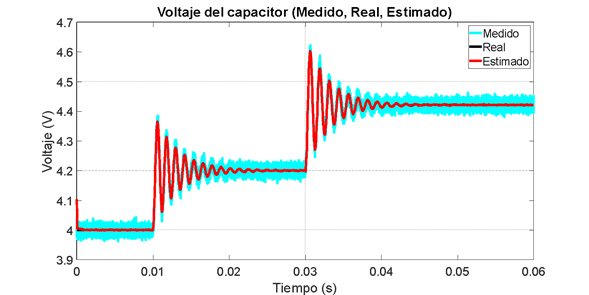
Figura 15. Estimación de voltaje con ruido. Filtro de Kalman extendido
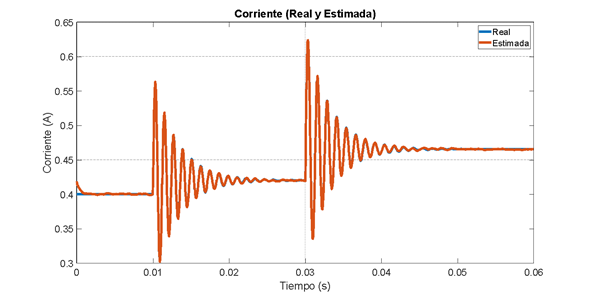
Figura 16. Estimación de corriente con ruido. Filtro de Kalman extendido
Puede notarse el trabajo que realiza el filtro para eliminar el ruido de medición y que al introducir una perturbación en la entrada D en 0.03 s, el estimador no presenta el error de estado estacionario debido a que está trabajando con el modelo no lineal.
Observador por modos deslizantes no lineal
Para el diseño del observador por modos deslizantes no lineal se utiliza el mismo modelo no lineal de la planta. La estructura del observador es entonces [3]:
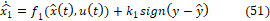
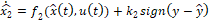 (52)
(52)
Donde 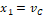 corresponde a la variable medida y
corresponde a la variable medida y 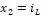 a la variable no medida. Con este observador se busca la convergencia en tiempo finito de la variable medida y luego la convergencia asintótica de la no medida. Las ganancias
a la variable no medida. Con este observador se busca la convergencia en tiempo finito de la variable medida y luego la convergencia asintótica de la no medida. Las ganancias 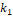 y
y 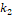 permiten ajustar las tasas de convergencia de esas dinámicas.
permiten ajustar las tasas de convergencia de esas dinámicas.
La selección de 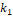 se realiza por medio de ensayo–acierto, tal que se logre la convergencia en tiempo finito del error en la parte medible del convertidor boost hacia la superficie deslizante
se realiza por medio de ensayo–acierto, tal que se logre la convergencia en tiempo finito del error en la parte medible del convertidor boost hacia la superficie deslizante 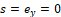 , y luego hacia el origen. A través de simulación se seleccionó la ganancia
, y luego hacia el origen. A través de simulación se seleccionó la ganancia 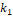 =1. Para la selección de
=1. Para la selección de 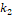 Se aplica el concepto de Filippov para encontrar la solución de una ecuación diferencial discontinua en una superficie de discontinuidad [15]. Procediendo con esto se encontró
Se aplica el concepto de Filippov para encontrar la solución de una ecuación diferencial discontinua en una superficie de discontinuidad [15]. Procediendo con esto se encontró  1000. Para la simulación de este observador se introducen las mismas perturbaciones del caso lineal. Los resultados se evidencian en las Figuras 17 a 19. En las figuras se observa que desaparece también el error de estado estacionario.
1000. Para la simulación de este observador se introducen las mismas perturbaciones del caso lineal. Los resultados se evidencian en las Figuras 17 a 19. En las figuras se observa que desaparece también el error de estado estacionario.
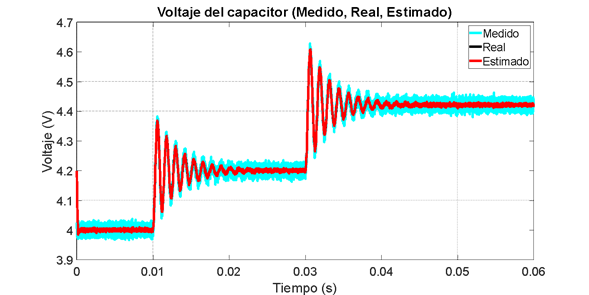
Figura 17. Estimación del voltaje. Observador por modos deslizantes no lineal
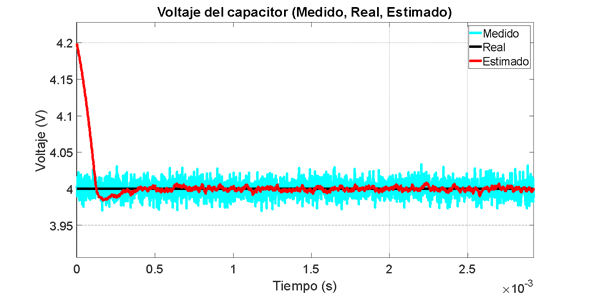
Figura 18. Convergencia en tiempo finito. Observador por modos deslizantes no lineal
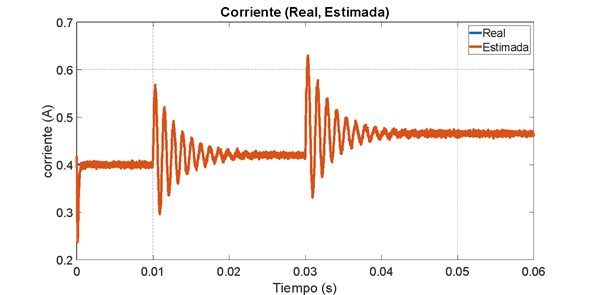
Figura 19. Estimación de la corriente. Observador por modos deslizantes no lineal
En la Figuras 17 puede verse la convergencia en tiempo finito del voltaje del capacitor en 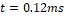 , lo cual se amplifica en la Figura 18. Así mismo, en la Figura 19 se puede observar la respuesta asintótica de la corriente con un tiempo de establecimiento aproximado 0.7
, lo cual se amplifica en la Figura 18. Así mismo, en la Figura 19 se puede observar la respuesta asintótica de la corriente con un tiempo de establecimiento aproximado 0.7 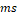 .
.
CONCLUSIONES
De acuerdo con lo realizado en el presente trabajo, fue posible encontrar un modelo lineal que representa el comportamiento de un convertidor boost alrededor de un punto de operación, y analizar algunas propiedades del modelo, de tal forma que se puedan emplear técnicas de diseño de observadores de estado lineales. Para lograr lo anterior, fue de gran importancia el modelo promediado del sistema, ya que permitió obtener un modelo lineal que fuera no singular y completamente observable.
En cuanto al diseño de los observadores lineales, se destaca que con el observador de Luenberger se logra obtener un tiempo de convergencia pequeño, pero restringido por el ruido de medición. Si la matriz de ganancias es muy grande se genera un aumento del efecto del ruido en la estimación del estado. Por otro lado, el filtro de Kalman logró un correcto rechazo de los ruidos de modelo y de medición. Sin embargo, su dinámica no se puede modificar, razón por la cual no es posible reducir su tiempo de convergencia. Por último, se diseñó un observador por modos deslizantes lineal con una dinámica rápida y modificable a partir del cambio de sus ganancias L1 y L2 y que responde de mejor manera ante el ruido en la medición. Además, se comprobó la convergencia en tiempo finito de la variable medida y la convergencia asintótica de la variable estimada. Todos los estimadores de estado lineales produjeron error de estado estacionario cuando hay cambios en el ciclo de dureza D, lo cual se explicó claramente al principio del documento.
Por lo tanto, se procedió a diseñar las versiones no lineales de estos mismos tres observadores. Pudo notarse la mejoría al incorporar el modelo no lineal en la dinámica del observador, ya que se logra eliminar el error de estado estacionario. Sin embargo, estos observadores requieren matrices jacobianas, las cuales se deben evaluar en el estado estimado en cada periodo de muestreo, lo cual genera una carga computacional alta para la implementación. Se recomienda seguir trabajando en este aspecto.
REFERENCIAS BIBLIOGRÁFICAS
[1] Firmansyah, Rifqi; Anwari, Makbul; Bouchekara, Houssem; Milyani, Ahmad; Rawa, Muhyaddin; Seedahmed, Mustafa and Budiman, Firmansyah Nur. "Control of Boost Converter Using Observer-Based Backstepping Sliding Mode Control for DC Microgrid". Frontiers in Energy Research. 10. 828978. 10.3389/fenrg.2022.828978. 2022.
[2] Oettmeier, F. M; Neely, J; Pekarek ,S; DeCarlo , R and Uthaichana, K. "MPC of Switching in a Boost Converter Using a Hybrid State Model With a Sliding Mode Observer," in IEEE Transactions on Industrial Electronics, vol. 56, no. 9, pp. 3453-3466, Sept. 2009, doi: 10.1109/TIE.2008.2006951.
[3] Wang, G; Peng, S.; Huang, H. "A Sliding Observers for Nonlinear Process Control". Chemical Engineering Sciences. Vol 52, N 5, pp 787-805, 1997. https://doi.org/10.1016/S0009-2509(96)00449-6.
[4] Cimini, G; Ippoliti, G; Orlando, G and Pirro, M. "Current sensorless solutions for PFC of boost converters with passivity-based and sliding mode control," 4th International Conference on Power Engineering, Energy and Electrical Drives, 2013, pp. 1175-1180, doi: 10.1109/PowerEng.2013.6635778.
[5] Tong, Q; Chen, C; Zhang, Q and Zou, X. "A Sensorless Predictive Current Controlled Boost Converter by Using an EKF with Load Variation Effect Elimination Function". Sensors (Basel). 2015 Apr 28;15(5):9986-10003. doi: 10.3390/s150509986. PMID: 25928061; PMCID: PMC4481978.
[6] Malekzadeh, Milad and Khosravi, Alireza and Tavan, Mehdi. (2019). "A novel sensorless control scheme for DC-DC boost converter with global exponential stability," The European Physical Journal Plus. https://doi.org/10.1140/epjp/i2019-12664-4.
[7] Dian Wang, Yu-Hong Zhao, Bo Li, Bin-Hong Li and Jia-Jun Luo, "The current observer design for buck converter," 2016 13th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), 2016, pp. 768-770, doi: 10.1109/ICSICT.2016.7999037.
[8] Cimini, Gionata; Ippoliti, Gianluca; Orlando, Giuseppe; Longhi, Sauro and Miceli, Rosario. A unified observer for robust sensorless control of DC–DC converters, Control Engineering Practice, Volume 61, 2017, Pages 21-27, ISSN 0967-0661, https://doi.org/10.1016/j.conengprac.2017.01.012.
[9] Astolfi, A and Ortega, "Immersion and invariance: a new tool for stabilization and adaptive control of nonlinear systems," in IEEE Transactions on Automatic Control, vol. 48, no. 4, pp. 590-606, April 2003, doi: 10.1109/TAC.2003.809820.
[10] Erickson, R & Maksimovic, D. Fundamentals of Power Electronics, Kluwer Academic Publishers, Second Edition, New York, 2004.
[11] Besançon, Gildas. Nonlinear Observers and Applications. Springer – Verlag. 2007.
[12] Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. John Willey. 2006.
[13] Drakunov, Sergey; Utkin, Vadmin. "Sliding Mode Observers. Tutorial". Proceeding of the 34th Conference on Decision & Control. 1995. doi: 10.1109/CDC.1995.479009.
[14] Bhattacharyya, B and Pati, K. C, "Nonlinear Controllability and Observability Analysis of DC-DC Boost Converter using Lie Algebra," 2019 International Conference on Computing, Power and Communication Technologies (GUCON), 2019, pp. 75-81
[15] Filippov, A. F. Differential Equations with Discontinuous Right hand Sides. Springer. 1988.
