AMORTIGUADORES DE MASA SINTONIZADA: UNA REVISIÓN GENERAL
Giovanni Martínez-Martínez1,2, John Jairo Blandón-Valencia3, Luis Augusto Lara-Valencia4
1 Doctorando, Universidad Nacional de Colombia, Facultad de Minas, Medellín, Colombia, yjmartinezm@unal.edu.co
2Profesor asociado Politécnico Colombiano Jaime Isaza Cadavid, Facultad Ingeniería, Medellín, Colombia, gjmartinezm@elpoli.edu.co
3 Profesor asociado, PhD, Universidad Nacional de Colombia, Facultad de Minas, Medellín, Colombia, jjblandon@unal.edu.co
4 Profesor asociado, PhD, Universidad Nacional de Colombia, Facultad de Minas, Medellín, Colombia, lualarava@unal.edu.co
RESUMEN
Las cargas que generan los eventos sísmicos y los fuertes vientos son fuerzas de la naturaleza que someten a las obras civiles a situaciones extremas, lo que provoca eventualmente la falla de las estructuras y en muchas ocasiones, la pérdida de vidas humanas. Para enfrentar estas fuerzas de carácter aleatorio y de difícil predicción, la ingeniería estructural plantea normativas de diseño y construcción de obligatorio cumplimiento en la mayoría de los países del mundo, que permiten que las estructuras puedan resistir de manera adecuada las fuerzas impuestas. Y como la historia lo ha demostrado, algunas veces un buen diseño no es suficiente, por lo que la ingeniería sismoresistente desarrolla nuevas metodologías y dispositivos que ayuden a proteger aún más a las estructuras cuando se ven sometidas a acciones como los sismos y los vientos. Para afrontar estos retos, aparecen mecanismos como los amortiguadores y controladores, agrupados como dispositivos pasivos, activos, semiactivos e híbridos, con diseños innovadores que contribuyen en gran medida a dar mayor seguridad y confianza a nuestras obras civiles. En este artículo se presenta una visión general de los amortiguadores de masa sintonizada, su desarrollo histórico, modelos mecánicos y analíticos, alcances, fortalezas y debilidades.
Palabras claves: Amortiguador Pasivo, Amortiguador Semi Activo, Magnetoreológico, Controlador, Híbrido
Recibido: 22 de febrero de 2022. Aceptado: 22 de abril de 2022
Received: February 22, 2022. Accepted: April 22, 2022
TUNED MASS DAMPERS: AN GENERAL REVIEW
ABSTRACT
The loads generated by seismic events and strong winds are forces of nature that subject civil works to extreme situations, generally causing the failure of structures and in many cases, the loss of human lives. In order to face these forces of random character and difficult to predict, structural engineering proposes design and construction regulations that are mandatory in most countries of the world, which allow the structures to adequately resist the imposed forces. And as history has shown, sometimes a good design is not enough, so seismic-resistant engineering develops new methodologies and devices that help to further protect structures when they are subjected to actions such as earthquakes and winds. In order to face these challenges, mechanisms such as shock absorbers and controllers appear, grouped as passive, active, semi-active and hybrid devices, with innovative designs that greatly contribute to give greater safety and confidence to our civil works. This article presents a general overview of seismic dampers and controllers, their historical development, mechanical and analytical models, scopes, strengths and weaknesses.
Keywords: Passive Damper, Semiactive Damper, Magnetorheological, Controller, Hybrid
Como citar este artículo: Martínez-Martínez, G., Blandón-Valencia, J., J. & Lara-Valencia, L., A. (2022) Amortiguadores de masa sintonizada: una revisión general, 18(35), 140-168. https://doi.org/10.33571/rpolitec.v18n35a10
1. INTRODUCCIÓN
Los daños presentados en las estructuras en los últimos años debido a los sismos han demostrado que es necesario realizar construcciones más seguras, que sean capaces de proteger la vida humana y que disminuyan los daños en los elementos estructurales y no estructurales.
Tradicionalmente en la ingeniería estructural, los principales criterios que se tienen en cuenta para un diseño sismo-resistente adecuado, son la rigidez lateral apropiada, la geometría regular en planta y en altura, la calidad y resistencia de los materiales, diseño detallado en las uniones, entre otros aspectos. Además, establece que la disipación de la energía debida a un sismo se debe realizar en la misma estructura y en algunos elementos sometidos principalmente a flexión mediante un comportamiento inelástico que garantice la ductilidad y la estabilidad de la estructura cuando es sometida a dichas acciones.
El campo de actuación de los sistemas de aislamiento se enfoca básicamente en desacoplar la base de una estructura del suelo, mientras que los sistemas de amortiguamiento y de control, son para contrarrestar las oscilaciones y vibraciones de las estructuras antes fuerzas externas como los sismos y los vientos. La finalidad de los amortiguadores es buscar mejorar el comportamiento de los sistemas estructurales ante cargas sísmicas y de viento, sin que esto implique un aumento de sus dimensiones o exageradas exigencias en las especificaciones de sus materiales, debido a que esto implicaría un elevado sobrecosto en el precio final de la obra. Los amortiguadores harán el trabajo de absorber y disipar la energía, logrando que la estructura presente un comportamiento elástico. Los edificios sin estos dispositivos sobreviven el sismo severo disipando energía en sus elementos principales, los que finalmente sufren el mayor daño. Si la estructura es sometida a deformaciones que puedan llegar a ser excesivas, esto se podría reflejar en un desempeño estructural deficiente, que podría conducir a situaciones altamente indeseables, tal como los elevados costos de rehabilitación por los daños en los elementos no estructurales [31].
Los amortiguadores pasivos son mecanismos externos que no necesitan de ninguna fuente de energía externa para su funcionamiento, y en ese punto radica su principal fortaleza. Este tipo de dispositivo refleja una porción de la energía del sismo que de otra forma hubiera sido disipada por la estructura en forma de daño, mediante un comportamiento inelástico.
Los amortiguadores activos requieren de una fuente de energía y un actuador para su funcionamiento, por lo que son vulnerables a cortes en el fluido eléctrico, lo que es altamente probable que ocurra durante un sismo. Incluyen en el sistema, un algoritmo de control que posee determinados parámetros susceptibles de ser ajustados para optimizar la efectividad de la acción de control. Para ejercer la fuerza de control se pueden utilizar diferentes clases de actuadores: electrohidráulicos, neumáticos y electromagnéticos [64]. Un sistema activo almacena, disipa e introduce energía al sistema por medio de actuadores, cuyo accionar es regulado a través de sensores y controladores. Los sistemas activos pueden mejorar la respuesta dinámica de una estructura, pero tienen el inconveniente que también es capaz de empeorarla, debido a que se pueden volver inestables e introducir energía cinética adicional al sistema.
Los dispositivos semiactivos difieren de los activos en que los actuadores reciben sólo un pequeño aporte de energía, por lo general proporcionado por baterías o pequeños circuitos eléctricos, y por tanto carecen de capacidad para impulsar a la estructura y son solamente capaces de frenar su movimiento. Los amortiguadores semiactivos, pueden absorber energía del sistema, pero no pueden proporcionársela.
Los sistemas híbridos son una combinación, en serie o paralelo, de los amortiguadores pasivos y activos. La eficacia de esta unión radica en que el control pasivo puede producir la mayor parte en la reducción de la respuesta mientras que el activo puede proporcionar el ajuste final, es decir, la capacidad de minimizar aún más los desplazamientos, frecuencias y aceleraciones. Con la participación de la parte pasiva, se garantiza el amortiguamiento de la estructura al instante de un evento sísmico y se evitan los inconvenientes de la demora o “delay” de la respuesta del controlador sobre la estructura, típico de los sistemas activos.
En la actualidad, la investigación en el ámbito mundial de los amortiguadores y controladores se enfoca en aspectos variados tales como la búsqueda de las ventajas y desventajas de cada uno de estos dispositivos, la propuesta de nuevos modelos acompañados de algoritmos de control novedosos y eficientes, la búsqueda de combinaciones entre los mismos amortiguadores para encontrar el dispositivo más eficiente y técnicas de optimización metaheurísticas y evolutivas de los parámetros que conforman los modelos matemáticos de los diferentes dispositivos.
2. AMORTIGUADOR DE MASA PASIVO SINTONIZADO
El amortiguador pasivo de masa sintonizada o TMD (Tuned Mass Damper), es un dispositivo que puede ser modelado como un sistema de dos grados de libertad, el cual consiste básicamente en una masa unida a un resorte y a un amortiguador, cuyo propósito es atenuar las vibraciones y desplazamientos laterales de la estructura, en especial cuando el TMD se sincroniza con la frecuencia natural de la estructura.
La frecuencia natural del amortiguador TMD se diseña lo más cerca posible de la frecuencia natural del sistema principal (edificio, torre de energía, puente, etc.) provocando que el amortiguador vibre en resonancia, disipando la energía absorbida a través de los mecanismos propios del TMD. En resumen, los TMD sólo pueden ser diseñados a una sola frecuencia estructural, lo que constituye su principal desventaja. Este problema se puede subsanar en gran parte, ubicando varios TMD en diferentes posiciones y alturas, logrando con esto, tener varios TMD sintonizados a diferentes frecuencias. La masa contenedora puede ser sólida o líquida y el recipiente contenedor de variada geometría. Entre los dispositivos de masa líquida se encuentran los TLCD (Tuned Liquid Column Damper), en la cual el tanque receptor tiene forma de U y los TLSD (Tuned Liquid Sloshing Damper), cuyo tanque receptor tiene geometría rectangular.
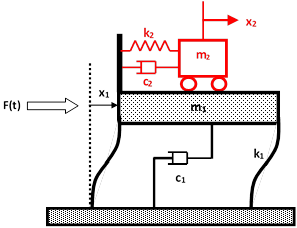
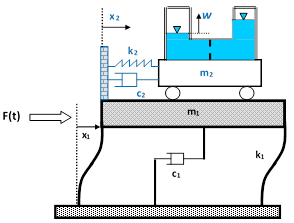
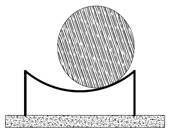
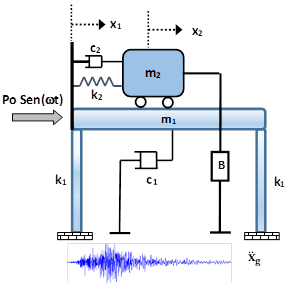
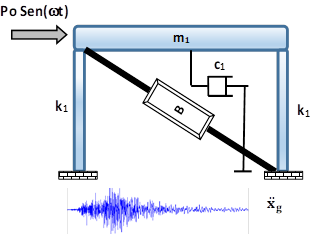
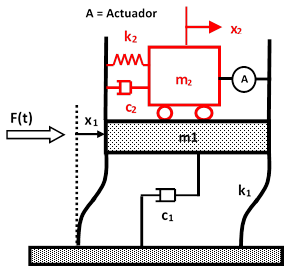
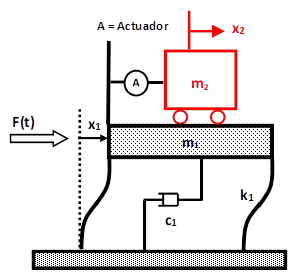
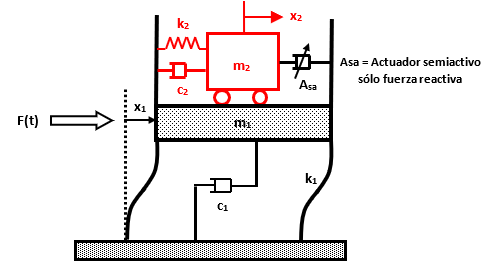
En la figura 1 se muestra la representación básica de un TMD pasivo, de donde se desprende el modelo matemático básico antes de incursionar en sistemas de varios grados de libertad. La estructura es un sistema de dos grados de libertad, donde la estructura principal con su masa, rigidez y amortiguamiento está unida a otro sistema (masa amortiguadora) con sus propias características. En la figura 1(a) la masa superior es sólida, comúnmente llamado TMD, y en la figura 1(b) la masa superior es líquida, con el tanque receptor en forma de U, más conocido como TLCD. En el TLCD, el amortiguamiento se presenta cuando el líquido en su recorrido dentro del recipiente se ve abruptamente frenado por una válvula de control en la sección horizontal.
|
|
|
|
(a) |
(b) |
Figura 1 Esquema general de un amortiguador de masa pasivo: (a) TMD (b) TLCD
Donde:
m1, m2 = Masa de la estructura y de la masa amortiguadora respectivamente.
k1, k2 = Rigidez de la estructura y de la masa amortiguadora respectivamente.
c1, c2 = Constante de amortiguamiento de la estructura y de la masa amortiguadora respectivamente.
F(t) = Carga en la estructura.
Si la carga es armónica F(t) = Po sen(wt)
Si la carga es de sismo F(t) = -m1 ẍg
w = Frecuencia de la fuerza excitatriz.
ẍg = aceleración del sismo
El modelo matemático que describe el comportamiento del TMD o TLCD, se muestra en las ecuaciones (1) y (2). La ecuación (1) es para carga armónica en la estructura y la ecuación (2) es para carga de sismo.
|
|
(1) |
|
|
(2) |
Las ecuaciones (1) y (2) son la base para el estudio de la mayoría de los amortiguadores de masa sintonizada y su análisis permite conocer las fortalezas, debilidades y posibilidades de este tipo de amortiguadores. Las primeras investigaciones encontraron que, si se desprecia el amortiguamiento en la estructura y en el TMD o se desprecia únicamente el amortiguamiento de la estructura, se pueden obtener soluciones analíticas en el cálculo de los valores óptimos de los parámetros que conforman ambas ecuaciones y que permitiría minimizar de manera óptima el desplazamiento o las vibraciones de la estructura. Tener en cuenta el amortiguamiento del TMD y de la estructura (ecuaciones 1 y 2) es el modelo más completo posible, pero a la vez es el más complejo de solucionar, por lo que se debe recurrir a los métodos numéricos para encontrar los parámetros óptimos. Los parámetros de diseño del TMD para lograr la máxima eficiencia, son la relación de frecuencias (frecuencia del TMD/frecuencia de la estructura), la relación de amortiguamiento (amortiguamiento del TMD/amortiguamiento del edificio) y principalmente, la relación de masas (masa del TMD/masa de la estructura)
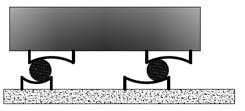
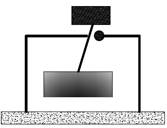
Existen diferentes modelos de TMD, cada uno cumpliendo una labor especifica. Matta y De Stefano [70] muestran un resumen para varios tipos de estos dispositivos. Ver figura 2.
|
|
|
|
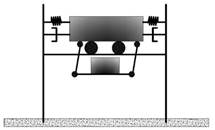
(b) Péndulo de rodillo |
|
|
|
|
|
(c) Péndulo simple |
(d) Aisladores de goma |
(e ) Péndulo de balancín |
|
|
|
|
|
(f) Péndulo de barra rígida |
(g) Péndulo de bola |
(h) Masa doble con rigidez y amortiguamiento |
Figura 2 Modelos de TMD según Matta y De Stefano [70]
El concepto de amortiguador de vibración sintonizado (Tuned Vibration Absorbers o TVA), fue introducido por primera vez por el alemán Hermann Frahm [32], bajo la patente #989958 del 18 de abril de 1911, en los EEUU.
Posteriormente, Ormondroyd y Den Hartog [79], publican el artículo, The theory of dynamic vibration absorber, en el Journal of Applied Mechanics, Trans. ASME, Vol. 49, pp. A9-A22, siendo este documento el punto de partida dentro de las publicaciones del siglo XX [4]. Años más tarde, el mismo Den Hartog [28], publica el libro Mechanical Vibrations, donde se muestran las aplicaciones en el campo de la industria de los amortiguadores de masa a través de modelos de uno y dos grados de libertad, derivando expresiones para el amortiguamiento óptimo, siendo esta una de las referencias bibliográficas más citadas.
Varios autores han contribuido al desarrollo del TMD. Luft [65], planteó expresiones aproximadas para el diseño de los parámetros que conforman las expresiones del TMD. McNamara [69], estudió de manera profunda, los alcances y bondades del TMD pasivo como sistema de dos grados de libertad en edificios altos. Ayorinde y Warburton [5] y Warburton y Ayorinde [109] trataron el tema general de los amortiguadores y sobre la optimización de los parámetros más importantes del TMD.
Kwok [53], propuso en sus estudios aumentar el amortiguamiento en edificios por medio de los TMD. Kitamura et al. [52] muestran el proceso de análisis y diseño del Chiba Port Tower (Tokio, Japón), una estructura de acero de 125 metros de altura con dos TMD en su parte superior. Sakai et al. [91] son pioneros en tratar el tema del amortiguador de columna líquida TLCD (Tuned Liquid Colum Damper).
Balendra et al. [6] estudiaron el tema de la efectividad del TLCD como amortiguador. Kareem et al. [48] presentaron un breve resumen con las primeras estructuras a nivel mundial que se potenciaron haciendo uso del TMD.
Li y Liu [59] estudiaron la optimización de los parámetros de múltiples TMD en un edificio. Por su parte, Ricciardelli et al. [2003] someten un edificio a cargas de viento y con tres tipos de amortiguadores: un TMD pasivo, un TMD semiactivo y un TMD híbrido. Borgues et al. [12] realizan el estudio paramétrico de múltiples TMD utilizando masas interconectadas, mientras que Sgobba y Marano [94] diseñan de manera lineal los TMD ubicados en estructuras con comportamiento no lineal. Gutiérrez y Adeli [41], presentan un estudio amplio y actualizado de las estructuras a nivel mundial con TMD como amortiguador.
Lin et al. [63] hacen una comparación de los resultados hallados entre los modelos analíticos y los modelos experimentales usando TMD. Raveesh y Sahana [85], realizan una revisión bibliográfica de los TMD pasivos, y desarrollan un ejercicio que consiste en la modelación de un edificio en SAP2000 v15 añadiéndole un TMD mediante un artificio de modelación y comparando los resultados hallados con los de la modelación numérica convencional para este tipo de dispositivos. Meena et al. [71] plantean la optimización de los parámetros del TMD por medio de métodos analíticos y del efecto de la presencia de múltiples TMD. Kaveh et al. [49], Nigdeli et al. [77][78] y Yazdi et al. [113] optimizaron los parámetros del TMD por medio de técnicas heurísticas, metaheurísticas y evolutivas, buscando la máxima eficiencia del amortiguador. Zhou et al. [119] elaboraron un estudio para comprobar la efectividad del TMD en edificios de baja y mediana altura sometidos a sismos.
Garrido y Serrazin [35], analizaron la efectividad del TMD en los recientes sismos en Chile. Altunişik et al. [2], realizaron un estudio experimental del TLCD sometido a diferentes excitaciones. Ata y Kamel [3], desarrollaron un análisis numérico del efecto combinado de un TMD clásico traslacional y un TMD tipo péndulo. Cetin y Aydin [17], proponen una nueva función de transferencia y como técnica numérica para encontrar los parámetros óptimos, la evolución diferencial. Rahmani y Konke [88], analizaron el uso de múltiples TMD para el control sísmico de edificios altos sometidos a cargas de sismo.
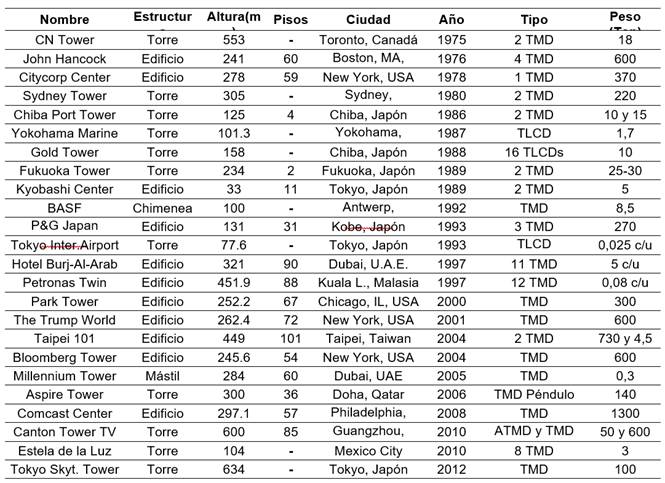
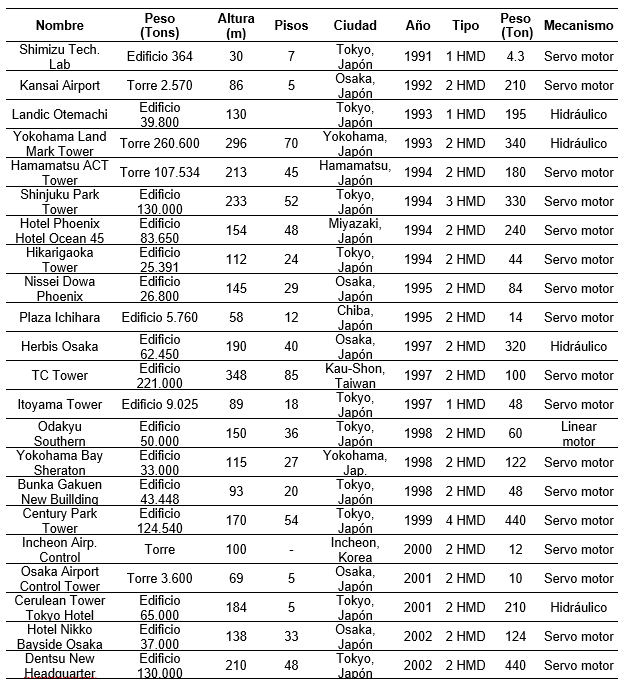
En la tabla No 1 se puede apreciar la recopilación que elaboran Gutiérrez y Adeli [41], sobre las estructuras más importantes a nivel mundial que utilizan como amortiguador un TMD de masa sólida o líquida.
En la figura 3(b), el Taipei 101, uno de los edificios más altos del mundo que hace uso de un TMD en forma de péndulo para disminuir los desplazamientos laterales debido a los fuertes vientos. En la figura 3(c), el edificio One Rincon Tower de la ciudad de San Francisco, EEUU., con un amortiguador TLSD ubicado en la parte superior de la edificación. En este tipo de TMD, el tanque receptor es rectangular y el amortiguamiento se presenta cuando el agua en su recorrido choca contra las obstrucciones o persianas. En la figura 3(d), la chimenea de la empresa BASF Química en Antwerp, Bélgica, donde se ubicó un TMD de 8.5 toneladas en la parte superior para el control de los desplazamientos.
Tabla 1 Estructuras con TMD (Gutiérrez y Adeli [41])
|
|
|
|
(a) Chiba Port Tower, Tokyo Bay, Japan
|
(b) Taipei 101, Taiwan
|
|
|
|
|
(c) One Rincon Tower (San Francisco) - TLSD pasivo
|
(d) Chimenea de BASF Química, Bélgica
|
Figura 3 Estructuras construidas o repotenciadas con TMD
3. AMORTIGUADOR DE MASA PASIVO SINTONIZADO INERTER
Un nuevo tipo de TMD pasivo que apareció hace poco como tema de investigación, es el llamado amortiguador de masa sintonizado inerter o TMDI (Tuned Mass Damper Inerter), cuyas primeras aplicaciones fueron para la suspensión de los carros de carreras desarrolladas para la Fórmula I. Cuando no se utiliza la masa del TMD y solo el dispositivo Inerter, se llama TID (Tuned Inerter Damper).
La idea general de este amortiguador fue desarrollada por Smith [95] y básicamente se define como un mecanismo de dos nodos o dos terminales, con la propiedad de que fuerzas iguales y opuestas aplicadas en los nodos, son proporcionales a la aceleración relativa entre los nodos. Ver figura 4.
 |
Figura 4 Esquema general de un TMDI
De esta figura se observa que la fuerza aplicada en los extremos depende de la constante de proporcionalidad b, llamada la Inertancia, y que tiene unidades de masa. La energía almacenada en el Inerter es ½ b (a2-a1)2, donde a1 y a2 son las aceleraciones de las masas de los extremos.
Para que este dispositivo sea útil y práctico debe cumplir ciertas condiciones:
a) Poseer una masa pequeña, independiente del valor de la fuerza inercial requerida.
b) No es necesario conectar ningún punto del dispositivo al suelo de apoyo.
c) Tener un comportamiento adecuado en cualquier orientación espacial y movimiento.
d) Tener un comportamiento lineal en su funcionamiento que se especifica desde el principio.
En la figura 5 se muestra el modelo de dos grados de libertad de un TMDI según Pietrosanti et al. [82] y en la figura 6 un sistema de varios grados de libertad con un TMDI en la parte superior, según Giaralis y Marian [38].
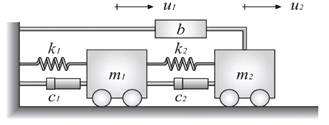
Figura 5 Esquema general de un TMDI (Pietrosanti [82])
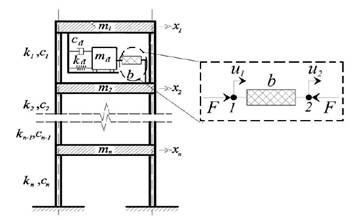
Figura 6 Esquema general de un TMDI (Giaralis y Marian [38])
El esquema general de un TMDI y un TID, se puede ver en la figura No 7:
|
|
|
|
(a) |
(b) |
|
Figura 7 Esquema general de un amortiguador de masa pasivo inerter: (a) TMDI (b) TID |
|
La ecuación de la dinámica que describe el comportamiento del TMDI, se muestra en las ecuaciones (3) y (4). La ecuación (3) es para carga armónica en la estructura y la ecuación (4) es para carga de sismo.
|
|
(3) |
|
|
(4) |
Si se compara con las ecuaciones (1) y (2) la diferencia radica en la presencia del término b (Inertancia). Al igual que con las ecuaciones (1) y (2), se pueden obtener soluciones analíticas si de desprecia los amortiguamientos del TMDI y de la estructura.
El estudio y desarrollo del TMDI básicamente comienza hacia el año 2010. Takewaki et al. [104] presentan las primeras aplicaciones del TMDI en estructuras aporticadas, estudiando un pórtico plano de tres pisos. Posteriormente. Lazar et al. [56][57] desarrollan de manera detallada el procedimiento matemático de este amortiguador y sus futuras aplicaciones y alcances en el mundo de los controladores pasivos. Marian y Garalis [68] analizan la configuración del TMDI cuando es sometido los apoyos a una excitación de carácter estocástico.
Giaralis y Taflanidis [37] diseñaron un TMDI en un edificio de varios pisos sometidos a excitaciones sísmicas. Brzeski et al. [14] analizaron la dinámica y la aplicación de un TMDI y especialmente se detalla el estudio de un mecanismo interno del Inerter, llamado T-shaped pendulum. Giaralis y Marian [38] usan el Inerter como una forma de aumentar la efectividad del dispositivo en la reducción de los desplazamientos y vibraciones de las edificaciones sin la necesidad de instalar más TMD, lo que contribuye finalmente a no aumentar la masa de los amortiguadores.
Wen et al. [110], evaluaron el TID como control sísmico de estructuras de varios grados de libertad. Zhang et al. [116][117], tratan el tema del uso TID en estructuras tipo edificios de varios pisos de altura y el efecto de múltiples TID en sistemas de múltiples grados de libertad.
Hu et al. [43] y Pietrosanti et al. [82], contribuyeron de manera notable en los aspectos físicos y matemáticos del TMDI y su futura influencia como un excelente amortiguador, económico y eficiente. Giaralis y Petrini [39] utilizaron el TMDI para reducir los desplazamientos en edificios sometidos a fuertes cargas de viento. Barredo et al [8], obtienen soluciones analíticas para obtener un diseño óptimo en el control de las vibraciones utilizando TID. Ruiz et al. [89] estudiaron la optimización basada en riesgo del TMDI para la protección sísmica de edificios de varios pisos.
Taflanidis et al. [103], tratan el tema del diseño multiobjetivo de TID para el control de las vibraciones y proteger de los efectos del sismo en edificios de varios pisos. Radu et al. [87] trabajaron el tema del diseño sísmico basado en desempeño utilizando TID. Cao y Li [16], estudiaron el tema de múltiples TID trabajando en conjunto en estructuras sometidas a excitaciones en la base tipo ruido blanco.
4. AMORTIGUADOR DE MASA ACTIVO
Los amortiguadores activos son dispositivos que requieren de una fuente de energía para su funcionamiento y subsanan en parte las debilidades de los sistemas pasivos, como la de permitir ser sintonizados a una amplia gama de nuevas frecuencias. El activo es un amortiguador con la presencia de un actuador en la masa superior, que es activado desde un computador con un algoritmo de control especializado que envía señales de acuerdo con la respuesta estructural, para de esta forma generar nuevas frecuencias y poder contrarrestar de manera eficiente los desplazamientos de la estructura. Pero en contrapartida exigen algoritmos computacionales algunos de ellos bastantes complejos que los alejan del campo de aplicación de la ingeniería práctica. La forma en que actúa este actuador en la masa amortiguadora es lo que diferencia a los amortiguadores activos de los semiactivos.
La fuerza que aplica el actuador a la estructura es un proceso que opera en tiempo real. Es decir, cuando el edificio es sacudido por un sismo o una fuerza del viento considerable, unos cuantos sensores miden la respuesta de la estructura. Estas medidas son digitalizadas y recibidas por un ordenador que implementa un algoritmo de control. Este algoritmo calcula el valor de desplazamiento necesario y gobierna el mecanismo de los actuadores, que se encargan de transformar la señal en una fuerza efectiva.
En líneas generales, un amortiguador activo:
· En lugar de dispositivos inertes (disipadores) se colocan mecanismos activos (actuadores) alimentados por fuentes de energía, de forma que son capaces de “empujar” vigorosamente a la estructura para intentar contrarrestar el efecto de la excitación.
· Se instalan sensores que permiten conocer en tiempo real la situación de la estructura (desplazamiento, velocidad y aceleración) y esta información es procesada por un controlador (software instalado en un computador) el cual decide qué hacer, transmitiendo a los actuadores las órdenes precisas para que éstos ejecuten acciones sobre la estructura de la forma más eficaz posible, con el fin de reducir su respuesta (López y Bozzo, 2003).
En la figura 8(a) se puede apreciar el esquema básico de un amortiguador activo de masa sintonizada (Active Tuned Mass Damper o ATMD). En este modelo, la fuerza inercial de la masa amortiguadora solo actúa cuando el actuador recibe la señal del controlador. En la figura 8(b) se aprecia el Active Mass Damper (AMD), otro tipo de sistema de control activo, el cual es una masa auxiliar móvil usualmente inferior al 1% de la masa total de la estructura y es instalada en una de las últimas plantas del edificio, con un actuador conectado a ella. La fuerza inercial que presenta la masa oscilante más la fuerza adicional que transmite el actuador debe contrarrestar los efectos de la acción sísmica y reducir la respuesta estructural a valores aceptables (Villareal y Oviedo [107]).
|
|
|
|
(a) |
(b) |
Figura 8 Amortiguador de masa activo: (a) ATMD (b) AMD
En la figura 9, el diagrama de flujo de su funcionamiento, según Cheng et al. [20].
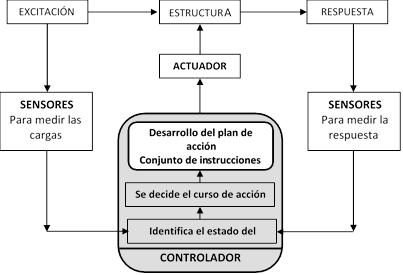
Figura 9 Diagrama de flujo del funcionamiento de un ATMD (Cheng et al. [20])
Algunos amortiguadores activos funcionan de forma diferente y abarcan una amplia variedad de dispositivos y enfoques de control [33]. Uno de los primeros ejemplos de control activo es el sistema de tendón activo ATS (Active Tendon System) que utiliza tendones pretensados unidos a la estructura para controlar las respuestas. Los actuadores pueden variar la tensión en los tendones dependiendo del comportamiento medido en la estructura para disminuir la respuesta global a la excitación.
El control activo presenta muchas ventajas inicialmente. Debido a la naturaleza de operación que es en tiempo real, los sistemas activos son bastante versátiles con la capacidad de adaptarse a situaciones cambiantes y alterar patrones de carga. Con esta adaptabilidad, los sistemas de control activo a menudo pueden proporcionar reducciones de respuesta muy superiores a las de los sistemas pasivos. Además, debido a que el sistema de control es flexible, se pueden alcanzar múltiples objetivos de rendimiento. El objetivo principal se puede enfatizar para disminuir la deriva de piso, o si la idea central es que la estructura sufra los mínimos daños después de un acontecimiento sísmico. Por el contrario, si la estructura está llena de equipos delicados, la reducción de la respuesta de aceleración de la estructura podría ser primordial.
Morison y Karnopp [73] desarrollaron las primeras comparaciones entre el amortiguador activo y el pasivo, para poder determinar las ventajas y desventajas de cada modelo. Chang y Soong [19]. muestran a través de ejemplos numéricos sencillos, la reducción de los desplazamientos y aceleraciones, mediante la adición de componentes activos en un TMD. Miller et al. [72] emplearon el amortiguador activo en estructuras de edificios de gran altura, proponen estrategias de control y estudios de simulación digital para determinar la robustez del modelo propuesto.
Cao et al. [15] diseñaron un amortiguador activo para controlar los desplazamientos y aceleraciones de una torre de televisión de 340 metros de altura en Nanjing, China, debido a los fuertes vientos. Balendra et al. [7] hacen uso del TLCD como amortiguador activo para reducir los desplazamientos de edificios sometidos a fuertes cargas de viento. Li et al. [61] propusieron el uso de múltiples TMD activos como estrategia para mejorar el rendimiento del amortiguador activo, variables como la relación de frecuencias, relación de masas, número de amortiguadores, etc., son tenidas en cuenta. Lee [58] utiliza un amortiguador activo para reducir la respuesta de edificios y tiene en cuenta la interacción suelo-estructura.
Nazarimofrad y Zahrai [75], utilizaron tendones activos para el control sísmico de estructuras irregulares de varios pisos y considerando la interacción suelo estructura. Kim et al. [51] emplearon el algoritmo LQR en un ATMD para controlar la respuesta a los vientos de edificios altos. Li y Cao [62] analizan múltiples ATD trabajando en conjunto para el control sísmico de estructuras.
Gran parte de la investigación en los sistemas activos se ha enfocado en los algoritmos de control que son los que envían la señal al actuador, señal que es enviada desde un computador que recibe los datos de la respuesta estructural del edificio cuando es excitado por el movimiento sísmico o las cargas de viento.
Nishimura et al. [76], Chang y Yang [18] y Lee [58] emplean los métodos lineales como técnica numérica para desarrollar el algoritmo del controlador. Dyke [29] emplea los métodos lineales, pero incluyendo el control de la salida que se retroalimenta de la aceleración del edificio. También los métodos no lineales como los métodos de redes neurales, Ghaboussi y Abdolreza [36]. Los métodos basados en lógica difusa, Yoshimura et al. [114] y en los algoritmos genéticos, Jiang y Hojjat [46]. Cada método o algoritmo está diseñado para aumentar la eficacia del sistema de control global.
A pesar de su potencial, los sistemas activos son difíciles de implementar en la práctica, por ese motivo, una parte importante de la investigación se concentra en el desarrollo de estrategias de control semiactivos e híbridos. La gran demanda de energía que exige su actuación ante un sismo severo y la complejidad de los algoritmos de control los convierte en sistemas poco aplicables en la práctica.
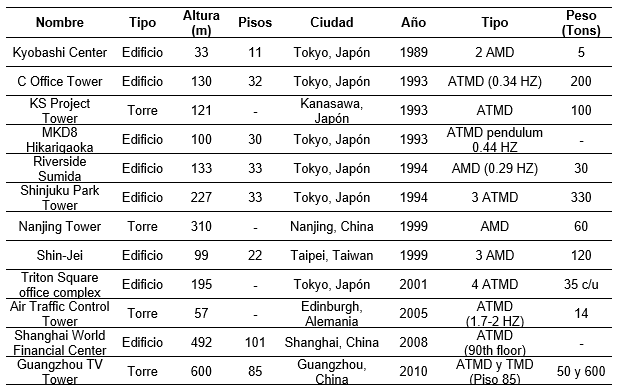
Gutiérrez y Adeli [41], presentan un estudio de estructuras a nivel mundial con la presencia de amortiguadores de masa activos. En la tabla 2 un resumen.
Tabla 1 Estructuras con amortiguadores de masa activos (Gutiérrez y Adeli [41])
En la figura 10, ejemplo de un amortiguador de masa activo sintonizado, que se ubica por lo general en los pisos superiores de los edificios. Se observa la masa formada por varias capas de acero, los rieles donde se mueve el amortiguador y el circuito eléctrico del dispositivo.
En la figura 11(a) se puede apreciar la torre de control del aeropuerto de Edinburgh, Alemania, con un amortiguador de masa activo en su parte superior. En la figura 11(b) el edificio Riverside Sumida en Tokyo, Japón, con un amortiguador activo de 30 toneladas en su parte superior.
 |
Figura 10 Amortiguador de masa activo
|
|
|
|
(a) Torre de control, Edinburgh, Alemania
|
(b) Edificio Riverside Sumida, Tokyo, Japón
|
Figura 11 Estructuras con amortiguador de masa activo
5. AMORTIGUADOR DE MASA SEMIACTIVO
Los amortiguadores de control semi-activo, SATMD por sus siglas en inglés (Semi Active Tuned Mass Damper), son dispositivos que no requieren de grandes fuentes de potencia debido a que pueden trabajar con baterías u otro tipo de mecanismos magnéticos, lo que se convierte en una gran ventaja debido a que durante un sismo puede llegar a fallar el suministro de energía eléctrica.
Los dispositivos de control semi-activo pueden ser operados en tiempo real y a diferencia de los dispositivos activos, los semi-activos no pueden incrementar energía mecánica a la estructura que se desea controlar. Estos dispositivos de control tienen propiedades que se pueden variar de forma dinámica permitiendo absorber de manera efectiva la energía proveniente de las vibraciones, reduciendo de esta forma, la respuesta de la estructura bajo una gran variedad de condiciones de cargas dinámicas [40].
Los sistemas semiactivos tienen un esquema de funcionamiento muy similar a los sistemas activos, diferenciándose de estos en que el control estructural se obtiene a partir de dispositivos de carácter reactivo, cuyas características mecánicas (rigidez o amortiguamiento) son controlables, lo cual permite modificar las propiedades dinámicas de la estructura con costos energéticos muy reducidos [107].
En otras palabras, en los sistemas semiactivos, los actuadores reciben sólo un pequeño aporte de energía (por lo general proporcionada por acumuladores eléctricos de reducido tamaño o baterías) y por tanto carecen de capacidad para impulsar a la estructura y son solamente capaces de frenar su movimiento, es decir, pueden absorber energía del sistema, pero no pueden proporcionársela [64]. Estos sistemas son más sencillos, robustos, fiables y económicos que los activos y su rendimiento es solo ligeramente inferior y superior al de los puramente pasivos.
En la figura 12 se muestra el esquema general de un amortiguador semiactivo, un sistema de dos grados de libertad, pero con la presencia de un actuador en la masa amortiguadora, cuya función no es proporcionar energía al sistema, sino la de contrarrestar el movimiento lateral de la estructura. En la figura 13 un diagrama de flujo de su funcionamiento.
Figura 12 Esquema general de un amortiguador de masa semiactivo sintonizado (SATMD)
Hrovat et al. [42], propusieron un amortiguador semiactivo con un actuador hidráulico y comparan los resultados con los de un amortiguador pasivo. Tanaka y Kikushima [105] presentaron un amortiguador semiactivo para controlar las vibraciones ocasionadas por un impacto. Abé e Igusa [1] proponen un algoritmo de control con expresiones simples y amortiguamiento ajustable en tiempo real. Symans y Constantinou [102] elaboran un estado del arte de este tipo de dispositivos.
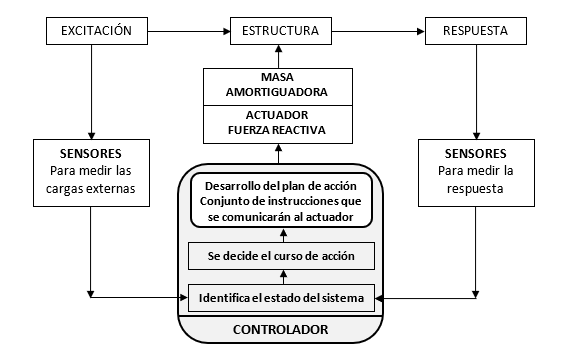
Figura 13 Diagrama de flujo del funcionamiento de un SATMD (Cheng et al. [20])
Pinkaew y Fujino [83] analizaron la efectividad del amortiguador semiactivo bajo excitaciones armónicas. Yalla et al. [111] y Sonmez et al. [97] utilizan un TLCD como amortiguador semiactivo para el control de vibraciones. Sun et al. [101] realizan un estudio experimental de amortiguadores semiactivos en edificios utilizando mesas vibradoras. Ji et al. [45] presentan el estudio de la efectividad de un amortiguador semi activo y para ello utilizan cuatro algoritmos de control diferentes: displacement based groundhook (DBG), velocity based groundhook (VBG), clipped optimal y maximum energy dissipation (MEDA).
Chey et al. [21] plantearon el uso del amortiguador de masa semiactivo en un sistema de edificios. Pastia y Luca [80] utilizaron un dispositivo semiactivo con amortiguamiento variable paran el control de las vibraciones de edificios sometidos a excitaciones armónicas y de sismo. Chung et al. [22] presentaron un estudio que propone una innovadora metodología del control de fase para los amortiguadores de masa sintonizados semiactivos.
Kerboua et al. [50] realizaron un estudio analítico y numérico de este tipo de dispositivos. Demetriou et al. [27] proponen un algoritmo de control simple en amortiguadores semiactivos para aplicarlo a edificios. Soliman et al. [96] emplean un TLD como un dispositivo semiactivo.
El amortiguador semiactivo que más se ha destacado en los últimos años y que más expectativas genera, es el llamado amortiguador semiactivo magnetoreológico, qué por su condición especial e importancia, se tratará con más amplitud en el siguiente capítulo.
6. AMORTIGUADOR SEMIACTIVO MAGNETOREOLÓGICO (MRD)
De los dispositivos semiactivos que más se han destacado en los últimos años, son los llamados de fluido controlables, denominados amortiguadores electroreológicos o ED (Electrorheological Damper) y los amortiguadores magnetoreológicos o MRD (Magneto Rheological Dampers), siendo este último el más conocido.
La reología es la ciencia que estudia la deformación de la materia cuando está sometidas a fuerzas. Esta ciencia se limita básicamente a materiales que no obedecen a la ley de viscosidad de Newton ni a la ley de Hooke [24]. El amortiguador electroreológico está compuesto de un cilindro hidráulico que contiene micro partículas dieléctricas suspendidas en un fluido. Cuando dicho fluido es sometido a la presencia de una corriente eléctrica las partículas se polarizan y el fluido se vuelve sólido en cuestión de milisegundos, ofreciendo un incremento de la resistencia del fluido.
Los amortiguadores magnetoreológicos (ver figura 3.19) son los análogos magnéticos de los amortiguadores electroreológicos, las partículas suspendidas en el fluido se alinean cuando se le somete a la presencia de un campo magnético. Estos amortiguadores cuentan con electro magnetos ubicados dentro de la cabeza del pistón para generar el campo magnético (Jiménez, 2006).
Los MRD son dispositivos de control semi-activo altamente no-lineal compuesto por un cilindro hidráulico, bobinas magnéticas y un fluido estimulable denominado fluido magnetoreológico, que consiste de partículas magnéticamente polarizables suspendidas en un medio oleoso, cuya principal particularidad es su habilidad para cambiar, de manera reversible, de un estado líquido lineal viscoso de libre flujo para un estado semi-sólido en milisegundos, cuando es expuesto a un campo magnético [30] [54].
El comportamiento de los fluidos magnetoreológicos depende de numerosos factores como son la temperatura, la interacción entre partículas, la concentración de estas, fenómenos de sedimentación, forma y volumen de las partículas, viscosidad del fluido portador, etc. Esta peculiaridad hace de los MRD una herramienta ideal para el control de sistemas estructurales, pues con ellos es posible cambiar las fuerzas de amortiguamiento de forma simple, rápida y segura a un costo relativamente bajo. En la figura 14 se muestra un MRD típico, un elemento tipo barra con una cápsula en el centro donde se almacena el líquido magnetoreológico.
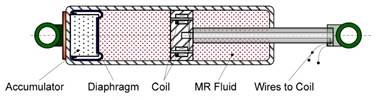

Figura 14 Modelo de amortiguador semiactivo Magnetoreológico
En la figura 15 se aprecia un par de MRD de 25 cm de longitud pertenecientes a la Universidad Nacional de Colombia, sede Medellín, amortiguadores que se colocaron en la parte inferior de un modelo 3D, que está ubicado en una mesa vibradora, sometida a diferentes acelerogramas de sismos conocidos. Los amortiguadores, el modelo 3D, la mesa vibradora y demás equipos, hacen parte de los trabajos de experimentación que viene realizando el grupo de investigación de ingeniería civil de la universidad. Ver figura 16.


Figura 15 Amortiguadores magnetoreológicos para experimentación
|
|
|
Figura 16 Montaje experimental de amortiguador magnetoreológico
Spencer et al. [98] analizaron al MRD como un nuevo enfoque para la protección sísmica de estructuras. Dyke [29] y Dyke et al. [30] presentan el modelamiento matemático de un MRD utilizando el modelo de Bouc-Wen para el ciclo de histéresis del amortiguador y proponen una nueva estrategia de selección de señal llamada clipped-optimal. Spencer et al. [99] presentan el denominado modelo fenomenológico de los MRD y comparan los resultados del modelo con los de la experimentación por medio de un prototipo.
Jansen y Dyke [44] presentaron el resultado de un estudio que evalúa el comportamiento de varios algoritmos de control propuestos a la fecha con múltiples MRD. Yang et al. [112] desarrollaron el modelamiento y el comportamiento dinámico de un MRD a escala real. Wang et al. [108] empelaron un TLCD con fluido magnetoreológico y aplican el modelo propuesto en un edificio de 50 pisos y 162 metros de altura. Datta [25] describe detalladamente este tipo de amortiguador y sus componentes más importantes.
Setareh et al. [93] estudiaron un MRD en forma de péndulo para controlar las excesivas vibraciones de los pisos de los edificios. Bitaraf et al. [11] emplearon el MRD como estrategia para la protección sísmica de los edificios y emplean dos estrategias de control, el Simple Adaptive Control y el fuzzy control basado en genética. Braz-César y Barros [13] presentan los resultados numéricos y experimentales del comportamiento no lineal del MRD y emplean tres modelos de histéresis, el modelo de Bingham, el de Bouc-Wen y el de Bouc-Wen modificado.
Lara et al. [54] analizaron la respuesta estructural de un edificio tipo pórtico de dos pisos controlado por un par de MRD, administrados por un regulador lineal cuadrático (LQR) asociado con el controlador clipped optimal. Zemp et al. [115] plantearon un estudio sobre este tipo de amortiguadores e incluyen una propuesta de estudio sobre un MRD que se utilizó en un edificio real en Santiago de Chile.
Peng et al. [81] presentaron un estudio numérico-experimental del MRD basado en el ciclo de histéresis de Bouc-Wen-Baber-Noori (BWBN). Lara et al. [55] hacen uso de la lógica difusa como algoritmo de control, el cual realiza ajustes en la señal de forma simple y rápida basado en el conocimiento heurístico que se tenga de la estructura. Bathaei et al. [9] combinan un TMD con un MRD en un edificio de 11 pisos y emplean como controlador la lógica difusa.
El amortiguador magnetoreológico es uno de los actuadores semiactivos más prometedores, debido a que necesitan de muy poca energía para su funcionamiento y pueden operar hasta con baterías, son compactos, confiables, relativamente económicos, responden rápidamente y es factible implementarlos en una estructura de tamaño real. El fluido magnetoreológico tiene características atractivas como una buena fluencia, baja viscosidad, comportamiento estable con histéresis ante un gran rango de temperaturas, es insensible a los contaminantes por lo que facilita y reduce el costo de su producción, y en especial, en la gran fluencia debida a la densidad de energía magnética que se puede establecer en el fluido.
A pesar de sus grandes ventajas, la naturaleza no lineal del líquido magnetoreológico hace que el diseño de un algoritmo de control adecuado que pueda sacar provecho de sus características únicas sea una tarea bastante compleja.
7. AMORTIGUADOR DE MASA HIBRIDO (HMD)
Los controladores de masa híbridos o HMD (Hybrid Mass Damper) son una combinación de los sistemas pasivos con los activos, y como aprovecha lo mejor de estos modelos, ha alcanzado gran importancia y popularidad en los últimos años.
Los sistemas híbridos son muy similares a los sistemas activos, sin embargo, en ellos intervienen elementos pasivos que permiten reducir el consumo energético del sistema ante un sismo. La eficacia de esta cooperación radica en que el control pasivo puede producir la mayor magnitud de reducción de la respuesta mientras que el activo puede proporcionar “el ajuste fino”, es decir es capaz de minimizar aún más los desplazamientos y las aceleraciones de la estructura [64].
Un sistema de control híbrido puede emplear un sistema de control activo para mejorar el desempeño de un sistema de control pasivo, o por el contrario, un sistema de control pasivo se puede utilizar para mejorar las propiedades de respuesta del controlador ante cargas sísmicas y de vientos o disminuir los requerimientos de energía de un sistema activo o semiactivo.
El amortiguador híbrido se ha transformado en el más utilizado de los controladores y con infinidad de aplicaciones. La habilidad del dispositivo para reducir la respuesta estructural radica principalmente en la naturaleza del movimiento de la parte pasiva. Las fuerzas de control del actuador son empleadas para incrementar la eficiencia del HMD e incrementar la robustez a los cambios en las características dinámicas de la estructura.
La energía y fuerzas requeridas para operar un típico HMD son menores que las que necesita un dispositivo activo, cuando ambos tienen comportamiento comparable. La masa amortiguadora pasiva es responsable de la mayor parte de la fuerza de control, mientras que el actuador activo sirve para aumentar la robustez del sistema de control total, permitiendo un mejor control por el aumento de frecuencias de excitación (Nagashima et al., 2001).
Maebayashi et al. [66] proponen un prototipo de HMD para mejorar la respuesta de un edificio sometido a fuertes vientos y sismos moderados. Fujita [34] aplicó un HMD con actuador hidráulico en edificios de gran altura. Nagashima et al. [74] aplicaron un HMD en un edificio de 36 pisos. Saito et al. [90] desarrollaron un HMD a escala real para reducir la respuesta de los edificios ante fuertes vientos y sismos de mediana intensidad. Ávila y Goncalves [4] aplicaron el control híbrido para mitigar las vibraciones en edificios altos causados por fuertes impactos.
Zhou at el. [118] presentaron el análisis y diseño de un amortiguador híbrido original para la repotenciación del Canton Tower, torre de TV en Guangzhou, China, ante mayores cargas de viento debido a los tifones. Li y Cao [60] emplean el HMD en edificios sometidos a sismos y utilizan los algoritmos genéticos para encontrar los parámetros óptimos del modelo. Preumont et al. [84] analizaron el HMD matemáticamente elaborando un ejemplo práctico. Demetriou et al. [26] proponen un nuevo HMD para estructuras livianas de acero. Salvi et al. [92] presentaron la optimización del HMD para reducir la respuesta estructural debido a cargas de impacto.
Collete y Chesne [23] diseñaron un HMD para reducir las vibraciones en resonancia de sistemas de múltiples grados de libertad. Bhaiya et al. [10] estudiaron un control sísmico híbrido en edificios utilizando un TMD y un MRD. Mamat et al. [67] presentaron un control sísmico híbrido en estructuras desarrollando un algoritmo llamado Sliding mode controller (SMC).
Por su naturaleza híbrida, este amortiguador permite variadas combinaciones, lo que constituye una de las temáticas de investigación en la actualidad: que amortiguador híbrido obtiene los mejores resultados o que combinación resulta ser la más efectiva para determinado propósito. Cada combinación de amortiguadores resulta en un sistema de ecuaciones simultáneas particular, con soluciones únicas y diferenciadas con respecto a los demás amortiguadores híbridos.
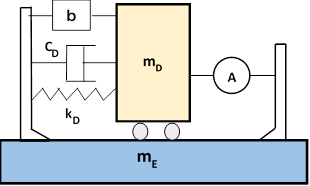
Figura 17 Amortiguador híbrido de masa (TMD Pasivo Inerter + Activo)
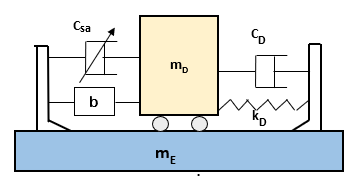
En la figura 18, un amortiguador híbrido, que resulta de la unión de un TMD pasivo y un amortiguador semi activo.
Figura 18 Amortiguador híbrido de masa (TMD Pasivo + Semi Activo)
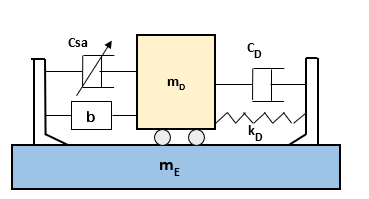
En la figura 19, un amortiguador híbrido, que resulta de la unión de un TMD pasivo inerter y un amortiguador semi activo.
Figura 19 Amortiguador híbrido de masa (TMD Pasivo inerter + Semi Activo)
Spencer y Nagarajaiah [100] presentaron el estado del arte sobre el control estructural, donde incluyen un informe de estructuras con amortiguador de masa híbrido. En la tabla 3 un resumen del informe.
Tabla 3 Estructuras con amortiguadores de masa híbridos (Spencer y Nagarajaiah [100])
8. REFERENCIAS BIBLIOGRÁFICAS
[1] Abé, M. and Igusa, T. (1996). Semi-active dynamic vibration absorbers for controlling transient response. Journal of Sound and Vibration, 198(5), pp.547-569.
[2] Altunişik, A. C., Yetişken, A., and Kahya, V. (2018). Experimental study on control performance of tuned liquid column dampers considering different excitation directions. Mechanical Systems and Signal Processing, 102, 59-71.
[3] Ata, A. A., and Kamel, A. G. (2018). Numerical evaluation of the effect of combined pendulum Tuned Mass Damper on a basic vibrating system. International Journal of Mechatronics and Applied Mechanics, (4), 270.
[4] Avila, S. M. and Goncalves, P. B. (2004). Hybrid control to mitigate excessive vibrations caused by dynamic loading with random perturbations in tall buildings. ABCM Symposium series in Mechatronics, Vol. 1, pp.295-303
[5] Ayorinde, E. O. and Warburton, G. B. (1980). Minimizing structural vibrations with absorbers. Earthquake Engineering and Structural Dynamics, 8, 219–236.
[6] Balendra, T., Wang, C. M. and Cheong, H. F. (1995). Effectiveness of tuned liquid dampers for vibration control of towers. Engineering Structures, 17(9), 668-75.
[7] Balendra, T., Wang, C. and Yan, N. (2001). Control of wind-excited towers by active tuned liquid column damper. Engineering Structures, 23(9), pp.1054-1067.
[8] Barredo, E., Blanco, A., Colín, J., Penagos, V. M., Abúndez, A., Vela, L. G., & Mayén, J. (2018). Closed-form solutions for the optimal design of inerter-based dynamic vibration absorbers. International Journal of Mechanical Sciences, 144, 41-53.
[9] Bathaei, A., Zahrai, S. M. and Ramezani, M. (2017). Semi-active seismic control of an 11-DOF building model with TMD+ MR damper using type-1 and-2 fuzzy algorithms. Journal of Vibration and Control, pp. 1-16
[10] Bhaiya, V., Bharti, S. D., Shrimali, M. K., & Datta, T. K. (2019). Hybrid seismic control of buildings using tuned mass and magnetorheological dampers. Proceedings of the institution of civil engineers-structures and buildings, 1-17.
[11] Bitaraf, M., Ozbulut, O. E., Hurlebaus, S. and Barroso, L. (2010). Application of semi-active control strategies for seismic protection of buildings with MR dampers. Engineering Structures, 32(10).
[12] Borgues Carneiro, R., Moreira Ávila, S. and Vital de Brito, J. (2008). Parametric study on multiple tuned mass dampers using interconnected masses. International Journal of Structural Stability and Dynamics, 8(01), 187-202.
[13] Braz-César, M. T. and Barros, R. (2012). Experimental behaviour and numerical analysis of dampers MR dampers. Fifthteenth world conference on earthquake engineering 15 WCEE, Lisboa.
[14] Brzeski, P., Pavlovskaia, E., Kapitaniak, T. and Perlikowski, P. (2015). The application of inerter in tuned mass absorber. International Journal of Non-Linear Mechanics, 70, 20–29, El Sevier 2015.
[15] Cao, H., Reinhorn, A. and Soong, T. T. (1998). Design of an active mass damper for a tall TV tower in Nanjing, China. Engineering Structures, 20(3), pp.134-143.
[16] Cao, L., & Li, C. (2019). Tuned tandem mass dampers‐inerters with broadband high effectiveness for structures under white noise base excitations. Structural Control and Health Monitoring, 26(4), e2319.
[17] Cetin, H., and Aydin, E. (2019). A New Tuned Mass Damper Design Method based on Transfer Functions. KSCE Journal of Civil Engineering, 23(10), 4463-4480.
[18] Chang, C. C. and Yang, H. (1995). Control of Buildings Using Active Tuned Mass Dampers. Journal of Engineering Mechanics, 121(3), pp.355-366.
[19] Chang, J. C. and Soong, T. T. (1980). Structural control using active tuned mass damper. Journal Engineering Mechanics, ASCE 106, 1091–1098 (1980)
[20] Cheng, F. Y., Jiang, H. and Lou, K. (2008). Smart structures: innovative systems for seismic response control. CRC Press, Taylor and Francis Group.
[21] Chey, M. H., Chase, J. G., Mander, J. B. and Carr, A. J. (2010). Semi-active tuned mass damper building systems: Application. Earthquake Engineering & Structural Dynamics, 39(1), 69-89.
[22] Chung, L. L., Lai, Y. A., Yang, C. S. W., Lien, K. H., & Wu, L. Y. (2013). Semi-active tuned mass dampers with phase control. Journal of Sound and Vibration, 332(15), 3610-3625.
[23] Collette, C., & Chesne, S. (2016). Robust hybrid mass damper. Journal of sound and vibration, 375, 19-27.
[24] Cupich Rodríguez, M. y Elizondo Garza, F. (1998). Amortiguadores magnetoreológicos. Ponencia V Congreso Mexicano de Acústica. Querétaro, México, 17 y 18 de septiembre de 1998.
[25] Datta, T. K. (2003). A state-of-the-art review on active control of structures. ISET Journal of Earthquake Technology, Paper No. 430, Vol. 40, No. 1, pp 1-17.
[26] Demetriou, D., Nikitas, N. and Tsavdaridis, K. (2015). Semi Active Tuned Mass Dampers of Buildings: A Simple Control Option. American Journal of Engineering and Applied Sciences, 8(4), pp.620-632.
[27] Demetriou, D., Nikitas, N. and Tsavdaridis, K. D. (2015). A Novel Hybrid Semi-active Tuned Mass Damper for Lightweight Steel Structural Applications. In Proceedings of the IJSSD Symposium on Progress in Structural Stability and Dynamics, Lisbon, Portugal (pp. 21-24).
[28] Den Hartog, J. P. (1956). Mechanical Vibrations. 4th ed., New York, McGraw-Hill.
[29] Dyke, S. J. (1996). Acceleration Feedback Control Strategies for Active and Semi-active Control Systems: Modeling, Algorithm Development, and Experimental Verification. Ph.D. Dissertation, University of Notre Dame, 1996.
[30] Dyke, S. J., Spencer JR, B. F., Sain, M. K. and Carlson, J. D. (1996). Modeling and control of magnetorheological dampers for seismic response reduction. Smart Materials and Structures 5, pp. 565-575.
[31] Ezeta, J., Mandow, A. y Cerezo, A. (2013). Los Sistemas de Suspensión Activa y Semiactiva: Una Revisión. Revista Iberoamericana de Automática e Informática Industrial RIAI, 10(2), pp.121-132.
[32] Frahm, H., 1911. United States, Patent No. US989958A.
[33] Friedman, A. J. and Dyke, S. J. (2012). Development and experimental validation of a new control strategy considering device dynamics for large-scale MR dampers using real-time hybrid simulation. Technical report, Intelligent Infrastructure Systems Lab Technical Report IISL-003, Purdue University.
[34] Fujita, T. (1994). Application of hybrid mass damper with convertible active and passive modes using hydraulic actuator to high-rise building. In American Control Conference, 1994 (Vol. 1, pp. 1067-1072). IEEE.
[35] Garrido, B. and Serrazin, M. (2017). Effectiveness of Tuned Mass Dampers (TMD) for earthquake protection in chilean buildings. 16th World Conference on Earthquake Engineering 16WCEE, Chile, Paper N° 1077, Registration Code: S- J1464334224, Volume 16.
[36] Ghaboussi, J. and Abdolreza, J. (1995). Active control of structures using neural networks. Journal of Engineering Mechanics, pp 555-567.
[37] Giaralis, A. and Taflanidis, A. A. (2015). Reliability-based design of tuned mass-damper-inerter (TMDI) equipped multi-storey frame buildings under seismic excitation. 12th International Conference on Applications of Statistics and Probability in Civil Engineering ICASP12, Vancouver, Canada, July 12-15, pp. 1-8.
[38] Giaralis, A. and Marian, L. (2016). Use of inerter devices for weight reduction of tuned mass-dampers for seismic protection of multi-storey buildings: the tuned mass damper interter (TMDI). Active and Passive Smart Structures and Integrated Systems, Vol. 9799, 20163.
[39] Giaralis, A. and Petrini, F. (2017). Wind-induced vibration mitigation in tall buildings using the tuned mass damper-inerter (TMDI). Journal of Structural Engineering, ASCE, 2017.
[40] González Padilla, M. A. (2012). Modelado y control PID-difuso de una estructura de edificio sometida a las vibraciones de un temblor. Tesis para optar obtener el grado de Maestra en Ciencias, Especialidad de Control Automático, Centro de investigación y de estudios avanzados del Instituto Politécnico Nacional, unidad Zacatenco, Departamento de control automático, México.
[41] Gutierrez Soto, M. and Adeli, H. (2013). Tuned Mass Dampers. Archives of Computational Methods in Engineering. 20(4), pp.419-431.
[42] Hrovat, D., Barak, P. and Rabins, M. (1983). Semi‐Active versus Passive or Active Tuned Mass Dampers for Structural Control. Journal of Engineering Mechanics, 109(3), pp.691-705.
[43] Hu, Y., Chen, M., Xu, S. and Liu, Y. (2017). Semiactive Inerter and its Application in Adaptive Tuned Vibration Absorbers. IEEE Transactions on Control Systems Technology, 25(1), pp.294-300.
[44] Jansen, L. M. and Dyke, S. J. (2000). Semiactive control strategies for MR dampers: comparative study. Journal of Engineering Mechanics, 126(8), 795-803.
[45] Ji, H. R., Moon, Y. J., Kim, C. H. and Lee, I. W. (2005). Structural vibration control using semiactive tuned mass damper. In The eighteenth KKCNN symposium on civil engineering-KAIST6, Taiwan (pp. 18-20).
[46] Jiang, X. and Hojjat A. (2008), Neuro‐genetic algorithm for non‐linear active control of structures, International Journal for Numerical Methods in Engineering, 75.7, 2008, pp 770-786.
[47] Jiménez, R. E. (2006). Observadores adaptables para edificios con amortiguadores magneto-reológicos. Tesis para obtener el grado de Doctor en ingeniería, Universidad Nacional Autónoma de México, ciudad universitaria, México D.F., 2006.
[48] Kareem, A., Kijewski, T. and Tamura, Y. (1999). Mitigation of motions of tall buildings with specific examples of recent applications. Wind and Structures, 2(3), pp.201-251.
[49] Kaveh, A., Mohammadi, S., O. Khadem, O., Keyhani, A. and Kalatjari, V.R. (2015). Optimum parameters of tuned mass dampers for seismic applications using charged system search. IJST, Transactions of Civil Engineering, Vol. 39, No. C1, pp 21-40, Shiraz University.
[50] Kerboua, M., Benguediab, M., Megnounif, A., Benrahou, K. and Kaoulala, F. (2014). Semi Active Control of Civil Structures, Analytical and Numerical Studies. Physics Procedia, 55, pp.301-306.
[51] Kim, Y. M., You, K. P., You, J. Y., Paek, S. Y., & Nam, B. H. (2016). LQR Control of Along-Wind Responses of a Tall Building using Active Tuned Mass Damper. In World Congress on Advances in Civil, Environmental and Materials Research. ACEM16. Jeju Island, Korea. August 28- Sept. 1
[52] Kitamura, H., Fujita, T., Teramoto, T. and Kihara, H. (1988). Desing and Analysis of a tower structure with a Tuned Mass Damper. Ninth world Conference on earthquake engineering, Tokyo-Kyoto, August 2-9, Vol VIII, 415-420.
[53] Kwok, K. C. S. (1984). Damping Increase in Building with Tuned Mass Damper. Journal of Engineering Mechanics, 110(11), 1645-1649.
[54] Lara, L., Vital de Brito, J. y Valencia, Y. (2012). Reducción de vibraciones en un edificio mediante la utilización de amortiguadores magnetoreológicos. Dyna, año 79, Nro. 171, pp. 205-214.
[55] Lara, L., Valencia, Y. y Vital de Brito, J. (2015). Uso de lógica difusa para la administración de un sistema disipador de energía en estructuras compuesto por amortiguadores magnetoreológicos. Revista Facultad de Ingeniería Universidad de Antioquia, No 74, pp. 151-164.
[56] Lazar, I., Wagg, D. J. and Neild, S. A. (2013). An Inerter vibration isolation system for the control of seismically excited structures. 10th International Conference on Urban Earthquake Engineering, March 1-2, 2013, Tokyo Institute of Technology, Tokyo, Japan.
[57] Lazar, I., Wagg, D. J. and Neild, S. A. (2014). Inerter-based Vibration Suppression Systems for Laterally and Base-Excited Structures. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal, 30 June - 2 July 2014
[58] Lee, M. (2012). Active control to reduce the horizontal seismic response of buildings taking into account the soil-structure interaction. Soil Dynamics and Earthquake Engineering, 42, pp.132-136.
[59] Li, C. and Liu, Y. (2002). Further characteristics for multiple tuned mass dampers. Journal of Structural Engineering, 128(10), 1362-1365.
[60] Li, C. and Cao, B. (2014). Hybrid active tuned mass dampers for structures under the ground acceleration. Structural Control and Health Monitoring, 22(4), pp.757-773.
[61] Li, C., Liu, Y. and Wang, Z. (2003). Active Multiple Tuned Mass Dampers: A New Control Strategy. Journal of Structural Engineering, 129(7), pp.972-977.
[62] Li, C., & Cao, L. (2019). Active tuned tandem mass dampers for seismic structures. Earthquakes and Structures, 17(2), 143-162.
[63] Lin, C. C., Lin, G. L. and Lung, H. Y. (2014). Dynamic test of multiple tuned mass dampers for vibration control of high-rise buildings. Tenth U.S. National Conference on Earthquake Engineering, Frontiers of Earthquake Engineering.
[64] López Almansa, F. and Bozzo, L. M. (2003). Aplicación del control de estructuras al diseño antisísmico. Doctorado en Ingeniería, Universidad de la Coruña, Notas de clase, 2003.
[65] Luft, R. W. (1979). Optimal tuned mass dampers for buildings. Journal of the Structural Division, 105(12), 2766-2772.
[66] Maebayashi, K., Shiba, K., Mita, A. and Inada, Y. (1992). Hybrid mass damper system for response control of building. In Proc. Tenth World Conference on Earthquake Engineering (pp. 2359-64).
[67] Mamat N., Yakub F., Shaikh Salim S.A.Z., Ab Rashid M.Z., Munawarah S., Roslan S.A. (2020) Seismic Control of a Building Structure Equip with Hybrid Mass Damper Using Sliding Mode Control. In: Jamaludin Z., Ali Mokhtar M. (eds) Intelligent Manufacturing and Mechatronics. SympoSIMM 2019. Lecture Notes in Mechanical Engineering. Springer, Singapore
[68] Marian, L., & Giaralis, A. (2014). Optimal design of a novel tuned mass-damper–inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Engineering Mechanics, 38, 156-164.
[69] McNamara, R. J. (1977). Tuned Mass Dampers for Buildings. Journal of the Structural Division, 103(9), 1785-1798.
[70] Matta, E. and De Stefano, A. (2009). Robust design of mass-uncertain rolling-pendulum TMDs for the seismic protection of buildings. Mechanical Systems and Signal Processing, 23(1), 127-147.
[71] Meena, A., Kumar, M., Kumar, A. and Sharma, V. (2016). Vibration control using tuned mass damper. WALIA journal, 32(S2): 33-42
[72] Miller, R. K., Masri, S. F., Dehghanyar, T. J. and Caughey, T. K. (1988). Active vibration control of large civil structures. Journal of Engineering Mechanics, 114(9), 1542-1570.
[73] Morison, J. and Karnopp, D. (1973). Comparison of optimized active and passive vibration absorbers. Joint Automatic Control Conference, No. 11, pp. 932-938.
[74] Nagashima, I., Maseki, R., Asami, Y., Hirai, J. and Abiru, H. (2001). Performance of hybrid mass damper system applied to a 36-storey high-rise building. Earthquake Engineering & Structural Dynamics, 30: 1615–1637. doi:10.1002/eqe.84
[75] Nazarimofrad, E., & Zahrai, S. M. (2016). Seismic control of irregular multistory buildings using active tendons considering soil–structure interaction effect. Soil Dynamics and Earthquake Engineering, 89, 100-115.
[76] Nishimura, I., Kobori, T., Sakamoto, M., Koshika, N., Sasaki, K. and Ohrui, S. (1992). Active tuned mass damper. Smart Materials and Structures, 1(4), pp.306-311.
[77] Nigdeli, S. M., Bekdaş, G. and Sayin, B. (2016). Optimum Tuned Mass Damper Design using Harmony Search with Comparison of Classical Methods, International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2016), AIP Conf. Proc. Vol 1863, 540004-1–540004-4
[78] Nigdeli, S. M., Bekdas, G. and Yang, X. (2016). Optimum Tuning of Mass Dampers for Seismic Structures Using Flower Pollination Algorithm. International Journal of Theoretical and Applied Mechanics, 1, 264-268
[79] Ormondroyd, J. and Den Hartog, J. P. (1928). The theory of dynamic vibration absorber. Journal of Applied Mechanics, Trans. ASME, Vol. 49, pp. A9-A22.
[80] Pastia, C. and Luca, S. G. (2013). Vibration control of a frame structure using semi-active tuned mass damper. Buletinul Institutului Politehnic din lasi. Sectia Constructii, Arhitectura, 59(4), 31.
[81] Peng, G. R., Li, W. H., Du, H., Deng, H. X. and Alici, G. (2014). Modelling and identifying the parameters of a magneto-rheological damper with a force-lag phenomenon. Applied Mathematical Modelling, 38(15), pp. 3763-3773.
[82] Pietrosanti, D., De Angelis, M. and Basili, M. (2017). Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI). Earthquake Engineering & Structural Dynamics, 46(8), pp. 1367-1388.
[83] Pinkaew, T. and Fujino, Y. (2001). Effectiveness of semi-active tuned mass dampers under harmonic excitation. Engineering Structures, 23(7), pp. 850-856.
[84] Preumont, A., Alaluf, D. and Bastaits, R. (2014). Hybrid Mass Damper: A Tutorial Example, Active and passive vibration control of structures, International Centre for Mechanical Sciences CISM, Udine, Italia.
[85] Raveesh R. M. and Sahana T. S. (2015). Effect of Tuned Mass Dampers on Multistore RC Framed Structures. International Journal of Engineering Research & Technology, Vol. 3 Issue 8, ISSN: 2278-0181, pp. 1115-1125.
[86] Ricciardelli, F., Pizzimenti, D. and Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Engineering Structures, 25, 1199–1209.
[87] Radu, A., Lazar, I. F., & Neild, S. A. (2019). Performance‐based seismic design of tuned inerter dampers. Structural Control and Health Monitoring, 26(5), e2346.
[88] Rahmani, H. and Könke, C. (2019). Seismic Control of Tall Buildings Using Distributed Multiple Tuned Mass Dampers. Advances in Civil Engineering, 2019.
[89] Ruiz, R., Taflanidis, A. A., Giaralis, A., & Lopez-Garcia, D. (2018). Risk-informed optimization of the tuned mass-damper-inerter (TMDI) for the seismic protection of multi-storey building structures. Engineering Structures, 177, 836-850.
[90] Saito, T., Shiba, K. and Tamura, K. (2001). Vibration control characteristics of a hybrid mass damper system installed in tall buildings. Earthquake engineering & structural dynamics, 30(11), 1677-1696.
[91] Sakai, F., Takaeda, S. and Tamaki, T. (1989). Tuned liquid column damper - new type device for suppression of building vibrations. Proc. Int. Conf. on Highrise Buildings, Nanjing, China, pp. 926-931.
[92] Salvi, J., Rizzi, E., Rustighi, E. and Ferguson, N. S. (2015). On the optimization of a hybrid tuned mass damper for impulse loading. Smart Materials and Structures, 24(8).
[93] Setareh, M., Ritchey, J., Murray, T., Koo, J. and Ahmadian, M. (2007). Semiactive Tuned Mass Damper for Floor Vibration Control. Journal of Structural Engineering, 133(2), pp.242-250.
[94] Sgobba, S. and Marano, G. C. (2010). Optimum design of linear tuned mass dampers for structures with nonlinear behaviour. Mechanical Systems and Signal Processing, 24(6), 1739-1755.
[95] Smith, M. (2002). Synthesis of Mechanical Networks: The Inerter. proceedings of the 41sl IEEE Conference on Decision and Control, Las Vegas, Nevada, USA, December 2002, pp. 1657-1662.
[96] Soliman, I., Tait, M. and El Damatty, A. (2016). Modeling and analysis of a structure semi-active tuned liquid damper system. Structural Control and Health Monitoring, 24(2).
[97] Sonmez, E., Nagarajaiah, S., Sun, C. and Basu, B. (2016). A study on semi-active Tuned Liquid Column Dampers (sTLCDs) for structural response reduction under random excitations. Journal of Sound and Vibration, 362, pp.1-15.
[98] Spencer, B., Dyke, S. and Sain, M. (1996). Magnetorheological dampers: a new approach to seismic protection of structures. Proceedings of the 35th IEEE Conference on In Decision and Control, Vol. 1, pp. 676-681.
[99] Spencer, B., Dyke, S., Sain, M. and Carlson, J. (1997). Phenomenological Model for Magnetorheological Dampers. Journal of Engineering Mechanics, 123(3), pp.230-238.
[100] Spencer, B. and Nagarajaiah, S. (2003). State of the Art of Structural Control. Journal of Structural Engineering, 129(7), pp.845-856.
[101] Sun, Q., Zhang, L., Zhou, J., and Shi, Q. (2003). Experimental study of the semi‐active control of building structures using the shaking table. Earthquake engineering & structural dynamics, 32(15), 2353-2376.
[102] Symans, M. and Constantinou, M. (1999). Semi-active control systems for seismic protection of structures: a state-of-the-art review. Engineering Structures, 21(6), pp.469-487.
[103] Taflanidis, A. A., Giaralis, A., & Patsialis, D. (2019). Multi-objective optimal design of inerter-based vibration absorbers for earthquake protection of multi-storey building structures. Journal of the Franklin Institute, 356(14), 7754-7784.
[104] Takewaki, I., Murakami, S., Yoshitomi, S. and Tsuji, M. (2012). Fundamental mechanism of earthquake response reduction in building structures with inertial dampers. Structural Control and Health Monitoring, 19(6), 590-608.
[105] Tanaka, N. and Kikushima, Y. (1992). Impact vibration control using a semi-active damper. Journal of Sound and Vibration, 158(2), pp.277-292
[106] Vidal, M. (2008). Análisis y diseño de estructuras con disipadores de energía metálicos en base a criterios de desempeño. Tesis para optar al título de ingeniero civil en obras civiles, Universidad Austral de Chile.
[107] Villareal Castro, G. y Oviedo Sarmiento, R. (2008). Edificaciones con disipadores de energía. libro premio nacional ANR 2008, Lima, Perú.
[108] Wang, J. Y., Ni, Y. Q., Ko, J. M. and Spencer, B. F. (2002). Semi-active TLCDs using magneto-rheological fluids for vibration mitigation of tall buildings. Advances in Building Technology, Volume1, Elsevier Science Ltd., pp. 537-544.
[109] Warburton, G. B. and Ayorinde, E. O. (1980). Optimum absorber parameters for simple systems. Earthquake Engineering & Structural Dynamics, 8(3), 197-217.
[110] Wen, Y., Chen, Z. and Hua, X. (2016). Design and Evaluation of Tuned Inerter-Based Dampers for the Seismic Control of MDOF Structures. Journal of Structural Engineering, ASCE, 2016.
[111] Yalla, S., Kareem, A. and Kantor, J. (2001). Semi-active tuned liquid column dampers for vibration control of structures. Engineering Structures, 23(11), pp.1469-1479.
[112] Yang, G., Spencer, B. F., Carlson, J. D. and Sain, M. K. (2002). Large-scale MR fluid dampers: modeling and dynamic performance considerations. Engineering structures, 24(3), 309-323.
[113] Yazdi, H., Saberi, H., Saberi, H. and Hatami, F. (2016). Designing optimal tuned mass dampers using improved harmony search algorithm. Advances in Structural Engineering, 19(10), pp.1620-1636.
[114] Yoshimura, T., Nakaminami, K., Kurimoto, M. and Hino, J. (1999). Active suspension of passenger cars using linear and fuzzy-logic controls. Control Engineering Practice, 1999, pp 41-47.
[115] Zemp, R., De la Llera, J. C. and Weber, F. (2012). Control of tuned masses using MR dampers and a new real time feedback signal and physical controller. 15 WCEE, Lisboa, 2012.
[116] Zhang, S. Y., Jiang, J. Z. and Neild, S. (2016). Passive vibration suppression using inerters for a multi-storey building structure. In Journal of Physics: Conference Series (Vol. 744, No. 1, p. 012044).
[117] Zhang, Y., Lewis, T. D., Jiang, J. Z., & Neild, S. (2016). Suppression Using Multiple Inerter-based Devices for a Multi-storey Building Structure. In Proceedings of the 6th European Conference on Structural Control (EACS 2016) European Association for the Control of Structures (EACS).
[118] Zhou, F. L., Tan, P., Liu, Y. and Teng, J. (2012). Hybrid mass dampers for anton Tower. CTBUH Journal, (1), 24-29.
[119] Zhou, Z., Najm, H., Vasconez, R., (2016). Effectiveness of Tuned Mass Dampers in Mitigating Earthquake Ground Motions in Low and Medium Rise Buildings. Journal of Engineering and Architecture, Vol. 4, No. 2, pp. 11-22