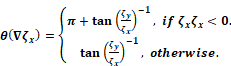A FAST RIGHT
VENTRICLE SEGMENTATION IN CINE-MRI FROM A DENSE HOUGH REPRESENTATION
Jean Alejandro
Pico-Velásquez*1, Alejandra Moreno-Tarazona*2, Luis
Carlos Guayacán-Chaparro*3, Lola Xiomara Bautist-Rozo*4,
Fabio Martínez-Carrillo*5
1Ingeniero de Sistemas. Estudiante UIS. Bucaramanga,
Colombia. jean.pico@saber.uis.edu.co
2Ingeniera de Sistemas. Estudiante UIS. Bucaramanga,
Colombia. alejandra.moreno@saber.uis.edu.co
3Magister en Matemática Aplicada. Estudiante
UIS. Bucaramanga, Colombia. luis.guayacan@saber.uis.edu.co
4Doctora en Ciencias. Docente UIS. Bucaramanga,
Colombia. lxbautis@uis.edu.co
5Doctor en Sistemas y Computación. Docente UIS.
Bucaramanga, Colombia. famarcar@uis.edu.co
*Grupo
de Investigación BIVL2ab, Universidad Industrial de Santander (UIS)
ABSTRACT
Right ventricle (RV) segmentation is essential for the
diagnosis of multiple cardiac pathologies and conditions. However, RV manual
delineation is a tedious task and the design of computational support tools is
challenging due to geometric and dynamic variability. This work introduces a
representation based on the dense Hough transform (DHT) that allows a
non-parametric characterization of the shape, encoding each voxel by its
curvature and orientation. This representation is integrated into a Bayesian
tracking approach, which efficiently segments the RV structure throughout the
cardiac cycle. The proposed approach was evaluated on a public dataset, with 16
patients, achieving a Sørensen-Dice coefficient of 0.87 and 0.92, for complete
volumes and basal structures, respectively. These results evidence an adequate
fit of the proposed model with respect to RV shape throughout the entire
cardiac cycle.
Keywords: Dense Hough Transform; Heart Characterization; RV Segmentation; Heart
Disease Classification; Cardiac MRI.
Recibido: 25 de octubre de 2021. Aceptado: 02
de marzo de 2022
Received: October 25, 2021.
Accepted: March 25, 2022
UNA SEGMENTACIÓN RÁPIDA DEL VENTRÍCULO DERECHO EN
CINE-MRI A PARTIR DE UNA REPRESENTACIÓN DENSA DE HOUGH
RESUMEN
La segmentación del Ventrículo Derecho (VD) es
esencial para el diagnóstico de múltiples patologías y condiciones cardiacas.
Sin embargo, su delineación manual es una tarea tediosa y el soporte
computacional resulta complejo debido a la variabilidad geométrica y dinámica.
Este trabajo introduce una transformación y representación densa de Hough (TH)
que permite una caracterización no paramétrica de la forma, codificando cada
vóxel por su curvatura y orientación. Esta representación es integrada en un
enfoque de seguimiento bayesiano, que logra de forma eficiente segmentar la
estructura del VD, a lo largo del ciclo cardíaco. El enfoque propuesto fue
evaluado en un conjunto de datos públicos, con 16 pacientes, logrando un
coeficiente Sørensen-Dice de 0,87 y 0,92, para volúmenes completos y
estructuras basales, respectivamente. Estos resultados evidencian una adecuada
adaptación del modelo propuesto respecto a la forma del VD a lo largo de todo
el ciclo cardíaco.
Palabras
clave: Transformada densa de Hough;
Caracterización del corazón; Segmentación del VD; Clasificación de enfermedades
cardiacas; Secuencias cardiacas MRI.
Como citar este artículo: Pico-Velásquez, J., A., Moreno-Tarazona,
A., Guayacán-Chaparro, L., C., Bautist-Rozo, L., X., & Martínez-Carrillo,
F. (2022). A fast right ventricle segmentation in cine-mri from a dense hough
representation, 18(35), 84-97. https://doi.org/10.33571/rpolitec.v18n35a6
1.
INTRODUCTION
Cardiovascular diseases (CVDs) are
the main cause of death around the world, according to the World Health
Organization (WHO). About 17.9 million people die each year from CVDs,
corresponding to 31% of all deaths worldwide [1]. The analysis of the
structural and dynamic patterns of the heart is crucial to evaluate its
functionality, supporting the diagnosis and prognosis of associated diseases.
Currently, characterization of the right ventricle (RV) has proven to be one of
the main ways to analyze these spatio-temporal patterns and support diagnostic
decisions [2,3,4]. For instance, volumetric RV patterns support the
characterization of pulmonary hypertension, cardiomyopathy, myocardial
infarction, and congenital heart diseases [5,6,7]. However, the first step to
assess RV is the contour delineation task, which is a tedious expert-dependent
task that introduce inter and intra-observer variability [8]. Additionally,
during the clinical routine, the RV delineation could take more than 15 minutes
for each patient [4].
Hence, computational tools are required
to automatically delineate RV structures and efficiently support clinical
procedures [9]. This is a challenging task because of the high dynamic and
structural variability of RV. Additionally, the low resolution of cine-MRI
acquisitions difficult to track non-linear cardiac dynamics. Moreover,
trabecular muscles, are not well separated from the RV wall [10]. In fact, in
almost all studies, RV delineation is only performed during end-diastole and
end-systole, that is, when the greatest relaxation or contraction of the
ventricular cavities occurs, losing information about global structural changes
during time.
In the literature, global
segmentation strategies have been mainly applied to delineate the RV, exploring
from different statistical shape models that involve likelihood appearance
measures [8,11]. In these approaches, a set of manual delineations built a
statistical model that is matched over a new cine-MRI according to some
predefined rules on image space. These approaches achieved a proper global matching
but lacked local shape definition due to the high RV variability across
different spatial and temporal slices, as well as the variability among
patients. Additionally, atlas-based strategies index a set of training samples
with associated delineations that are individually mapped to the new cine-MRI,
using registration techniques. In such a case, the delineation of an atlas
image with minimal transformation w.r.t the new volume is set as a new
segmentation. These approaches overcome noise and low tissue-to-blood contrast
problems but namely report several limitations regarding the adaptation of
local template details [12,13].
These alternatives use prior
anatomical information to guide the segmentation process. For instance, Petit
Jean et al. [4] proposed an automatic segmentation method based on multi-label
graph cuts, which makes use of a probabilistic shape model. First, atlas
examples are non-rigid registered with respect to unknown images. Then, a
probabilistic model based on the registered images is created and a shape model
is obtained by merging several atlases after their non-rigid registration on
the unknown image. Finally, this prior is incorporated into the multi-label
graph cut framework in order to guide the segmentation. The main advantage of
this method is the low computational cost. Nevertheless, the performance and
results of this methodology mainly depends on the method used for the non-rigid
registration.
Likewise, machine learning
approaches have been proposed to carry out RV segmentation. Particularly,
convolutional neural networks (CNNs) have achieved record-breaking accuracy
performances. For instance, Zhen et al. [14] proposed a directed bi-ventricular
volume prediction method based on CNNs and random forests. Their method takes
advantage of both, unsupervised representation learning and supervised volume
estimation. Avendi et al. [15] proposed a method based on CNN and a stacked
autoencoder, which is trained to locate the region of interest (RoI) and
delineate efficiently the boundary of RV. Although these methods obtain
remarkable results and they have the ability to perform transfer learning, CNNs
based approaches require a considerable amount of data for training and are
highly dependent on the implemented architecture.
The main contribution of this work
is a robust and fast Hough representation that follows, captures and delineates
the complex RV shape along the cardiac cycle. The method starts by matching an
average template over the initial frame of the cine-MRI. Such template allows
us to coarsely localize and define the structure of the RV and the surrounding
regions, i.e., the background. Hence, a dense Hough transform (DHT) codes
ventricle information from local curvature and orientation into the region of
interest. These primitives are accumulated in representation tables (R-Tables)
to follow the structure along time and considering non-parametric shapes. From
that region of interest, a spatial and motion deformation model is described as
a recursive Bayesian strategy. The DHT is also back-projected to define a
coarse RV segmentation that complements and updates the appearance observation
model.
2.
MATERIALS AND METHODS
The structure and function of the
right ventricle play an essential role in the diagnosis and monitoring of many
cardiovascular diseases. However, the complex RV dynamic and its non-parametric
shape make difficult the segmentation process. In this work is introduced a
low-level heart representation using a temporal Bayesian framework through a multi-scale
DHT. This transformation is operated pixel-wise into a multi-scale scheme that
allows following non-parametric shapes along time. From such local
representation, it is possible to characterize cardiac structures that exhibit
complex spatial and temporal patterns. Then a probabilistic model is
implemented to segment RV from the background. At each time, the DHT and
probabilistic model are complemented and updated to achieve a temporal
segmentation. The following subsection describes in detail the steps of the
proposed RV segmentation.
2.1. RoI estimation: rigid training initialization: First,
a set of new cine-MRI training sequences is rigidly registered as an
atlas-based approach. Then, the initial localized RoI (Ω), is herein used to
learn an RV template 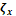 to avoid undesired deformations of its morphology,
following a dense per-voxel Hough representation. This template
to avoid undesired deformations of its morphology,
following a dense per-voxel Hough representation. This template 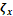 is modeled over each RV heart contour given by a
physician expert. Finally, the non-rectangular RoI (Ω) is estimated according
to a transformed contours average of samples, i.e.,
is modeled over each RV heart contour given by a
physician expert. Finally, the non-rectangular RoI (Ω) is estimated according
to a transformed contours average of samples, i.e., 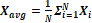 where
where 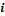 corresponds to each sample of a training sequence.
In Figure 1 is illustrated the process of rigid registration of a set of
training samples w.r.t a target. The initial delineation, taken from the
average, is then characterized with the DHT and evolved according to a
statistical framework.
corresponds to each sample of a training sequence.
In Figure 1 is illustrated the process of rigid registration of a set of
training samples w.r.t a target. The initial delineation, taken from the
average, is then characterized with the DHT and evolved according to a
statistical framework.
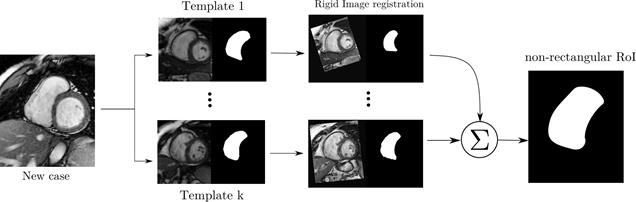
Figure 1: Automatic non-rectangular RoI
estimation. First, the dataset volumes are rigidly registered w.r.t the target
(New case). Then, all contours are transformed to fit the target. Finally, an
average between all contours is computed to obtain a non-rectangular RoI
estimation Ω for the new case.
2.2. Dense Hough Transform for heart
characterization: In this work is implemented a DHT
to capture local heart information by coding curvature and orientation at voxel
level. Such characterization is carried out in both: space and time allowing a
non-parametric characterization of cardiac structures. Also, this work involves
multi-scale evaluation of cardiovascular magnetic resonance (CMR) imaging
sequences, as well as analysis of motion primitives and deformations that can
be coded in cumulative tables to achieve a robust representation. The heart
structures were coded from DHT and used in right ventricle segmentation (see
Figure 2).
Firstly, a cine-MRI captures the
heart structures together with surrounding organs along the cardiac cycle. A
fundamental task is to obtain a representation of the cardiac structures over
time, allowing to identify and localize these regions automatically from others
in the cine-MRI. An initial delineation of cardiac structures made by an expert
cardiac radiologist is taken at the first slice. Then a Dense Hough
representation allows to detect and follow the marked regions of interest
(RoIs). For doing so, a template 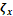 is computed over a rectangle surrounding RoIs,
centered at position
is computed over a rectangle surrounding RoIs,
centered at position 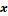 . Since an MRI sequence is a temporal volume, such a template
can be computed at every slice where cardiac structure exists or can be
computed at independent relevant slices for the analysis (e.g., the basal, mid
and apical slices). The characterized template is then used to search and
detect the respective RoIs in the whole slice for all cine-MRI volumes.
. Since an MRI sequence is a temporal volume, such a template
can be computed at every slice where cardiac structure exists or can be
computed at independent relevant slices for the analysis (e.g., the basal, mid
and apical slices). The characterized template is then used to search and
detect the respective RoIs in the whole slice for all cine-MRI volumes.
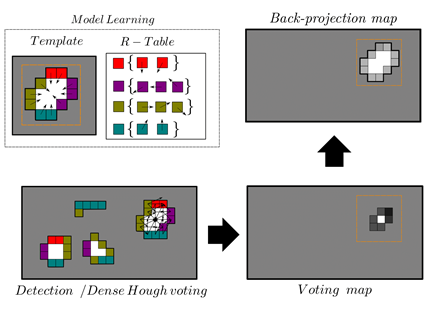
Figure 2: Automatic RV segmentation using
DHT. The DHT allows to detect and follow a region that bound the right
ventricle. Firstly, some features of a template are calculated at the pixel
level and stored together with the distance from each pixel to the center of
the template. Then, the same process is performed on each frame extracting the
same features. Then, a search in the R-table is performed to obtain the
position in which each vote is going to take place. Finally, a back-projection
process is performed to recover the pixels that contributed the most in the
estimation of the center.
2.2.1 Learning - 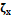 representation: Let be
representation: Let be 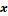 a pixel location with coordinates
a pixel location with coordinates 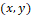 . The template is characterized using a
multi-scale framework
. The template is characterized using a
multi-scale framework 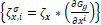 that essentially exploits the spatial
structure and features provided by the first and second derivatives at
different scales
that essentially exploits the spatial
structure and features provided by the first and second derivatives at
different scales 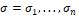 . This multi-scale approach probed to
reduce the influence of spurious structures (e.g., the left ventricle),
improving detection [16]. From such template
. This multi-scale approach probed to
reduce the influence of spurious structures (e.g., the left ventricle),
improving detection [16]. From such template 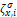 is possible to compute local primitives
at each location
is possible to compute local primitives
at each location 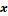 such as the curvature
such as the curvature 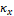 and gradient orientation
and gradient orientation 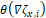 [16].
[16].
3.
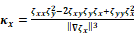 (1)
(1)
4.
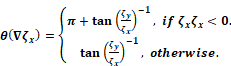 (2)
(2)
From such multi-scale representation, it is
possible to perform a more robust search in the next frames to detect the
cardiac structures of interest. To do so, two representation tables (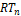 ) were defined as accumulators’ arrays that
count occurrences of gradient orientation (
) were defined as accumulators’ arrays that
count occurrences of gradient orientation (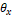 ) and curvature (
) and curvature (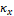 ) for each pixel, respectively. To limit
the size, these features are quantified, and the curvature is bounded to
[-1,1]. For R-Tables calculation, those sets of pixels with a gradient
magnitude equal to zero are not considered, avoiding non defined value
estimations. The algorithm 1 shows systematic construction of the two R-tables.
In such case
) for each pixel, respectively. To limit
the size, these features are quantified, and the curvature is bounded to
[-1,1]. For R-Tables calculation, those sets of pixels with a gradient
magnitude equal to zero are not considered, avoiding non defined value
estimations. The algorithm 1 shows systematic construction of the two R-tables.
In such case 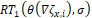 concatenates weighted gradient
orientations and relative positions
concatenates weighted gradient
orientations and relative positions 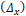 w.r.t the center.
w.r.t the center. 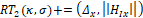 concatenates information with respect to
the curvature index by the Frobenius norm of the Hessian matrix.
concatenates information with respect to
the curvature index by the Frobenius norm of the Hessian matrix.

Figure 3 illustrates the characterization
process for a cardiac structure of interest, e.g., the RV. In this case, all
pixels inside the rectangular RoI constitute the template for learning. This
process is done once for each MRI volume. These RTs are updated by adding the
RV structural changes over time.

Figure 3: Basal slice: RV characterization
example using a rectangular RoI 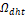 as an input of DHT, these RTs are
updated by adding the RV structural changes over time depending on
as an input of DHT, these RTs are
updated by adding the RV structural changes over time depending on 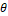 ,
, 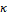 and
and 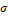 .
.
2.2.2.
Detection - searching 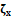 :
From such local RoI characterization it is possible to detect arbitrary
non-analytical tissues such as the heart ventricles. Each
:
From such local RoI characterization it is possible to detect arbitrary
non-analytical tissues such as the heart ventricles. Each 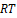 is
then projected into each new slice to search for similar features and build an
accumulation map (𝚪).
Every pixel vote, according to its orientation and curvature indexes and its
votes, are weighted as indicated in the
is
then projected into each new slice to search for similar features and build an
accumulation map (𝚪).
Every pixel vote, according to its orientation and curvature indexes and its
votes, are weighted as indicated in the 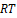 .
The local maximum in 𝚪
is then considered as the center of the detected RoI. Algorithm 2 summarizes
the automatic detection of RoIs for every slice at each cine-MRI of the
dataset.
.
The local maximum in 𝚪
is then considered as the center of the detected RoI. Algorithm 2 summarizes
the automatic detection of RoIs for every slice at each cine-MRI of the
dataset.
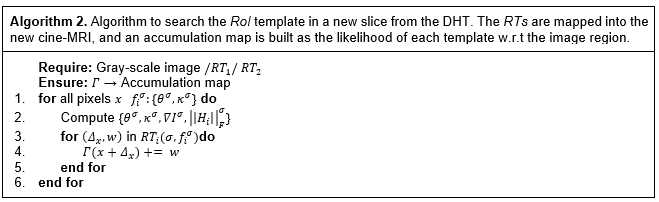
Figure 4 shows the accumulation map
computed for each frame and each slice of the Cine-MRI sequence. Where the
brightest pixel at position 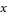 represents the RV center with some margin
of error.
represents the RV center with some margin
of error.
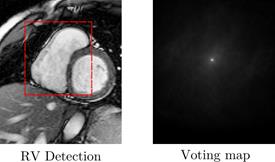
Figure 4: Left: RV RoI detected for a Basal
slice. Right: Accumulation map which represents the voting process for
detection.
1.
2.
2.1.
2.2.
2.2.1.
2.2.2.
2.2.3.
Back-projection: From
the voting map, it is possible to recover the center of the estimated RoI 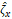 along the cardiac MRI sequence. Then, at each time it is possible to obtain an
automatic identification of the selected structure. The pixels that better
represent cardiac structures have significant contributions to the voting map.
From such an assumption, a non-parametric shape can be recovered from the
voting map by selecting the pixels according to each contribution [17]. In the
segmentation scenario, a back-projection strategy is implemented from a
thresholded version of contributing pixels. This coarse model is used to update
the segmentation model that leads to better discrimination of foreground and
background pixels into the region of interest.
along the cardiac MRI sequence. Then, at each time it is possible to obtain an
automatic identification of the selected structure. The pixels that better
represent cardiac structures have significant contributions to the voting map.
From such an assumption, a non-parametric shape can be recovered from the
voting map by selecting the pixels according to each contribution [17]. In the
segmentation scenario, a back-projection strategy is implemented from a
thresholded version of contributing pixels. This coarse model is used to update
the segmentation model that leads to better discrimination of foreground and
background pixels into the region of interest.
2.3. Bayesian Segmentation Model: Once the Hough representation is
recovered, the main scenario for evaluation is heart chambers segmentation. For
doing so, a probabilistic approach is herein implemented with the Hough
transformation. The heart shape estimation 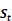 is involved in a well-defined cardiac cycle description
is involved in a well-defined cardiac cycle description 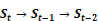 …, where consecutive shape changes depend on temporal motion and
deformation history. Additionally, to history information, at each time
…, where consecutive shape changes depend on temporal motion and
deformation history. Additionally, to history information, at each time 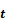 , it is possible to recover a particular observation of the heart
, it is possible to recover a particular observation of the heart 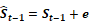 , where
, where  represent noise in the captured measurements. From such analysis,
we can approximate the heart dynamic segmentation as a Bayesian inference of
first order, described by Chapman-Kolmogórov equation:
represent noise in the captured measurements. From such analysis,
we can approximate the heart dynamic segmentation as a Bayesian inference of
first order, described by Chapman-Kolmogórov equation:
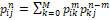 (3)
(3)
Where 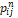 represents the transition probability from
state
represents the transition probability from
state 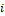 to state
to state 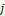 in
in 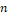 steps or iterations. For our case, we
assume that heart chambers do not change their shape between frames abruptly.
In this assumption, we consider a Markovian first approximation, i.e.,
the most important information of motion history is in the previous frame (
steps or iterations. For our case, we
assume that heart chambers do not change their shape between frames abruptly.
In this assumption, we consider a Markovian first approximation, i.e.,
the most important information of motion history is in the previous frame (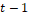 ). Like in [17], a segmentation model is
adopted which is trained and updated during the cardiac cycle to improve
discrimination. For this segmentation model, a recursive Bayesian formulation
approach is used, based on tissue-to-blood contrast present in the RoI in a
time
). Like in [17], a segmentation model is
adopted which is trained and updated during the cardiac cycle to improve
discrimination. For this segmentation model, a recursive Bayesian formulation
approach is used, based on tissue-to-blood contrast present in the RoI in a
time  . The Bayesian inference allows to increase
model robustness by incorporating the information present in previous sequences
(
. The Bayesian inference allows to increase
model robustness by incorporating the information present in previous sequences
(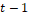 ).
To create this model, two probabilities are defined for each position
).
To create this model, two probabilities are defined for each position 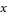 , that is, probability of the pixel
, that is, probability of the pixel 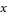 to belong to RV (Foreground) and
probability of the pixel
to belong to RV (Foreground) and
probability of the pixel 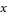 to be any other tissue (Background). Let
to be any other tissue (Background). Let 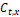 be the pixel class at the position
be the pixel class at the position 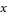 at a time
at a time  , where
, where 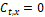 for surrounding tissues and
for surrounding tissues and 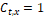 for RV. Furthermore, be
for RV. Furthermore, be 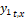 the tissue-to-blood contrast information
in the position
the tissue-to-blood contrast information
in the position 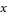 . The probability of the pixel
. The probability of the pixel 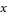 pertaining to the right ventricle
pertaining to the right ventricle 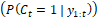 is defined by:
is defined by:
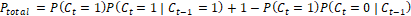
(4)
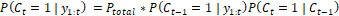
Let 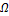 be the RoI obtained in Figure 1. From
be the RoI obtained in Figure 1. From 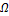 , two scaled versions are created (
, two scaled versions are created (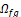 ,
,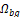 ). For the first case
). For the first case 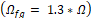 the inner region is taken, which contains
the pixels corresponding to the RV. In the second case, the region resulting
from the difference between
the inner region is taken, which contains
the pixels corresponding to the RV. In the second case, the region resulting
from the difference between 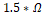 and
and 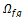 , i.e.,
, i.e., 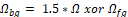 is taken. Once
is taken. Once 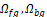 are obtained, color histograms are
calculated into these regions, which are normalized and quantified to 12 and 24
bins per region. These histograms contain the tissue-to-blood contrast
information necessary for the construction of the model based on Bayesian
inference. A prior
are obtained, color histograms are
calculated into these regions, which are normalized and quantified to 12 and 24
bins per region. These histograms contain the tissue-to-blood contrast
information necessary for the construction of the model based on Bayesian
inference. A prior 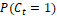 is initialized in
is initialized in 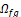 . The resulting
. The resulting 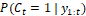 can be seen in Figure 5-(a)(c). Thus, the
final segmentation is obtained by thresholding this RV probability image (see
Figure 5-(b)(d)).
can be seen in Figure 5-(a)(c). Thus, the
final segmentation is obtained by thresholding this RV probability image (see
Figure 5-(b)(d)).
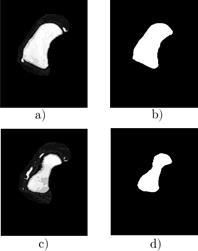
Figure 5: Segmentation model. a) Diastole RV
probability; b) Diastole segmentation; c) Systole RV probability; d) Systole
segmentation.
The segmentation and Dense Hough (DH)
detection models are updated in a complementary manner, i.e., the upgrading of
one model depends on the other. The DH model update recalculates the 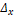 displacements within the rectangular RoI
displacements within the rectangular RoI 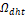 (Figure 3). In such a case, the weights
are then updated using the constraints shown in the equations below. Where if
the
(Figure 3). In such a case, the weights
are then updated using the constraints shown in the equations below. Where if
the 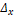 displacements exist in the
displacements exist in the 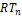 model their weight will be updated,
otherwise, this displacement will be added to the corresponding
model their weight will be updated,
otherwise, this displacement will be added to the corresponding 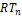 .
.
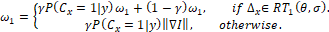
(5)
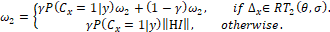
As RV has several deformations during the
MRI sequence, the Hough descriptor should take into account these changes. In
Figure 6-(c)(d) is shown how the detection works for a critical scene where the
RV has the maximum contraction (end-systole). It is noticeable how the voting
map becomes noisier but still detects the RV correctly. In this case, the model
was trained for the diastole scenario.
The segmentation model updating uses
back-projection map information to update the histograms for RV and non-RV
tissues. To do so, only pixels with vital importance or significant influence
in the voting map are taken into account; in our case, only greater than 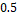 (in a range from 0 to 1). These pixels
increase their importance in the probability model, while the others decrease
(as shown in the equation below), turning into a better discrimination.
Empirically an update factor
(in a range from 0 to 1). These pixels
increase their importance in the probability model, while the others decrease
(as shown in the equation below), turning into a better discrimination.
Empirically an update factor 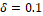 was chosen.
was chosen.
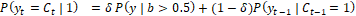 (6)
(6)
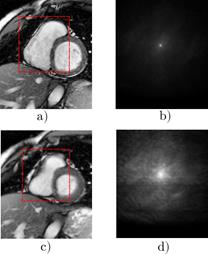
Figure 6: Hough model updating. a) Diastole
cine-MRI; b) Diastole voting map; c) Systole cine-MRI; d) Systole voting map.
5.
6.
6.1.
6.2.
6.3.
2.4 Experimental results: The evaluation of the proposed method was
performed over the Right Ventricle Segmentation Challenge (RVSC) dataset which
was organized by MICCAI'12 [4]. This consists of a total of 16 patient
short-axis volumes and a set of ground truth contours. All patient data were
anonymized according to the MICCAI'09 LV segmentation challenge criteria. The
CMR study was performed at 1.5T Symphony Tim, Siemens Medical Systems. A
conventional 2-chamber view was acquired with a total of 10-14 short-axis
slices from Apex to Basal. The examination parameters were the following: TR =
50 ms; TE = 1.7ms; flip angle = 55˚; slice thickness = 7 mm; matrix size = 256
× 216; Field of view (FOV) = 360 mm × 420 mm; 20 images per cardiac cycle.
Manual delineation was carried out by an expert cardiologist who manually
delineated endocardial and epicardial contours of the RV.
As suggested by dataset authors, two different metrics were
herein used to evaluate the performance of the proposed approach: The global
Sørensen-Dice coefficient (DSC) and the local Hausdorff Distance (HD). On the
one hand, the similarity DSC computes the spatial overlap between two
discretely labeled objects. It is a traditional metric for segmentation
performance evaluation, where the similarity between the ground truth (GT) and
the RV segmentation is measure in a range from 0 to 1 (higher is better),
described as 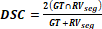 . On the other hand, the HD measures how far two contours are from each
other. This metric gives us complementary information of similarity between A
and B. Defined as:
. On the other hand, the HD measures how far two contours are from each
other. This metric gives us complementary information of similarity between A
and B. Defined as: 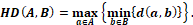
3.
EVALUATION AND RESULTS
Firstly, a
qualitative evaluation of obtained RV segmentation is illustrated in Figure 7
and Figure 8. In such cardiac cine-MR short-axis images can be observed the
performance of the proposed strategy in basal heart regions, being close to
expert manual delineations. Also, for different shapes, the strategy is well
adapted during the cardiac cycle (Figure 7). The approach can follow and
tracking the RV motion and deformation. For apical images, the segmentation
represents a greater challenge because of the small regions where the RV RoI is
present (Figure 8 - second row). Even for an expert physician, these slices are
a tough task. Nevertheless, the proposed approach achieves an appropriate
segmentation in these apical regions with some local limitations.
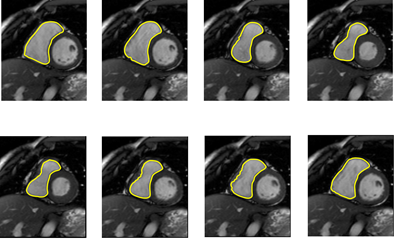
Figure 7: Segmentation results for patient
#4 during cardiac cycle. Yellow: proposed RV segmentation.
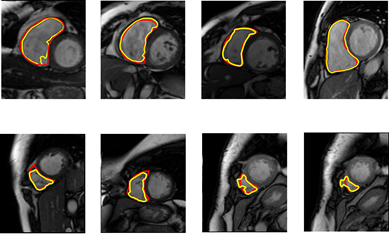
Figure 8: Segmentation results from Basal
to Apex. Yellow: proposed RV segmentation; Red: ground truth contour.
Secondly, an exploration was carried out to adjust the
proposed approach w.r.t to parameters that are sensitive to the segmentation.
The selected parameters evaluated in a spectrum of values are: non-rectangular
RoI threshold, non-rectangular RoI scaling factor, color histogram bins, and
segmentation threshold, described as follows.
a) b)
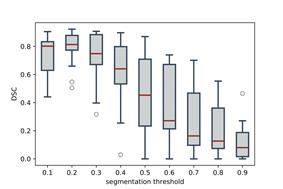
c) d)
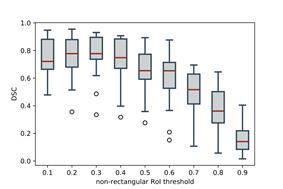
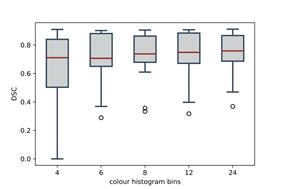
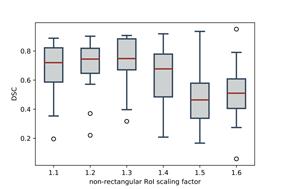
Figure 9: Methodology parameters influence
in DSC performance. a) Non-rectangular RoI threshold parameter. b) Color
histogram bins parameter. c) Non-rectangular RoI scaling factor parameter. d)
Segmentation threshold parameter. Parameters (b), (c) and (d) correspond to the
segmentation model.
·
Non-rectangular
RoI threshold: This procedure is applied to the average
image contour obtained from the rigid registration. The threshold values are
fixed in an interval [0-1]. For values close to zero, a significant area of common
delineations is taken into account, while for values close to one, only common
values in whole delineations are considered. In Figure 9-a), a value of 0.3
yields the best performance and less data variability, with an average accuracy
of 0.81. In such a case, the proposed approach is better when it is possible to
admit a larger region to initialize the algorithm.
● Non-rectangular RoI scaling factor (FG/BG): to define the size of foreground (FG) and
background (BG) area sizes, a RoI scaling factor is computed following the
relation 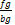 (see Figure 10). As illustrated in Figure
9-(c), the best result is obtained when the foreground RoI scale is 1.2 times
bigger than the background. Statistically, such fact has sense since both
regions are well balanced regarding samples to compute the histograms of each
region.
(see Figure 10). As illustrated in Figure
9-(c), the best result is obtained when the foreground RoI scale is 1.2 times
bigger than the background. Statistically, such fact has sense since both
regions are well balanced regarding samples to compute the histograms of each
region.
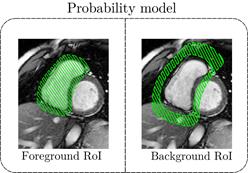
Figure 10: Left: Area  where the RV histogram is calculated;
Right: Area
where the RV histogram is calculated;
Right: Area 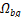 where the surrounding tissue histogram is
calculated.
where the surrounding tissue histogram is
calculated.
● Color histogram bins: For the quantization process, necessary to
build the tissue-to-blood contrast probability model. Specifically, 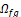 and
and 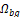 represent histograms quantization. In
Figure 9-(b) is shown that the performance remains almost constant for a
different number of bins.
represent histograms quantization. In
Figure 9-(b) is shown that the performance remains almost constant for a
different number of bins.
● Segmentation threshold: This is the final step for segmentation,
which selects a set of pixels likely belonging to RV according to its
probability of being RV. All pixels below the segmentation threshold are
considered surrounding tissue. As expected, lower thresholds allow to take
major information of the RV area, leading to better performance of the proposed
approach. Being the best performance value 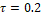 , as shown in Figure 9-(d).
, as shown in Figure 9-(d).
In a third evaluation, the proposed
approach was tested with three different configurations by coding different
input delineations. The result of these three different configurations is shown
in Table 1. In the first case only one rectangular region was passed without
any prior information of the heart shape (Fully rectangular). Interestingly,
the proposed approach achieves in average an 88% of accuracy for basal slices,
discovering the true shape of the ventricle automatically by only using
appearance information.
A second approximation takes into account
the information from an initial delineation by computing the DHT overall
region. As expected, the result is considerably better with an accuracy of 90%
due to the initial consideration of shape. Finally, the best result is achieved
when the segmentation model is also updated w.r.t to the information of DHT at
each time, i.e., during the cardiac cycle, achieving an accuracy of 92% in
average of basal slices and 87% in all cardiac slices. Therefore, the model
combines rectangular regions for detection and non-parametric regions for
segmentation and updating. It is worth noting the improvement in apical slices
by introducing properly prior knowledge of the training delineations.
Table 1. Quantitative comparison results
for different RoIs approaches. Rectangular + Non-Rectangular V1 represents a
computation of the DHT overall region, meanwhile Rectangular + Non-Rectangular
V2 represents the information obtained with the DHT during the cardiac cycle.
|
RoI
Approach
|
Basal
|
All slices
|
|
Full Rectangular
|
0.88
|
0.66
|
|
Rectangular + Non-Rectangular V1
|
0.90
|
0.76
|
|
Rectangular
+ Non-Rectangular V2
|
0.92
|
0.87
|
In Table 2 is summarized the Dice
Similarity Coefficient (DSC) and Hausdorff Distance (HD) obtained by the
proposed approach. A leave-one-out cross-validation was performed. For this, a
total of 16 patients with contours from the RVSC dataset were used. The results
were split for basal and all slices (basal, mid, and apex). The best DSC was
for basal slices being around 0.92 on average with a low standard deviation.
Both DSC and HD show a very compact performance of the obtained segmentation in
global terms as well as the local description of RV shape. Nevertheless, the
DSC decreases by around 0.1 from basal to apex. In the state-of-the-art, most
methods report DSC over 0.9 [18,19,20] for basal slices. Additionally, adding
apical slices decreases the DSC performance around 0.7. This indicates that
increasing the segmentation performance for apical slices is a step forward.
Most of the methods in the literature present problems with apex segmentation
due to their appearance in MRI images, so creating models that do not rely
fully on appearance for apical slices may improve the results. The segmentation
error for apical slices is not considered a limiting factor for volume
calculation. However, it can be critical for other types of applications and
studies. Considering the inter-expert variability of 0.90 ± 0.10 [4], our
methodology constitutes a potential tool to support automatic RV segmentation.
Table 2. RV Segmentation results; DSC ±
standard deviation. Average HD in pixels.
|
|
Measures
|
|
|
DSC (mean)
|
HD (mean)
|
|
Basal
|
0.92±0.05
|
4.19±1.54
|
|
All slices
|
0.87±0.12
|
4.20±1.41
|
Finally, in Table 3, the DSC obtained in
our proposed method was compared with the best results obtained in the RVSC at
MICCAI'12 [4]. These methods use different approaches, such as 4D watershed
graph-cut segmentation [21], 2D multi-atlas registration [22], 3D multi-atlas
registration [23] and 2D shape prior graph-cut segmentation [24]. Some of these
methods need user inputs, i.e., are semi-automatic. For instance, O. Maier et
al. [21] needs rough contouring of four to five 2D slices. The highest
quantitative result of semi-automatic methods was the BIT-UPM, which reached a
DSC of 0.80, while the best of the automatic methods (CMIC) reached 0.78.
Compared to these state-of-art methodologies, our method works automatically by
non-rigid registering atlases w.r.t an unknown MRI sequence (input) and, after
a non-rectangular RoI detection, a probabilistic appearance model is applied to
finally obtain an accurate segmentation achieving a DSC of 0.87.
Table 3. Comparison of Dice Score with best
methods presented in the RVSC MICCAI 2012. All slices are considered.
|
RoI Approach
|
Basal
|
All slices
|
|
Proposed approach
|
Automatic
|
0.87±0.12
|
|
CMIC (M.
Zuluaga et al.)
|
Automatic
|
0.78±0.23
|
|
SBIA (Y. Ou
et al.)
|
Automatic
|
0.55±0.32
|
|
BIT-UPM (O. Maier et al.)
|
Semi-automatic
|
0.80±0.19
|
|
ICL (W. Bai
et al.)
|
Semi-automatic
|
0.78±0.20
|
|
LITIS (D. Grosgeorge et al.)
|
Semi-automatic
|
0.76±0.20
|
4.
DISCUSSION
This work
introduced a method for RV segmentation from cardiac cine-MRI sequences by
integrating spatio-temporal information into a compact DHT descriptor and a
probabilistic model. RV spatial and motion deformation was herein modeled as a
dense representation achieved by a DHT and a recursive probabilistic Bayesian
model. An average template was firstly rigid registered to the new cardiac MRI
sample as initial heart region estimation. The observations into the
probabilistic model were defined as RV and background appearance
representations. Complementary to the observations, a non-parametric shape
characterization was defined as the result of a DHT, that allows to globally
track the RV and locally update the appearance model. The DHT codes curvature
and orientation at voxel level and follows non-linear changes on RV shape. The
proposed approach was evaluated over the RVSC dataset, which includes a total
of 16 patients. Also was evaluated in terms of the DSC for complete volumes and
only basal RV structures, achieving rates of 0.87 and 0.92, respectively. These
results outperformed the state-of-the-art methods, with the main advantage of
the flexibility and independence of large training datasets. Additionally, this
work was able to obtain RV segmentations along the cardiac cycle, without using
any additional prior delineations.
Some of the
RVSC works make use of different approaches, such as Atlas-based, shape
prior-based, and prior-based methods (Table 3). In general, multi-atlas
segmentation methods consist of two steps, specifically image registration
(rigid or non-rigid) and label merging. ICL requires as input a few markers per
volume to define a RoI and the registration process is carried out by a
landmark-based image registration only in the RoI for the RV, while the CMIC
has a pre-processing step to remove non-relevant structures before the
registration. Also, SBIA performs straight image registration to the entire
atlas w.r.t the target images, which directly affects its performance in terms
of DSC. Nevertheless, these methods have some limitations which include
accuracy performance dependence of the atlas/dataset quality, high
computational cost due to registration between target and multiple atlases. Our
approach overcomes these limitations by considering an RV shape prior as RoI and
using a DH representation under a probabilistic appearance model. Finally, in
[21], is reported a fully automatic joint segmentation of the left and right
cardiac ventricles based on a graph cut framework by using a shape prior. The
shape model is based on multi-atlas non-rigid registration and label merging.
This methodology achieved a DSC average of 0.80 for end-diastole and
end-systole. However, in the case of segmenting the right ventricle during the
entire cardiac cycle, it is necessary to iterate the entire methodology without
taking previous information into account. The proposed approach segmented the
heart cycle over the entire scene without the need for additional information.
This was possible due to prior information being taken into account for the
current frame.
Our approach
introduced a local characterization of the heart region over cine-MRI
sequences. The characterization was achieved by computing a temporal Bayesian
framework with a DHT that allows to localize the region of interest by using
angle and curvature primitives over each pixel. The implemented
characterization results fundamental to understand how the right heart
ventricle shape changes over a cardiac cycle. This dense cardiac Hough
characterization was applied in RV segmentation. In this scenario, the DHT is
fundamental to follow non-parametric regions of interest and to code relevant
information of the heart. Over a public dataset of 95 samples, the proposed
strategy achieved an average score of 0.87 for all slices and 0.92 for basal
slices only.
5.
CONCLUSIONS
In this work was introduced a local
characterization of the right ventricle over cine-MRI sequences. The
characterization was achieved by computing a novel cardiac representation based
on the dense Hough Transform and following a temporal Bayesian framework. This
probabilistic method allows the adaptation of diverse multi-scale temporal
changes during the cardiac cycle. The implemented characterization also allows
to understand how right ventricle shape changes temporarily and achieves an
accurate segmentation. The DHT results fundamental to follow and describe
non-parametric regions of interest such as the RV. Future works will include
the use of additional local primitives to model non-linear behavior of the
heart in terms of its dynamics and shape. Also, an additional evaluation will
be carried out with more rich datasets, for instance, the left ventricle will
be included to evaluate the performance of the proposed approach. Additionally,
a more exhaustive analysis will be carried out on the influence of the update
factor (which was empirically set to a value of 0.1) on the final results.
6.
ACKNOWLEDGEMENTS
The authors
acknowledge the Vicerrectoria de Investigación y Extensión (VIE) of the
Universidad Industrial de Santander for supporting this research work by the
project: “Predicción de patologías cardíacas utilizando representaciones de
aprendizaje profundo en secuencias de resonancia magnética cardíaca (CMR), with
SIVIE code 2703.
7.
REFERENCES
[1] World Health
Organization. (2019). World health statistics 2019: monitoring health for
the SDGs, sustainable development goals. World Health Organization.
[2] Labrador, A. M. A., Martínez, F.,
& Castro, E. R. (2013, November). A novel right ventricle segmentation
approach from local spatio-temporal MRI information. In Iberoamerican
Congress on Pattern Recognition (pp. 206-213). Springer, Berlin,
Heidelberg.
[3] Bernard, O., Lalande, A., Zotti,
C., Cervenansky, F., Yang, X., Heng, P. A., ... & Jodoin, P. M. (2018).
Deep learning techniques for automatic MRI cardiac multi-structures
segmentation and diagnosis: Is the problem solved? IEEE transactions on
medical imaging, 37(11), 2514-2525.
[4] Petitjean, C., Zuluaga, M. A.,
Bai, W., Dacher, J. N., Grosgeorge, D., Caudron, J., ... & Yuan, J. (2015).
Right ventricle segmentation from cardiac MRI: a collation study. Medical
image analysis, 19(1), 187-202.
[5] Vanderpool, R. R., Pinsky, M. R.,
Naeije, R., Deible, C., Kosaraju, V., Bunner, C., ... & Simon, M. A. (2015).
RV-pulmonary arterial coupling predicts outcome in patients referred for
pulmonary hypertension. Heart, 101(1), 37-43.
[6] Buchner, S., Eglseer, M., Debl,
K., Hetzenecker, A., Luchner, A., Husser, O., ... & Arzt, M. (2015). Sleep
disordered breathing and enlargement of the right heart after myocardial
infarction. European Respiratory Journal, 45(3), 680-690.
[7] Gilbert, K., Lam, H. I., Pontré,
B., Cowan, B. R., Occleshaw, C. J., Liu, J. Y., & Young, A. A. (2017). An
interactive tool for rapid biventricular analysis of congenital heart disease. Clinical
physiology and functional imaging, 37(4), 413-420.
[8] Petitjean, C., & Dacher, J.
N. (2011). A review of segmentation methods in short axis cardiac MR images. Medical
image analysis, 15(2), 169-184.
[9] Winter, M. M., Bernink, F. J.,
Groenink, M., Bouma, B. J., van Dijk, A. P., Helbing, W. A., ... & Mulder,
B. J. (2008). Evaluating the systemic right ventricle by CMR: the importance of
consistent and reproducible delineation of the cavity. Journal of
Cardiovascular Magnetic Resonance, 10(1), 1-8.
[10] Tran, P. V. (2016). A fully
convolutional neural network for cardiac segmentation in short-axis MRI. arXiv
preprint arXiv:1604.00494.
[11] El-Rewaidy,
H., Ibrahim, E. S., & Fahmy, A. S. (2016). Segmentation of the right
ventricle in MRI images using a dual active shape model. IET Image
Processing, 10(10), 717-723.
[12] Sedai, S.,
Garnavi, R., Roy, P., & Liang, X. (2015, August). Multi-atlas label fusion
using hybrid of discriminative and generative classifiers for segmentation of
cardiac MR images. In 2015 37th Annual International Conference of the IEEE
Engineering in Medicine and Biology Society (EMBC) (pp. 2977-2980). IEEE.
[13] Xie, L., Sedai,
S., Liang, X., Compas, C. B., Wang, H., Yushkevich, P. A., & Syeda-Mahmood,
T. (2015, April). Multi-atlas label fusion with augmented atlases for fast and
accurate segmentation of cardiac MR images. In 2015 IEEE 12th International
Symposium on Biomedical Imaging (ISBI) (pp. 376-379). IEEE.
[14] Zhen, X., Wang,
Z., Islam, A., Bhaduri, M., Chan, I., & Li, S. (2016). Multi-scale deep
networks and regression forests for direct bi-ventricular volume estimation. Medical
image analysis, 30, 120-129.
[15] Avendi, M. R., Kheradvar, A., &
Jafarkhani, H. (2016). Fully automatic segmentation of heart chambers in
cardiac MRI using deep learning. Journal of Cardiovascular Magnetic Resonance,
18(1), 1-3.
[16] Manzanera, A. (2012). Dense Hough
transforms on gray level images using multi-scale derivatives. In SIXIEME
WORKSHOP AMINA 2012" Applications Médicales de l'Informatique: Nouvelles
Approches".
[17] Duffner, S., & Garcia, C. (2013).
Pixeltrack: a fast adaptive algorithm for tracking non-rigid objects. In Proceedings
of the IEEE international conference on computer vision (pp. 2480-2487).
[18] Luo, G., An, R., Wang, K., Dong, S., &
Zhang, H. (2016, September). A deep learning network for right ventricle
segmentation in short-axis MRI. In 2016 Computing in Cardiology Conference
(CinC) (pp. 485-488). IEEE.
[19] El-Rewaidy, H., Ibrahim, E. S., &
Fahmy, A. S. (2016). Segmentation of the right ventricle in MRI images using a
dual active shape model. IET Image Processing, 10(10), 717-723.
[20] El-Rewaidy, H., & Fahmy, A. S. (2015,
April). Segmentation of the Right Ventricle in MR images using dual active
shape model in the Bookstein coordinates. In 2015 IEEE 12th International
Symposium on Biomedical Imaging (ISBI) (pp. 1320-1323). IEEE.
[21] Maier, O. M., Jiménez, D., Santos, A.,
& Ledesma-Carbayo, M. J. (2012). Segmentation of RV in 4D cardiac MR
volumes using region-merging graph cuts. In 2012 Computing in Cardiology
(pp. 697-700). IEEE.
[22] Zuluaga, M. A., Cardoso, M. J., Modat, M.,
& Ourselin, S. (2013). Multi-atlas propagation whole heart segmentation
from MRI and CTA using a local normalised correlation coefficient criterion. In
International Conference on Functional Imaging and Modeling of the Heart
(pp. 174-181). Springer, Berlin, Heidelberg.
[23] Bai, W., Shi, W., Wang, H., Peters, N. S.,
& Rueckert, D. (2012). Multiatlas based segmentation with local label
fusion for right ventricle MR images. image, 6, 9.
[24] Grosgeorge, D., Petitjean, C., Dacher,
J. N., & Ruan, S. (2013). Graph cut segmentation with a statistical shape
model in cardiac MRI. Computer Vision
and Image Understanding, 117(9),
1027-1035.
![]() to avoid undesired deformations of its morphology,
following a dense per-voxel Hough representation. This template
to avoid undesired deformations of its morphology,
following a dense per-voxel Hough representation. This template ![]() is modeled over each RV heart contour given by a
physician expert. Finally, the non-rectangular RoI (Ω) is estimated according
to a transformed contours average of samples, i.e.,
is modeled over each RV heart contour given by a
physician expert. Finally, the non-rectangular RoI (Ω) is estimated according
to a transformed contours average of samples, i.e., ![]() where
where ![]() corresponds to each sample of a training sequence.
In Figure 1 is illustrated the process of rigid registration of a set of
training samples w.r.t a target. The initial delineation, taken from the
average, is then characterized with the DHT and evolved according to a
statistical framework.
corresponds to each sample of a training sequence.
In Figure 1 is illustrated the process of rigid registration of a set of
training samples w.r.t a target. The initial delineation, taken from the
average, is then characterized with the DHT and evolved according to a
statistical framework.
![]() is computed over a rectangle surrounding RoIs,
centered at position
is computed over a rectangle surrounding RoIs,
centered at position ![]() . Since an MRI sequence is a temporal volume, such a template
can be computed at every slice where cardiac structure exists or can be
computed at independent relevant slices for the analysis (e.g., the basal, mid
and apical slices). The characterized template is then used to search and
detect the respective RoIs in the whole slice for all cine-MRI volumes.
. Since an MRI sequence is a temporal volume, such a template
can be computed at every slice where cardiac structure exists or can be
computed at independent relevant slices for the analysis (e.g., the basal, mid
and apical slices). The characterized template is then used to search and
detect the respective RoIs in the whole slice for all cine-MRI volumes.