Lie Algebra Classification for the Chazy Equation and Further Topics Related with this Algebra

1. INTRODUCTION

The classification of the Lie algebras is a classical problem, which can be reduced to the classification of semi-simple and solvable Lie algebras using the Levi’s theorem. The Levi’s theorem state that for a finite dimensional Lie algebra in a field with characteristic zero it is possible to write this algebra as a direct sum of a solvable Lie algebra and a semi-simple one. For a Good lecture about the classification of Lie algebras the authors recommend see [1, 2, 3, 4]. The theory of the Lie symmetry method is important for different branches of science and engineering because this method helps to study the differential equations that are related to the phenomena that arise in these research areas. In particular, the classification of Lie algebras that are related with this groups of symmetries. Using the Lie algebra it is possible to investigate the automorphism group and use this in turn to study the equations of differences that is associated with the accuracy of numerical analysis methods, see [5, 6, 7].

The classification of the Lie algebra has been carry out in different works. For example in [8] it was presented that the Lie algebra associated to generalizations of the Kummer–Schwarz equation in a particular case is ⊕. Moreover, in [9] the authors classify the Lie algebra corresponding for a Generalization of the Levinson–Smith equation, and it is proved that this Lie algebra is a solvable nonnilpotent five dimensional Lie algebra which is isomorphic to g5,35 in the MubarAkzyanov’s classification. In this sense, this paper is devoted to study the Lie algebra generated by the Lie symmetry group of the equation.

which is known as Chazy equation and was introduced by the same author in [10]. The solution to this equation implies the solution to the equation , which have applications related to the Prandtl boundary layer for a two-dimensional and radial fluid with uniform main current velocity [11]. The optimal algebra and invariant solutions for the Chazy 2 equation (1) is obtained at [12], where the commutators table of the symmetry group of (1) was obtained, which is necessary to the present work too. This paper is devoted to classify the Lie algebra generated by the Lie symmetry group of the Chazy equation and is organized as follows: in section (2) the Lie algebra classification of the Chazy equation is investigated. This Lie Algebra is semisimple, furthermore it will be prove that the Lie algebra of the Chazy equation is isomorphic to the special linear Lie algebra. We also present an applications of this infinitesimal generators by plotting them. Section (3) treats about the calculation of the one parameter subgroup related to the infinitesimal generators of the Chazy equation. The classification of the Lie algebra related to the optimal system is investigated in section (4). Finally, in section (5) some conclusions and future works are given.

2. LIE ALGEBRA CLASSIFICATION FOR CHAZY’S EQUATION

The generating operators of Lie symmetry group to (1) are presented in [13] by the following vector fields:

The above indicates that the vector space generated by the operators described forms a 3-dimensional Lie algebra. Now, in [12], the Table of commutators for the group of symmetries (2) is calculated, see Table 1.

Table 1. Commutators of the symmetry group.

According to the Table (1), we have

Following [14, 2, 15, 16] it is possible to classify the Lie algebra of the group of symmetries (3), by using the next statement over structure constant of any two Lie algebra.

Definition 1

Let g a finite-dimensional Lie algebra over an arbitrary field K. Choose a basis , are called structure constants. The structure constants form a structure tensor, which is an element of the space ⊗ ⊗ g.

Proposition 1

Let and be two Lie algebras of dimensión . Suppose each has a basis with respect to which the structure constant are the same. Then and are isomorphic. We will denote K(., .) to be the Cartan-Killing form. The next propositions can be found in [2].

Proposition 2

(Cartan’s theorem) A Lie algebra is semisimple if and only if its Killing form is nondegenerate. Denote the Lie algebra generated by the vector fields that became of the group Lie point symmetry of the Chazy’s equations.

Let us to consider the brackets relations given in (3). Now we need to calculate the Cartan-Killing form and then check if this Lie algebra is a semisimple Lie algebra by the Cartan’s criterion of semisimple Lie algebras. Since the Killing forms play on important role in the classification of the Lie algebras for example, the Killing form allows us to completely classify real simple algebras, we are going to give explicitly the Cartan-killing for this case. Let that has a basis Π₃, Π₁ and Π₂, regarding this basis we first compute the adjoint representations:

Then, the matrix of the Killing form is

We obtain that the determinant of that matrix is non zero, as a result of that the associated Killing form is a nondegenerate bilinear form and by (2) this Lie algebra is a semisimple Lie algebra.

Denoting the numbers of positive eigenvalues and let denote the numbers of negative eigenvalues, the par is called the signature. Signature is as fundamental to a symmetric bilinear form as eigenvalues are to linear transformations. Finally, using the last definition, so the signature of the Cartan-Killing form associate to the Chazy equation is (2, 1). As a consequence we have the next proposition.

Proposition 3

Let us to consider the basis of the three dimensional Lie algebra of the Lie point group symmetries given by which are defined above. Then the Lie algebra is isomorphic to the special linear Lie algebra, .

Proof. Consider the following assignment , then by substituting in (3) we have and that is we obtain the same structure constant of the , therefore by the proposition 3, and the Lie algebra of the Lie point group symmetries of the chazy equation are isomorphic.

As a consequence of the proposition 3, the Lie algebra of the Chazy equation is a semisimple Lie algebra and consequently its derived Lie algebra is the same Lie algebra, i.e.

Graphics of the infinitesimal generators (2)

The infinitesimal generators (2) have the next graphics

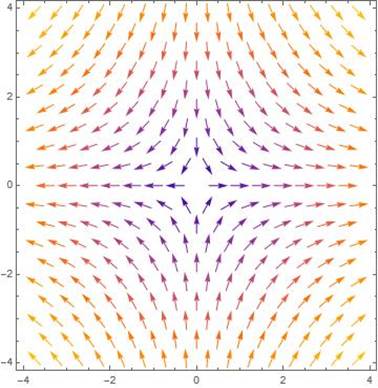
Fig. 1. Infinitesimal generator X₂.

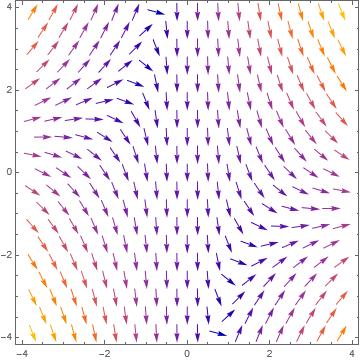
Fig. 2. Infinitesimal generator X₃.

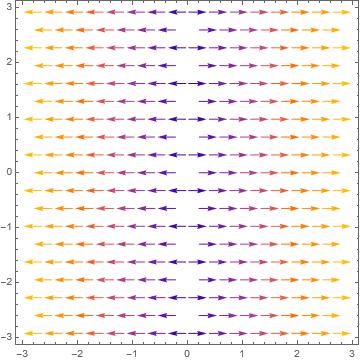
Fig. 3. Infinitesimal generator X₁.

The Fig. 3 represent the infinitesimal generator X₁. This infinitesimal generator is a traslation, that means that the differential equation (1) is invariants under translations. In the same way the Figures 1 and 2, represent the geometry of the one parameter subgroup given in (4) which are associated to the infinitesimal generators X₂ and X₃ respectively.

3. ONE PARAMETER SUBGROUP FOR THE CHAZY EQUATION

As an application of the infinitesimal generators given in (2) of the Lie algebra spanned by this vector fields, we calculate the one parameter subgroup of this Lie algebra. For this purpose it is necessary to solve the following Lie system of differential equations, [17, 18, 19]:

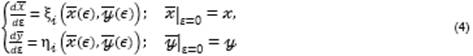
for = 1, 2, 3. where an infinitesimal generator is written in the form

with and differentiable functions. Then for each case of the infinitesimal generators in (2) we solved the system of differential equations (4). Thus, the following proposition holds

Proposition 4

The one-parameter group generated by the symmetries are given by

We also have the inverse transformation

4. CLASSIFICATION RELATED TO THE INFINITESIMAL GENERATORS OF THE OPTIMAL SYSTEM FOR CHAZY EQUATION

In [20], the authors calculated the optimal system for the Chazy Equation (1), obtaining the following generators:

Now we proceed to classify the Lie algebra formed by these elements. The above indicates that the vector space generated by the operators described forms a 4-dimensional Lie algebra. In the Table 2 the commutators of the symmetries is presented.

Table 2. Commutators of the symmetry group for the optimal system.

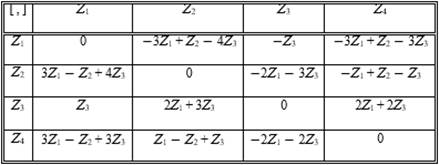
Let us to denote by the Lie algebra spanned by the generators In order to classify the Lie algebra of the optimal system, we first calculate the matrix associated to the Cartan-Killing form:

The determinant of this matrix is zero and by proposition (2) this Lie algebra cannot be a semisimple Lie algebra. Moreover, this Lie algebra is a Levi’s type, that is, a decomposable Lie algebra which is a direct sum of a solvable Lie algebra and a semisimple Lie algebra. Indeed, If we make the next assignment then we obtain the desomposition = ⊕ , where denote the one dimensional abelian Lie algebra. Note that Therefore the next proposition holds

Proposition 5

The Lie algebra associated to the optimal system is isomorphic to g = ⊕ , where denote the one dimensional abelian Lie algebra.

5. CONCLUSION

In this work it was proved that the Lie algebra to the equation (1), is isomorphic to and the signature of the Cartan-Killing form associate to the Chazy Equation is (2, 1). This algebra is a semisimple Lie algebra. The one parameter subgroup is computed, by means that it is the group transformation group. Besides, the Lie algebra classification of the optimal system is performed. This Lie algebra is the Levi’s type. Notice that the Levi subalgebra is in fact the special Linear algebra .

6. ACKNOWLEDGMENTS

Danilo A.G.H is grateful to CAPES, Brazil, for the financial support.

7. DECLARATION INTERESTS

The authors declare that they have no conflict of interest.

8. REFERENCES

[1] R. O. Popovych, V. M. Boyko, M. O. Nesterenko, M. W. Lutfullin, Realizations of real low-dimensional lie algebras, Journal of Physics A: Mathematical and General 36 (26) (2003) 7337. doi: 10.1088/0305-4470/36/26/309

[2] J. E. Humphreys, Introduction to Lie algebras and representation theory, Springer science \& Business media, 2012.9

[3] N. Jacobson, Lie algebras, no. 10, Courier Corporation, 1979.

[4] D. Rand, P. Winternitz, H. Zassenhaus, On the identification of a lie algebra given by its structure constants. i. direct decompositions, Levi decompositions, and nilradicals, Linear algebra and its applications 109 (1988) 197–246. Doi: 10.1016/0024-3795(88)90210-8

[5] A. Bourlioux, C. Cyr-Gagnon, P. Winternitz, Difference schemes with point symmetries and their numerical tests, Journal of Physics A: Mathematical and General 39 (22) (2006) 6877. doi: 10.1088/0305-4470/39/22/006

[6] S. Shen, Lie symmetry reductions and exact solutions of some differential–difference equations, Journal of Physics A: Mathematical and Theoretical 40 (8) (2007) 1775. doi: 10.1088/1751-8113/40/8/006

[7] R. Floreanini, L. Vinet, Lie symmetries of finite-difference equations, Journal of Mathematical Physics 36 (12) (1995) 7024–7042. doi: 10.1063/1.531205

[8] Y. D. Bozhkov, P. R. da Conceição, On the generalizations of the Kummer–schwarz equation, Nonlinear Analysis 192 (2020) 111691. doi: 10.1016/j.na.2019.111691

[9] G. Loaiza, Y. Acevedo, O. Duque, D. A. G. Hernández, Lie algebra classification, conservation laws, and invariant solutions for a generalization of the Levinson–smith equation, International Journal of Differential Equations 2021 (2021) 1–11. doi:10.1155/2021/6628243

[10] J. Chazy, Sur les equations differentielles dont l’integrale generale est uniforme et admet des singelarities essentielles mobiles, C. R. Acad. Sc.Paris 149 (1909) 563–565.

[11] Van Dyke, M. Laminar Boundary Layers, Clarendon Oxford Press, (1964). doi: 10.1017/S0022112064210350

[12] G. Loaiza, O. Duque, Y. Acevedo, Álgebra óptima y soluciones invariantes para la ecuación de Chazy, Ingeniería y Ciencia (2021). doi: 10.17230/ingciencia.17.33.1

[13] R. Naz., F. M. Mahomed, D. P. Mason, Symmetry solutions of a third order ordinary differential equation which arises from Prandtl boundary 10 layer equations, Journal of Nonlinear Mathematical Physics 15 (2008) 179–191. doi: 10.2991/jnmp.2008.15.s1.16

[14] A. Bowers, Classification of three-dimensional real lie algebras, Personal https://cutt.ly/Ad6zozn.

[15] A. W. Knapp, Lie groups beyond an introduction, Springer Science 140. ISBN: 978-1-4757-2453-0.

[16] A. L. Onishchik, E. Vinberg, Lie groups and lie algebras III, Encyclopaedia of Mathematical Sciences 41. Springer, (1994). ISBN 978-3-540-54683-2.

[17] P. J. Olver, Applications of Lie Groups to Differential Equations, Springer-Verlag, (1986). ISBN 978-1-4684-0274-2.

[18] P. Hydon, D. Crighton, Symmetry methods for differential equations: A beginner’s guide, Cambridge Texts in Applied Mathematics, Cambridge University Press, (2000). ISBN-13: 978-0521497862

[19] G. Bluman, S. Anco, Symmetry and integration methods for differential equations, Springer Science and Business Media, (2008). ISBN 978-0-387-21649-2

[20] G. Loaiza, Y. Acevedo-Agudelo, O. Londoño-Duque, Álgebra óptima y soluciones invariantes para la ecuación de Chazy, Ingeniería y Ciencia 17 (33) (2021) 7–21. doi:10.17230/ingciencia.17.33.1