1. INTRODUCTION
A selection of problems in the theory of numbers focuses on mathematical problems within the boundaries of geometry and arithmetic, among these the Mersenne’s primes stand out, due to their computational search and incomprehensible randomness and the finding of even perfect number and it connection to perfect numbers and cryptography [1, 2, 3, 4].
A Mersenne’s prime 
is a prime number of the form 
, where ρ is also a prime number. The current search
for Mersenne’s primes , is led by the GIMPS computational project
(www.mersenne.org) and to date, only 51 of these numbers have been found. In
this work, a study for the Mersenne’s primes under the multiplicative group
modulo 360 is presented with the objective of contributing to this search by
improving the selection processes of the prime exponents and provide a complete
classification of these numbers. The methods used below are proper and basic
under a certain level of number theory [5].
2. CONTEXTUALIZATION
Let be a Mersenne’s prime.
Definition 1 (Ova-angular residue de ). Let be and 
prime numbers. The solution for 
of the equation 
and 
, it will be called Ova-angular of or respectively and will be denoted by 
, 
, such that:
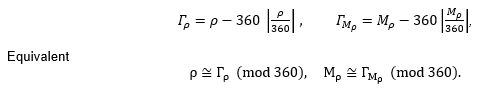
Notice that 
, is the residue that leaves a prime number when it is
divided by some integer, in this case by 360.
Definition 2 ( frequency rotation). Let be 
the set of prime numbers. If 
, then is said that its frequency of rotation denoted 
, is given by the integer part of when divided by 360.
From Definitions 1 y 2, it is true that
Definition 3 (Ova-angular function). Let 
be such that if 
then 
and 
It is clear that
the function 
is well defined, in particular is surjective.
2.1 Complete Classification
Theorem 1 (
Mersenne’s Primes). Let be a prime number and a
Mersenne’s prime. If 
is the set formed by the Ova-angular of the Mersenne primes 
. Then:
Proof. Let be
a Mersenne’s prime, then there exists 
, such that 
. Next we analyze which of the 99 elements are
possible to be Mersenne’s primes, prior to this the following criteria will be
taken into account:
Criterion A. Given the expression 
it
has to 
, which
indicates for 
that
must
be divisible by 2, 4 and 8.
Criterion B. Given the expression 
it
is possible in certain cases that is a multiple of 3 then it has the expression 
. Taking
common factor 3 we have that 
, which is not possible since it contradicts the
fundamental theorem of arithmetic and also 3 does not divide any power of 2.
Consequently, this criterion affirms that cannot
be a multiple of 3.
Criterion C. Given the expression 
it
is possible in certain cases that is a
multiple of 5 then it has the expression 
. Taking common factor 5 we have that 
, which is not possible since 
ends in 5 or 0, and the powers of 2 end in 2, 4, 8,
6, that is; according to the fundamental theorem of arithmetic, 5 does not
divide any power of 2. Consequently, this criterion states that cannot
be a multiple of 5.
Criterion D. Let 
be,
so for these values in the expression 
) it is conditioned that 
must
end in the digit 4. Then 
, this
is 
, then 
is even which would be contradictory since is odd prime. Consequently, this criterion affirms
that 
.
Criterion E. Let 
be, so for this value in equality 
, we have infinite solutions to 
with 
. Which is contradictory to the fact that must be prime. Consequently, this criterion affirms
that 
.
Theorem 2 (Singular Mersenne). The number of Mersenne primes in class 
and in class 
equals 1, i.e. the only Mersenne’s primes with
residues 3 and 7 are 
and in 
respectively.
Proof. For the of the Mersenne primes you get that 
for
some 
integer. Suppose that there is another prime 
with
the same residue and 
. Then this prime must satisfy for integer:
a pure fractional.
Note. is a pure fractional since ends in 
, so it would never be a multiple of 
.
Then is an integer and is a pure fractional 
. Then the only Mersenne’s prime in the class is 
.
Now, for the class of Mersenne primes, we have to: 
. Suppose that there is another prime number 
with the same residue and . Then this prime must satisfy for integer:
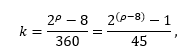
Since is an integer then 
it must end in 
or 
, but since it never ends in ,
then the only option is that it must end in , so 
must end in 
. Then 
, then is an even prime number . Then the only Mersenne’s prime in the class is 
. 
Figure 1 shows all the residuals of the prime numbers
greater than in modulo 
and shows the isosceles trapeze that is formed by
joining Mersenne’s residues with an exponent greater than 
. Hereafter this trapeze will be called Mersenne’s
trapeze.
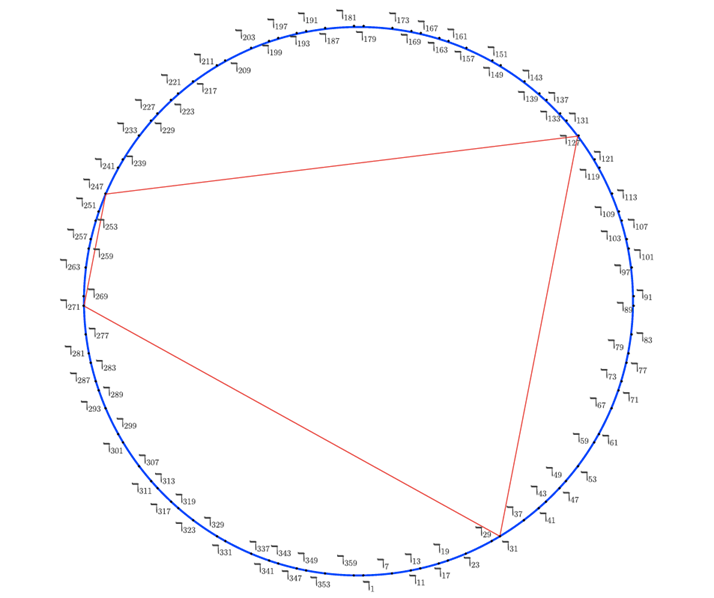
Figure 1. Mersenne’s trapeze.
Theorem 3. Let 
be, then Mersenne’s primes in the class 
are in the sequence:
where
and 
Proof. Since 
then we have that 
, now since is a natural number, then it is convenient analyze
the values of 
for which 
intersects with some natural. Let it be
,
then it is clear that
,
sequence in which
we have the only integer solutions of the required logarithm.
Note.
It’s clear that if 
is prime then it is also a Mersenne’s prime and
according to Dirichlet’s theorem, if there are infinite values of 
that
make prime numbers, then there are infinite Mersenne’s primes.
Corollary 2. For the class 
of Mersenne’s primes, the only for the prime exponent are: 
.
Proof. Analogous to the previous Corollary (1)
proof, only that 
Note.
It’s clear that if 
is prime then it is also a Mersenne’s prime, and
according to Dirichlet’s theorem, if there are infinite values of 
that make prime numbers, then there are infinite
Mersenne’s primes.
Theorem 5. Let 
be, the Mersenne’s primes in the class 
are in the sequence:
where
and 
Proof. Similar to
the proof of the previous Theorem ().
Corollary 3. For the class of Mersenne’s primes, the only
for the prime exponent are: 
.
Proof. Analogous to the previous Corollary (
) proof, only that 
.
Note. It’s clear that if 
is prime then it is also a Mersenne’s prime, and
according to Dirichlet’s theorem, if there are infinite values of 
that make prime numbers, then there are infinite
Mersenne’s primes.
Theorem 6. Let 
be, then Mersenne’s primes in the class 
are in the sequence:
where
and 
Proof. Similar to
the proof of the previous Theorem ().
Corollary 4. For the class of Mersenne’s primes, the only for the prime exponent are: 
.
Proof. Analogous to the previous Corollary () proof, only that 
.
Note.
It’s clear that if 
is prime then it is also a Mersenne’s prime, and
according to Dirichlet’s theorem, if there are infinite values of 
that make prime numbers, then there are infinite
Mersenne’s primes.
All established subgroups for each Mersenne’s prime family are disjoint. This result is consistent with the one
presented in [6].
The reader is invited to articulate the previous
result in a computational way, with the Lucas-Lehmer test or use the Elliptic
curve test method presented in [7], to find a new Mersenne prime 
searching
and testing primes in each of the subgroups presented.
2.2 On residues modulo 360
Theorem 7 (Ova-Ova-Prime-Ova). Let be a prime number, let be 
a completed set of residues of mod ,
let be 
y 
; 
arbitrary
prime numbers. Be also, 
and 
prime numbers such that
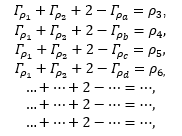
then, at least one of the following is true
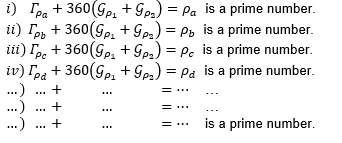
Proof. (by reduction to absurdity). Let
be a prime number, let be a completed set of residues of mod ,
let be y ; arbitrary
prime numbers. Be also, and prime numbers such that
,
it is clear that 
, where 
is a finite set. Suppose that none of the following
is true (Denial of thesis):
So, substituting 
in 
and
after associating and canceling some terms, we have to
The expression 
, would be equivalent to affirming that for every
combination of arbitrary prime numbers, there is no prime that is
the result of 
minus another prime number, which is contradictory
with
the theorem proven by Harald Helfgott in [8], for example, there are the contradictions: 
Thus, it is true that since are arbitrary prime numbers, in one or some cases the
primary arithmetic sum 
will
also be a prime number.
Thus, we arrive at this contradiction for having
denied the thesis, then the assumption initial is false.
Example Theorem 7 (Ova-Ova-Prime-Ova)
Theorem 
establishes that at least one occurs, in this case as
it was chosen at random, seven numbers have turned out, it is fully fulfilled.
Conjecture 1 (The number of primes in the Ova-Ova-Prime-Ova
combination). Although the number of prime numbers resulting from theorem (
) is
at least one, at most, it should be 13.
The reader is invited to verify or solve the previous conjecture in a computational way.
3. CONCLUSIONS
A complete
classification of the Mersenne’s primes was presented through the
multiplicative group modulo 
. A
geometric representation of the residual classes generating these numbers was
obtained. It is possible to continue this work analyzing other applications
that this theory presents using the geometric properties for different prime
numbers, also is possible articulated through computational methods this theory
with different primality tests for these numbers finding a new Mersenne’s
primes (Lucas-Lehmer test or the Elliptic curve test method). The conjecture
about primes in this residual classes was established and the reader is invited
to verify or solve the proposed conjecture in a computational way.
4. ACKNOWLEDGEMENT
The author thanks the EAFIT university for all the support in his research.
5. REFERENCES
[1] I. N. S. Waclaw Sierpinski, M. Stark, (1964). A Selection of Problems in the theory of numbers. Popular lectures in mathematics, Elsevier Ltd, Macmillan Company.
[2] Kenneth H. Rosen, (2011). Elementary number theory and its applications, 6th Edition, Monmouth University.
[3] Y. D. Sergeyev, (2013). Numerical Computations with Infinite and Infinitesimal Numbers: Theory and Applications, 1st Edition, Vol. I, Springer.URL http://wwwinfo.deis.unical.it/~yaro/DIS_book_Sergeyev.pdf
[4] M. T. Hamood, S. Boussakta, (2014). Efficient algorithms for computing the new Mersenne number transform, Digital Signal Processing 25. 280 – 288. doi: https://doi.org/10.1016/j.dsp.2013.10.018.
[5] C. W., (2006). Number theory: an introduction to mathematics, Vol. Part A-B, Springer.
[6] C. E. G. Pineda, S. M. García, (2011). Algunos tópicos en teoría de números: Números Mersenne, teorema Dirichlet, números Fermat, Scientia et Technica 2 (48). 185–190. doi: https://doi.org/10.22517/ 23447214.1279.9
[7] B. H. Gross, (2005). An elliptic curve test for Mersenne primes, Journal of Number Theory 110 (1). 114 – 119, Arnold Ross Memorial Issue. doi: https://doi.org/10.1016/j.jnt.2003.11.011.
[8] H. Helfgot, (2013). Mayor arcs for Goldbach problem, arXiv 14 (1) (2013) 1–79. URLhttps://arxiv.org/abs/1305.2897