ANÁLISIS DE UN CONTROLADOR ADAPTABLE CON OBSERVADOR DE ESTADO POR MODOS DESLIZANTES PARA UN MODELO DE TRATAMIENTO DE DIABETES TIPO 1

 

María F. Villa-Tamayo¹, Juan David Nuñez-López², Juan Pablo Arango-Restrepo³, Héctor A. Botero-Castro⁴

 

¹ Ingeniera de Control.

² Grupo de Investigación en Procesos Dinámicos Kalman.

³ Ingeniero Químico

⁴ Grupo de Investigación en Procesos Dinámicos Kalman.

^{1 2 3 4} Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia.

Correo de correspondencia: jununezl@unal.edu.co

 

RESUMEN

 

El desarrollo del Páncreas Artificial, el cual consiste en la implementación de una bomba de infusión continua de insulina y de sensores para el monitoreo de glucosa en la sangre, es una prioridad para el tratamiento de personas con diabetes tipo 1. Para lograr la automatización completa de este proceso se han propuesto varias estrategias de control con el objetivo de mantener los niveles de glucosa en la sangre en el rango de normoglucemia. Entre las estrategias desarrolladas se destacan las basadas en control adaptable, para contrarrestar el efecto de las variaciones fisiológicas inherentes al paciente. Sin embargo, estas estrategias requieren la medición completa del estado, lo cual no es una tarea fácil debido al costo de los sensores y a la dificultad inherente en la medición directa de variables fisiológicas. Por lo tanto, en este trabajo se usa una estrategia de control adaptable con estabilidad garantizada para un modelo de control de insulina y se diseña un observador de estado no lineal por modos deslizantes, con el fin de estimar las variables de estado que requiere el controlador. Con el sistema completo control-observador se logran resultados satisfactorios al compensar la ingesta de alimentos y los errores entre los parámetros del modelo y del sujeto.

 

Palabras clave: Control Adaptable, Modelo Glucosa- Insulina, Diabetes Mellitus Tipo 1, observador por modos deslizantes.

 

Recibido: 15 de octubre de 2020. Aceptado: 14 de diciembre de 2020

Received: October 15, 2020.     Accepted: December 14, 2020

 

ANALYSIS OF AN ADAPTIVE CONTROLLER WITH A SLIDING MODE STATE OBSERVER FOR A MODEL OF TYPE 1 DIABETES TREATMENT

 

ABSTRACT

 

The development of the Artificial Pancreas, which consists of the implementation of a continuous insulin infusion pump and sensors for blood glucose monitoring, is a priority for the treatment of subjects with type 1 diabetes. To achieve a complete automation of this process several control strategies have been proposed with the aim of maintaining blood glucose levels in the normoglycemic range. Among the developed strategies, those based on adaptive control stand out, to counteract the effect of physiological variations that are inherent to the patient. However, these strategies require full state measurement, which is not an easy task because of sensors cost and the inherent difficulty in direct measurement of physiological variables. Therefore, in this work, an adaptive control strategy with guaranteed stability is used for an insulin control model, and a nonlinear sliding mode observer is designed to estimate the state variables that the controller requires. With the complete control-observer system, satisfactory results are obtained by compensating for meal intake and errors between the model and subject parameters.

 

Keywords: Adaptive Control, Glucose-Insulin Model, Type 1 diabetes mellitus, sliding modes observer.

Cómo citar este artículo: M. Villa, J. Nuñez, J. Arango, H. Botero. “Análisis de un controlador adaptable con observador de estado por modos deslizantes para un modelo de tratamiento de diabetes tipo 1”, Revista Politécnica, vol.16, no.32 pp.19-30, 2020. DOI:10.33571/rpolitec.v16n32a2.

 

1. INTRODUCCIÓN

La diabetes mellitus tipo 1 (T1DM, por sus siglas en inglés) es una enfermedad autoinmune en la cual se destruyen las células beta del páncreas encargadas de la secreción de insulina y por ende se pierde la capacidad de regular la concentración de glucosa en la sangre (BG, por sus siglas en inglés). Los pacientes con T1DM requieren un tratamiento durante toda la vida, el cual consiste en aplicaciones de insulina exógena para restablecer los niveles de BG a un estado de normoglucemia (70mg/dl  BG  180 mg/dl) [1]. Uno de los tratamientos con creciente acogida es el “Páncreas Artificial”, conformado por un sensor continuo de glucosa, una bomba de infusión continua de insulina y un algoritmo de control, para emular el comportamiento natural del páncreas.

 

Para ello, diferentes estrategias de control se han formulado para la regulación de BG, entre las cuales destacan el control proporcional-integral-derivativo (PID), el control predictivo basado en modelo (MPC, por sus siglas en inglés) y el control por lógica difusa [2], [3], [4]. No obstante, las variaciones fisiológicas en un paciente ocasionadas por el ejercicio, el estrés, el fenómeno del alba, entre otras, y las perturbaciones como la ingestión de comidas, continúan siendo uno de los mayores desafíos en el control de la glucemia [5], [6], [2]. Estas variaciones tienen como consecuencia un cambio de los requerimientos de insulina que se debe administrar para evitarle al paciente un estado de hipoglucemia o hiperglucemia [7].

 

En la última década se ha incrementado el interés por estrategias de control adaptable para dar una solución que considere esas variaciones fisiológicas. Estas estrategias se han abordado para cambiar los parámetros del modelo de referencia de la glucosa (control adaptable indirecto) o para sintonizar directamente los parámetros de control (control adaptable directo). En [5] y [6] se presenta una revisión bibliográfica acerca de los diferentes acercamientos a las estrategias de control adaptable aplicables en el tratamiento de T1DM. Entre estos se resalta el control por mínima varianza, el regulador de auto-sintonía, el control lineal gaussiano y el control predictivo generalizado. En estos sistemas se realiza una identificación del modelo en cada periodo de tiempo, con el fin de mejorar el desempeño del sistema de control.

 

Entre las estrategias de control adaptable directo se destacan las que ajustan las matrices de penalización del MPC. Para ello, se han propuesto reglas de sintonía según el desempeño del controlador en cada día [8], y acercamientos a la “Programación de ganancias” en las matrices de penalización del MPC según la zona en que se encuentra la glucemia y su tasa de cambio en cada instante de tiempo [7], [9], [10]. Por otro lado, en [11] se detalla un ajuste del basal de insulina según las zonas definidas por el valor de la glucosa y su tasa de cambio, sin requerir de un modelo de la planta.

 

Dos algoritmos para ajustar el basal postprandial o el bolo pre-comidas se presentan en [12] con base en el comportamiento de la glucosa en una ventana de tiempo después de la última comida. Finalmente, en [13] se establece un conjunto de leyes adaptables con una nueva ley de control que garantizan la estabilidad del sistema por medio de la estrategia de control por modelo de referencia.

 

Esta última estrategia se destaca por utilizar leyes adaptables basadas en la teoría de estabilidad de Lyapunov, con aplicación directa a las dinámicas de un modelo de T1DM. Con este control se logra un ajuste de los parámetros del modelo de referencia y de la ley de control en cada instante de tiempo hasta alcanzar la correcta regulación en la zona de normoglucemia a pesar de las diferencias entre la planta y el modelo [13].

 

Sin embargo, en el planteamiento de la estrategia de control mencionada, y en muchas que se han propuesto en la literatura, se asume la medición completa del estado, compuesto por las concentraciones de glucosa en sangre (glucemia), insulina en plasma e insulina remota. Adicionalmente, se supone que también se puede medir la perturbación por la ingesta de carbohidratos. En la práctica    solo se dispone de un sensor para monitorear la glucemia. Por lo tanto, en este trabajo se propone un esquema compuesto por el controlador descrito en [13] y un observador de estado no lineal por modos deslizantes propuesto en [14], tal que solo se requiere la medición de la concentración de glucemia para lograr el control. Todo el esquema es aplicado en un modelo no lineal de T1DM.  Por lo tanto, el objetivo de este trabajo consiste en diseñar el observador de estado no lineal, de forma que el controlador solo requiera la medición de una variable físicamente medible.  Para lograr este objetivo, se analiza la observabilidad no lineal del modelo, se diseña el observador no lineal por modos deslizantes y se prueba el esquema completo bajo un escenario de variaciones simultáneas en todos los parámetros de la planta e ingesta de comidas.

 

El trabajo está organizado de la siguiente forma: en la Sección 2 se explica el modelo de la relación Glucosa-Insulina-Carbohidratos; en la Sección 3 se retoma la estrategia de control adaptable reportada en [13]; a continuación, en la Sección 4 se analiza la observabilidad del sistema y se diseña un observador por modos deslizantes, el cual es posteriormente incorporado a la estrategia de control. Para verificar los resultados, en la Sección 5 se muestran y analizan las diferentes simulaciones. Finalmente, en la Sección 6 se muestran las conclusiones del trabajo.

 

2. MATERIALES Y METODO

2.1.  Ecuaciones

Con el propósito de describir la interacción de la glucosa en la sangre y la absorción de insulina y carbohidratos se han desarrollado una gran variedad de modelos. Estos se clasifican en modelos mínimos orientados al control y modelos máximos que buscan la representación en detalle de las dinámicas del tratamiento de la diabetes. El modelo más utilizado para la formulación de estrategias de control es el modelo mínimo de Bergman [15], el cual ha sido modificado para incluir la perturbación del sistema a causa de la ingesta de alimentos, tal y como se reporta en [16]. Este último modelo es el seleccionado en este trabajo, y se caracteriza por ser un modelo no lineal con las dinámicas de la glucemia, insulina y carbohidratos descritas de la forma compartimental:

 

,
,	(1)
,
,

 

donde  es la concentración de glucemia (mg/dl),  es la concentración de insulina remota (min^-1),  es la concentración de insulina en plasma (mU/l) y  es la concentración de la perturbación provocada por la ingesta de carbohidratos (mg/dl/min). Los parámetros  y , corresponden a los valores basales de concentración de insulina y de glucemia respectivamente. Las entradas del sistema son  la insulina exógena (mU/l/min) y  los carbohidratos ingeridos (mg/dl/min). La salida del modelo corresponde a la concentración de glucemia .

 

Adicionalmente, los parámetros del sistema tienen el siguiente significado fisiológico:  (min^-1), representa la utilización de glucosa independiente de la insulina,  (l/(min.mU)) es la sensibilidad a la insulina,  (min^-1) es la tasa de degradación de insulina y  (min^-1) es la tasa de aparición de glucosa en plasma a causa de comidas. Se resalta que los parámetros  del modelo (1), varían de paciente a paciente (variaciones inter-paciente) y en un mismo paciente a lo largo del tiempo (variaciones intra-paciente), por eventos como el ejercicio, el estrés, las infecciones, entre otras, y por los cambios fisiológicos en la sensibilidad a la insulina. Por lo tanto, se hacen necesarias estrategias de control que puedan compensar dichas variaciones para regular adecuadamente la glucemia en los pacientes.

 

2.2.  Estrategia de control adaptable

En esta sección, se describe el diseño del controlador adaptable con base en un modelo de referencia y con garantía de estabilidad según lo desarrollado en [13]. El objetivo de control consiste en regular los niveles de BG dentro de la zona de normoglucemia a pesar de las variaciones fisiológicas que puedan presentarse en el paciente. La base de la formulación de la estrategia de control adaptable puede dividirse en tres partes fundamentales: un modelo de referencia, las leyes adaptables para los parámetros y la ley de control.

 

El modelo de referencia a considerar es una copia del modelo de la planta (1), donde las variables de estado y parámetros tienen la misma interpretabilidad. Sin embargo, para este modelo de referencia la señal de entrada se establece como , a la cual se espera que converja el valor basal de infusión de insulina  que se administra a la planta. Así, el modelo de referencia queda dado por:

 

	(2)

 

donde es de recalcar que los parámetros estimados  son los parámetros por ajustar en cada instante de tiempo y  son las variables de estado estimadas del modelo de referencia. Con el propósito de encontrar las leyes de ajuste de los parámetros, se parte de la dinámica del error definido como  obteniéndose: 

 

	(3)

 

con . Luego, se elige una función de Lyapunov candidata de la forma:

 

(4)

 

cuya derivada es:

 

(5)

 

A continuación, para garantizar la estabilidad en el sentido de Lyapunov, se establecen las dinámicas de los parámetros estimados, las constantes  y la ley de control, como aquellas que satisfagan la positividad de la función candidata  y que logren que su derivada  sea semidefinida negativa. Procediendo con esto, las leyes de ajuste de los parámetros se definen como:

 

	(6)
,

 

y la ley de control queda de la forma:

 

(7)

donde las ganancias  y  se fijan en los valores que se muestran en la Tabla 1. Detalles adicionales pueden ser consultados en [13].

 

Tabla 1. Ganancias del controlador

 

2.3.  Diseño del observador de estado por modos deslizantes

 

Es de recalcar, que la ley de control y las leyes adaptables para los parámetros del modelo de referencia en la sección anterior dependen de las cuatro variables de estado y  Sin embargo, en la práctica sólo se puede medir la concentración de glucosa en la sangre, por lo que se hace necesario estimar el valor de las otras variables. En esta sección, se realiza una prueba de observabilidad no lineal al modelo (1) y se diseña un observador de estados por modos deslizantes no lineal para resolver este problema.

 

Subsección 1: Análisis de la observabilidad no lineal del modelo

Teniendo en cuenta que la salida del sistema es la concentración de glucemia, es decir,  se realiza la prueba de observabilidad no lineal por medio del Álgebra de Lie. Las derivadas de Lie para construir el espacio de observación son de la forma [17]:

 

(8)

 

Siendo  y  con  donde  es el número de variables de estado del modelo y es la derivada de Lie de orden . Al realizar el primer paso se procede a encontrar la matriz de observabilidad no lineal (9)

 

 

Los resultados para las derivadas de L_f^n-1 son:

 

 

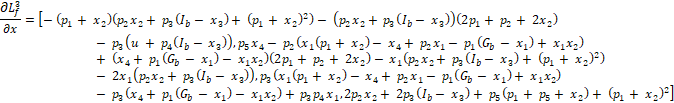
Evaluando el rango de la matriz de observabilidad no lineal (9) se encuentra que la dimensión del espacio imagen es igual a 4, lo cual coincide con la dimensión del espacio de estado. Por lo tanto, todas las variables de estado son observables conociendo la medida de  y de las entradas. Desde el punto de vista físico del modelo, la única forma de perder observabilidad es que el estado  sea cero, lo cual no es posible ya que esta variable representa la concentración de glucemia en un paciente vivo.

 

Subsección 2: Diseño del observador no lineal de estado

A continuación, se procede con el diseño de un observador de estados por modos deslizantes no lineal para estimar las variables de estado  y  las cuales no son medibles por ser variables internas en el cuerpo humano y por lo tanto no se cuenta con sensores. El observador por modos deslizantes retoma el modelo representado de la forma [14]:

 

 

	(10)

 

que en este caso corresponde al modelo (1) con salida  La forma general del observador por modos deslizantes es:

 

	(11)

 

el cual consiste en una copia del modelo (1) evaluado en el estado estimado y un factor de corrección que introduce propiedades de modos deslizantes. Adicionalmente,  es un vector de ganancias de dimensión  el cual contiene las ganancias del observador de la forma y  es la función signo. Para el diseño del observador se usa el error de estimación en la variable medida para generar una superficie deslizante de la forma:

 

(12)

 

Por lo tanto, el observador queda de la forma:

 

	(13)

 

La ganancia  se selecciona para que el error en la variable medida tienda a cero en tiempo finito. Si el valor de esta constante se hace grande, el tiempo de convergencia es pequeño, pero aumenta el chattering en las variables estimadas, por lo tanto, hay un compromiso entre la magnitud del chattering admitido y el tiempo de convergencia requerido. Para las dinámicas de las otras variables estimadas,  a  se usa el concepto de dinámica equivalente según Filippov [18], con el objetivo de diseñar un observador de orden reducido con dinámica de error asintótica. Par ello se obtiene el modelo linealizado de la dinámica reducida como:

 

(14)

 

donde  es un vector que contiene la desviación del error de estimación en las variables  a  y  es el vector de ganancias. Las matrices de la ecuación (14) quedan definidas como:

 

	(15)
	(16)

 

Ahora, la matriz de observabilidad del sistema reducido queda:

 

(17)

 

la cual tiene rango completo si  es diferente de cero, lo cual ocurre siempre ya que  es la concentración de glucemia. Con base en la ecuación (14) se puede diseñar entonces un observador asintótico tal que los polos de la dinámica reducida queden en las ubicaciones deseadas. Así, usando la fórmula de Ackermann se obtiene:

 

(18)

 

y cada una de las ganancias desde  hasta  para el observador de (13) se calculan como:

(19)

El proceso se realiza de manera dinámica, ya que las matrices  y  dependen del estado estimado.

 

3. RESULTADOS

3.1.  Resultados del control adaptable

Con el fin de evaluar la estrategia de control en el tratamiento de la T1DM se propone un escenario de simulación de 720 min (12 horas), en el que se considera una comida de 10 mg/dl/min a las 7 horas. Las condiciones iniciales para la planta y modelo de referencia se establecen como  y . Adicionalmente, se asumen los parámetros del paciente (la planta) como  y ; y se considera un error del 5% en todos los parámetros para el modelo de referencia.

 

En la Figura 1 se observan las dinámicas correspondientes a las concentraciones de glucemia, insulina remota, insulina en sangre y la perturbación ocasionada por la ingesta de comida en el paciente, junto con su correspondiente variable de estado en el modelo de referencia al aplicar la estrategia de control adaptable.  En la Figura 2 se muestra la referencia del esfuerzo de control y el esfuerzo generado por el controlador.

 

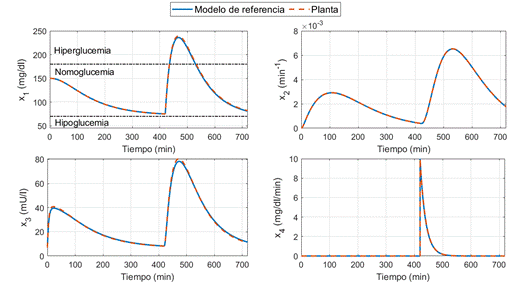
Figura 1. Comparación de la respuesta del sistema y del modelo de referencia con control adaptable.

 

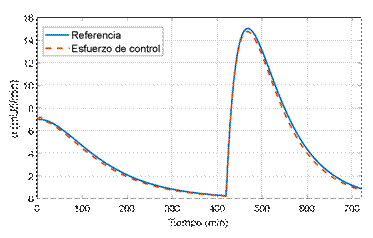
Figura 2. Insulina exógena calculada por el control adaptable.

 

3.2.  Resultados del observador por modos deslizantes

Los resultados de simulación del observador para el proceso descrito se muestran en la Figura 3. El valor de  fue ajustado en 3 para lograr una respuesta rápida y bajo chattering. Los tres polos deseados fueron ubicados en s1 = −0.05, s2 = −0.2 y s3 = −0.1 para la dinámica reducida. La condición inicial para el estado del sistema es  mientras que para el estimador es , es decir se supone un error inicial del 10 % en los estados y . Adicionalmente, se supone un error constante planta-modelo del 5 % en todos los parámetros del observador.

 

 

Figura 3. Dinámica de los errores de estimación en las variables de estado.

 

3.3.  Resultados del acople del controlador adaptable y el observador por modos deslizantes

Con el fin de verificar el comportamiento del esquema completo controlador-observador (como se muestra en la Figura 4), se realiza una simulación en lazo cerrado bajo un escenario de 1440 minutos (24 horas) con tres comidas: un desayuno de 6 mg/dl/min a las 7h, un almuerzo de 10 mg/dl/min a las 12h y una cena de 8 mg/dl/min a las 19h. Las condiciones iniciales del estado del sistema se establecen como  y las del estimador como , es decir, se supone un error inicial del 10 % en la concentración de glucemia y en concentración de insulina en plasma. Adicionalmente, se considera un error inicial en los parámetros del modelo de referencia del 5 % con respecto a los parámetros de la planta. Los resultados se pueden observar en las Figuras 5 a 7.

 

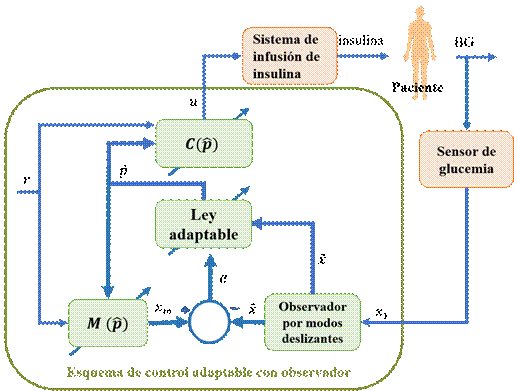
Figura 4. Esquema de control adaptable con observador. se refiere al modelo de referencia y  a la ley de control. Puede verse que ambas dependen de la adaptación de los parámetros . La ley de control calcula la cantidad de insulina que debe aplicarse al paciente y al esquema de control-observador llega la información sobre la concentración de glucosa en sangre (BG) medidos por el sensor.

 

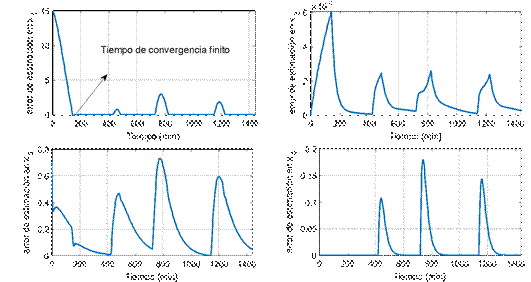
Figura 5. Dinámica de los errores de estimación en las variables de estado.

 

 

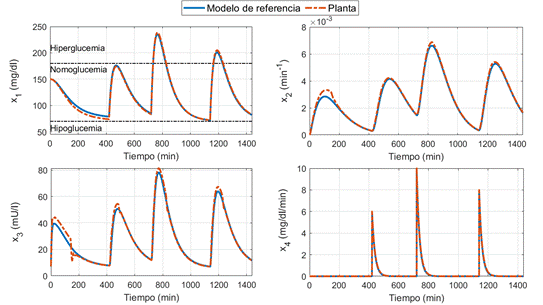
Figura 6. Respuesta del sistema y del modelo de referencia de la glucosa en sangre.

 

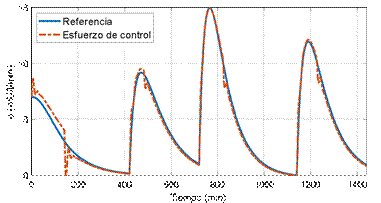
Figura 7. Esfuerzo de control.

 

 

4. ANÁLISIS DE RESULTADOS

En la Figura 1 puede verse como el estado se ajusta a la evolución del modelo de referencia compensando adecuadamente la perturbación por comida, además de tener en cuenta la diferencia planta-modelo representada en las condiciones iniciales de los parámetros del modelo de referencia. En la concentración de glucemia del paciente (estado ) se evidencia como esta se regula dentro de la zona de normoglucemia. Tras la perturbación por carbohidratos los niveles de BG aumentan hasta hiperglucemia, pero regresan a la zona deseada en un tiempo menor a 2 horas. Adicionalmente, en la Figura 2 se muestra la insulina administrada, la cual sigue la referencia planteada .

 

Los resultados de simulación del observador para el proceso descrito se muestran en la Figura 3. Se puede observar en la Figura 3 (superior-izquierda) la convergencia en tiempo finito del error en , mientras que la convergencia de los demás errores se produce de forma más lenta. Es claro que todos los errores de estimación convergen a cero. Al momento de la ingesta de carbohidratos, el error en las variables de estado aumenta, dado el error planta modelo por el cambio en las entradas  y . No obstante, este logra compensarse adecuadamente, y el observador elimina el error con respecto a la planta.

 

Para el conjunto controlador-observador los resultados se pueden observar en las Figuras 5 a 7. En este caso, fue necesario aumentar el tiempo de establecimiento del observador respecto al diseñado en la sección anterior, debido a que con una velocidad de convergencia mayor a la propuesta aquí se producen sobre picos excesivos en las variables de estado en lazo cerrado, además de chattering en el esfuerzo de control. Por lo tanto, la ganancia se estableció en 0.05, y los polos deseados para la dinámica reducida se ubicaron en s₁ = −0.04, s₂ = −0.2, s₃ = −0.05. En la Figura 5 se puede ver la convergencia en tiempo finito del error de estimación en  y la convergencia asintótica de los demás errores de estimación.

 

Finalmente, el seguimiento de variables cuando se tiene el sistema en lazo cerrado con el observador se puede notar en la Figura 6. Es posible identificar una pérdida de seguimiento de variables de estado debido a la dinámica introducida por el observador de estado. Sin embargo, a medida que el tiempo crece, el error con respecto al modelo de referencia tiende a disminuir. Finalmente, el esfuerzo de control se puede observar en la Figura 7, cuya evolución muestra mayores variaciones dada la influencia del observador de estado y su efecto directo en la ley de control.

 

5. CONCLUSIONES

En este artículo se aplicó una estrategia de control adaptable y se diseñó un observador de estado por modos deslizantes no lineal para un modelo de control de insulina. La estructura control-observador propuesta busca reducir el número de variables de estado que se deben medir, a la vez que trata de mantener una variación dinámica de las variables de estado dentro de los límites permisibles. Con este estudio se pudo concluir que el observador de estado no lineal puede estimar todas las variables de estado a partir de la medición de la concentración de glucemia. Así mismo, se logró analizar que el observador introduce una dinámica adicional al sistema de control, produciendo un mayor error respecto al caso ideal, en el cual se miden todas las variables de estado. Sin embargo, los resultados de simulación son satisfactorios y se espera en el futuro probar la estabilidad del conjunto y mejorar su desempeño. La aplicación práctica de este tipo de estrategias de control y estimación de estado permitirá construir en el futuro bombas de insulina de bajo costo.

 

6. REFERENCIAS BIBLIOGRÁFICAS

 

[1] Poretsky, L. (2010). Principles of Diabetes Mellitus. New York: Springer.

 

[2] Fathi, A. E., Smaoui, M. R., Gingras, V., Boulet, B. y Haidar, A. (2018). The artificial pancreas and meal control: An overview of postprandial glucose regulation in type 1 diabetes. IEEE Control Systems, 38(1), 67-85.

 

[3] Hovorka, R. (2006). Continuous glucose monitoring and closed-loop systems. Journal of Diabetes Science and Technology, 23(1), 1-12.

 

[4] Pinsker, J. E., Lee, E., Dassau, J. B., Seborg, D. E. Bradley, P. K., Gondhalekar, R., Bevier, W. C., Huyett, L., Zisser, H. C. y Doyle, F. J. (2016). Randomized crossover comparison of personalized mpc and pid control algorithms for the artificial pancreas. Diabetes Care, 39, 1135–1142.

 

[5] Turksoy, K. y Cinar, A. (2014) Adaptive control of artificial pancreas systems - a review. Journal of Healthcare Engineering, 5(1), 1-22.

 

[6] Haidar, A. (2016). The artificial pancreas: How closed-loop control is revolutionizing diabetes. IEEE Control Systems, 36(5), 28-47.

 

[7] Grosman, B., Dassau, E., Zisser, H., Jovanovic, L. y Doyle III, F. J. (2011). Multi-zone-mpc: Clinical inspired control algorithm for the artificial pancreas. IFAC Proceedings Volumes (IFAC-PapersOnline), 44, 7120–7125.

 

[8] Turksoy, K., Bayrak, E. S., Quinn, L., Littlejohn, E. y Cinar, A. (2013). Multivariable adaptive closed-loop control of an artificial pancreas without meal and activity announcement. Diabetes Technology and Therapeutics, 15(5), 386–400.

 

[9] Abu-Rmileh, A. y Garcia-Gabin, W. (2010). A gain-scheduling model predictive controller for blood glucose control in type 1 diabetes. IEEE Transactions on Biomedical Engineering, 57(10), 2478–2484.

 

[10] Shi, D., Dassau, E. y Doyle III, F. J. (2019). Adaptive zone model predictive control of artificial pancreas based on glucose- and velocity-dependent control penalties. IEEE Transactions on Biomedical Engineering, 66(4), 1045–1054.

 

[11] Wang, Y., Dassau, E., Zisser, H., Jovanovic, L. y Doyle III, F. J. (2010). Automatic bolus and adaptive basal algorithm for the artificial pancreatic β-cell. Diabetes Technology and Therapeutics, 12(11), 879–887.

 

[12] Resalat, N., El Youssef, J., Reddy, R., Castle, J. y Jacobs, P. G. (2019). Adaptive tuning of basal and bolus insulin to reduce postprandial hypoglycemia in a hybrid artificial pancreas. Journal of Process Control, 88, 247–254.

 

[13] Nath, A., Deb, D., Dey, R. y Das, S. (2018). Blood glucose regulation in type 1 diabetic patients: an adaptive parametric compensation control-based approach. IET Systems Biology, 12(5), 219–225.

 

[14] Wang, G. B., Peng, S. S y Huang, H. P. (1997) A sliding observer for nonlinear process control. Chemical Engineering Science, 52(5), 787 – 805.

 

[15] Bergman, R. N., Phillips, L. S. y Cobelli, C. (1981). Physiologic evaluation of factors controlling glucose tolerance in man. measurement of insulin sensitivity and β-cell glucose sensitivity from the response to intravenous glucose. Journal of Clinical Investigation, 68(6), 1456–1467.

 

[16] Batmani, Y. (2017). Blood glucose concentration control for type 1 diabetic patients: a non-linear suboptimal approach. IET Systems Biology, 11(4), 119–125.

 

[17] Khalil, H. K. (1996). Nonlinear Systems. Englewood Cliffs, NJ: PrenticeHall, 2nd ed.

 

[18] Arscott, F. y Filippov, A. (1988). Differential Equations with Discontinuous Righthand Sides: Control Systems. Mathematics and its Applications, Springer Netherlands.