1. INTRODUCCIÓN
En los últimos años con la tendencia por ayudar al medio ambiente y producir energía eléctrica partiendo de energías limpias ha tenido un gran crecimiento, un ejemplo de estas son las energías renovables como la eólica, geotérmica, biomasa, hidroeléctrica se suma la energía producida por corrientes de marea, presentando un potencial energético estimado de alrededor de 600TWh/yr[1]. Colombia cuenta con acceso al mar caribe y pacífico, en donde áreas como el archipiélago de San Andrés y Providencia, el golfo de Urabá y departamentos como el Chocó son zonas no interconectadas (ZNI) y la producción de energía eléctrica de se hace con pequeñas plantas de generación a base de hidrocarburos [2]. Por este motivo, han surgido alternativas de generación amigables con el ambiente y de bajo costo, una de estas soluciones son las turbinas hidrocinéticas de eje vertical. Este tipo de turbinas presentan características interesantes como su capacidad de captar omnidireccionalmente el fluido, es decir, no importa en qué dirección venga el fluido para iniciar con su rotación lo que es importante si se desea implementarlas en el mar, además, no requieren de un mantenimiento riguroso y debido a su geometría tiene una fácil construcción reduciendo su costo de producción[3], sin embargo turbinas como la H-Darrieus presentan eficiencias bajas para ser implementadas a gran escala, por tal motivo, desde hace varias décadas diferentes autores y o investigadores han estudiado y modelado cuales son los parámetros influyentes en la eficiencia y con los cuales se puede generar un mejor diseño.
En el año 1983, J. Baker[4] revisó la incapacidad de auto-arranque en las turbinas eólicas de eje vertical de baja solidez proponiendo varias formas para solucionar este problema, en donde concluyo que haciendo modificaciones en la turbina es posible construir una turbina de eje vertical con la capacidad de autoarranque. Miyake et al. [5] analizó la influencia de diferentes parámetros como la dimensión del rotor, forma del álabe, solidez, etc. Dando como resultado un gráfico para seleccionar la solidez adecuada de acuerdo a la eficiencia hidráulica.
M. J. Khan at al.[6] presentó el análisis para el diseño de una turbina, teniendo en cuenta parámetros como número de álabes, solidez, selección del perfil a usar, etc. Obteniendo como resultados un procedimiento sistemático con información de apoyo para ayudar en la toma de decisiones y realizar el mejor diseño.
Por su parte R. Dominy et al. [7] investigaron computacionalmente los parámetros que influyen en la capacidad de auto-arranque, tales como el número de álabes y la posición inicial de la turbina. Concluyendo que con dos álabes la posición de inicio afectaba directamente la capacidad de iniciar por sí misma, y en la configuración con tres álabes independientemente de su posición inicial, siempre podía iniciar automáticamente.
Mitsuhiro Shiono et al.[8], analizó la influencia que tienen parámetros como la solidez y el número de álabes en una turbina tipo H-Darrieus. En primer lugar, estudió para varias geometrías con diferentes valores de solidez la incidencia que tenía en la generación de torque, seguidamente observo el comportamiento cuando se cambian el número de álabes creando geometrías con dos hasta seis álabes. En cuanto a resultados se observó que la solidez tenía una relación directamente proporcional con la eficiencia de la turbina, por parte del número álabes se notó que cuando estos se aumentan, se reduce la producción de torque negativo, lo que facilita la posibilidad de auto arranque.
Y. M. Dai et al.[9] presentó el análisis de diferentes geometrías de la turbina H-Darrieus, variando parámetros como número de álabes y longitud de cuerda para observar el coeficiente de potencia de acuerdo a la solidez y diferentes velocidades del fluido. Eligio la geometría con mejores características y llevo a cabo simulaciones, obteniendo como resultados la variación de torque producido alrededor de una vuelta completa de la turbina.
C.A. Consul et al. [10] analizaron la influencia que tiene la solidez en la generación de potencia. Tomando en cuenta valores de solidez de 0.019 con dos álabes y 0.038 para cuatro álabes, se encontró que cuando se aumenta el número de álabes el coeficiente de potencia aumento, y que a bajas TSR, la disminución en el ángulo de ataque, debido a una mayor solidez, resulta en un aumento en la sustentación y, por lo tanto, la potencia generada.
I. Hwang et al.[11] determinó las características optimas de operación para una turbina de eje vertical mediante CFD, en donde analizo variables como el número de álabes de, la longitud de cuerda, la velocidad del fluido, etc. Concluyendo que la potencia del rotor alcanza su máximo de potencia a un TSR más bajo, a medida que la solidez del rotor se hace más grande, y el rendimiento del rotor es casi similar cuando se determina que TSR y la solidez del rotor tienen el mismo valor.
Gosselin et al.[12] en el año 2013 estudió los parámetros tales como efecto de la solidez, número de álabes, el número de Reynolds, ángulo de ataque y el grosor de los álabes mediante simulación en turbinas tipo Darrieus en 2D y 3D concluyendo que las turbinas con una solidez mayor a 0.5 no presentan gran eficiencia, sin embargo, al tener esta misma solidez y cambiando el ángulo de ataque mayor a 0 se manifiesta un incremento de sustentación, eficiencia y bajo bloqueo dinámico.
M.H. Mohamed [13] estudió por medio de CFD y experimentalmente la influencia que tiene solidez en la turbina H-Darrieus y el uso de un sistema híbrido para mejorar la capacidad de auto-arranque, dando como resultado, una afectación directa por parte de la solidez, donde se evidencia que este parámetro mejora la capacidad de auto arranque.
O. López et al.[14] estudió el comportamiento de la turbina Darrieus de eje vertical, con énfasis en el análisis de las características hidrodinámicas. Para esto definió una turbina con un diámetro de rotor de 900mm y tres alabes con un tamaño de cuerda de 132mm, además, definieron tres dominios: dos dominios estáticos y uno rotativo tipo anillo en donde se encuentran los álabes siendo el de mayor interés. para luego ser llevado al programa Ansys Fluent® estudiando diferentes modelos de turbulencia. Como resultado se obtuvo el comportamiento y producción de torque de la turbina alrededor de una vuelta.
En este trabajo, presenta el análisis de la influencia del número de álabes en una turbina de eje vertical tipo H-Darrieus para definir cuál es el número de [14]alabes con los cuales se presentan las mayores eficiencias. En la primera parte se definieron las diferentes geometrías, en donde establecieron tres valores de solidez con la intención de reducir el número de variables involucradas en el estudio. En la segunda parte se hace uso del programa Ansys® para hacer la simulación de los respectivos modelos de turbina y obtener los resultados numéricos para seguidamente seguir con su análisis.
2. MODELADO MATEMÁTICO
O. López [14], plantea que la turbina se puede caracterizar por el torque del rotor M, arrastre del rotor D, velocidad angular del rotor ω, y potencia de salida P= ωM. Los parámetros adimensionales principales se presentan en la tabla 1.
![Tabla 1. Principales parámetros.
Parámetros principales
Tip Speed Ratio (TSR) λ= ωR/V_o (1)
Coeficiente de torque
C_(m )= 2M/(ρV_o^2 RS_ref ) (2)
Coeficiente de potencia o eficiencia
C_(p )= 2P/(ρV_o^3 S_ref ) (3)
Coeficiente de arrastre
C_(D )= 2D/(ρV_o^2 S_ref ) (4)
Solidez
σ= Nc/R (5)
Fuente: adaptado de [14].](https://revistas.elpoli.edu.co/index.php/pol/article/download/1659/version/1470/1602/8565/image001.png)
Donde, R representa el radio
del rotor, Vo es la velocidad del fluido, ρ la densidad del fluido y Sref la
sección Transversal (![]() ). Para la solidez se tiene
que N representa el número de alabes y C la longitud de cuerda.
). Para la solidez se tiene
que N representa el número de alabes y C la longitud de cuerda.
3. METODOS
Se inicia haciendo un análisis de solidez mediante la literatura donde se recomienda una solidez mayor a 0.4[8], con el fin de mantener la capacidad de auto-arranque. En el caso presente se ejecutó de 0.89, sin embargo, para el análisis se aplicarán dos valores de solidez adicionales de 0.45 y 1.35 los cuales son indispensables validar la veracidad del mejor punto de solidez.
Para mantener estos valores de solidez constante es necesario fijar un diámetro del rotor y variar el número de álabes al mismo tiempo que la longitud de cuerda. Para esto se toma como referencia un diámetro de 900 mm y se itera el número de alabes desde 2 hasta 10 alabes para cada uno de los valores de solidez. Las diferentes geometrías planteadas se muestran en la tabla 2.
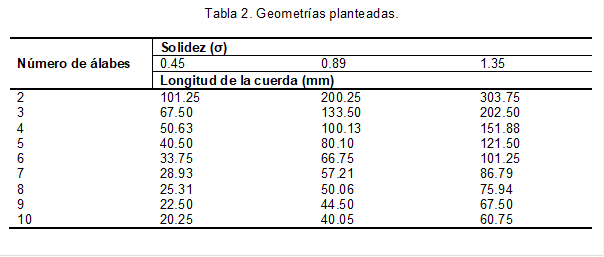
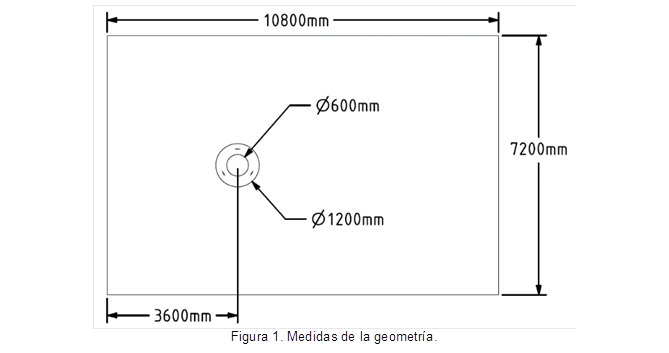
Estas métricas son llevadas al módulo SpaceClaim de Ansys ® donde se exporta la nube de puntos del perfil NACA4415, y se crea la geometría 2D para cada una de las configuraciones. La geometría propuesta se muestra en la figura 1, en donde se tiene una superficie tipo anillo que simula el rotor y dos superficies que representan el interior del rotor y el exterior que simula el canal por donde pasa el fluido.
En el módulo ICEM de Ansys® se realizó la discretización de los 27 rotores dibujados previamente donde se consideran como métricas optimas una relación de aspecto máximo de 27, un ángulo de 18 y una calidad mínima de 0.6; por otra parte, para la geometría 2D se realizó con una Malla tipo cuadrilátero para una mejor respuesta, velocidad de simulación y menor costo computacional.
Las figuras 2,3 y 4 muestran la discretización realizada, donde se evidencia un mayor refinamiento en el rotor y los álabes, con la intención de describir mejor los fenómenos fluido dinámicos que ocurren en las regiones cercanas a los alabes.

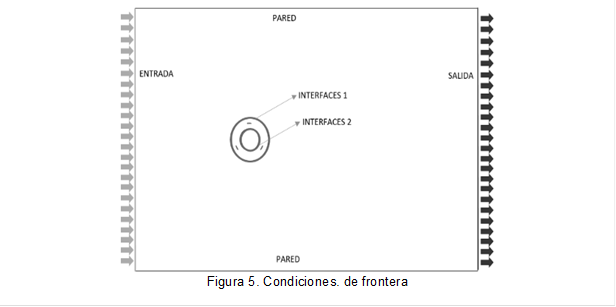
En ANSYS FLUENT ® V19.2 se establecen las condiciones de frontera mostradas en la figura 5, en las que se destacan tres dominios, dos dominios estáticos denominados exterior e interior y un dominio tipo anillo que simula el giro del rotor a una velocidad angular de 6,28 rad/s[14] y es donde se encuentran ubicados los álabes. La interacción entre estos tres dominios está dada por dos interfaces, la primera es entre el dominio exterior y el anillo, y la segunda entre en anillo y el dominio interior.


Así mismo se configura una velocidad de entrada del fluido de 1.62 m/s[14] y una salida de presión a la atmosfera. Se selecciona un modelo de turbulencia SST Transicional para una simulación de 5 vueltas completas del rotor en estado transitorio con un tiempo de paso de 0.005s para 1000 iteraciones.
4. RESULTADOS
La discusión debe considerar los resultados en relación con las hipótesis formuladas en la introducción y el lugar del estudio en el contexto de otros trabajos. Las secciones de Resultados y Discusión (o análisis de resultados) también pueden ser combinadas.
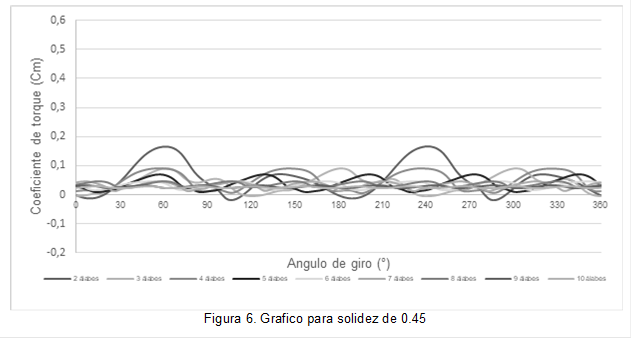
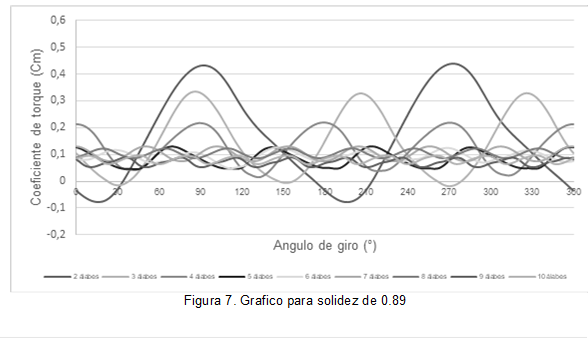
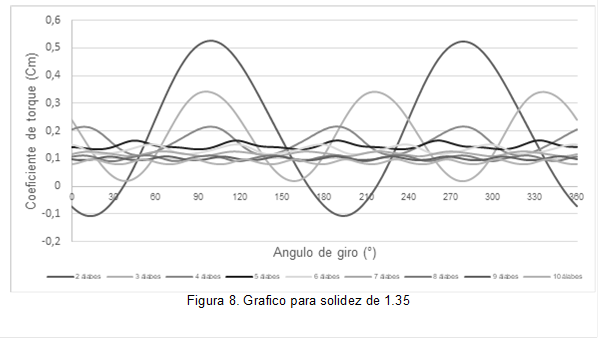
El coeficiente de torque total se muestra en la a figura 6,7 y 8 para las geometrías planteadas con la solidez de 0.45,0.89 y 1.35 respectivamente, en donde se observa un decrecimiento del máximo torque producido a medida que se aumenta el número de álabes lo que conlleva a que la eficiencia disminuya, sin embargo, los coeficientes de torque negativos son eliminados con el aumento del número de álabes, ayudando a que la turbina tenga una mejor capacidad de auto-arranque, en donde se puede notar que con la solidez de 1.35 los torques negativos se eliminan a partir de 3 alabes.
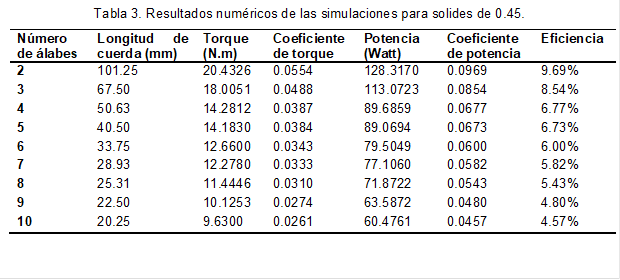
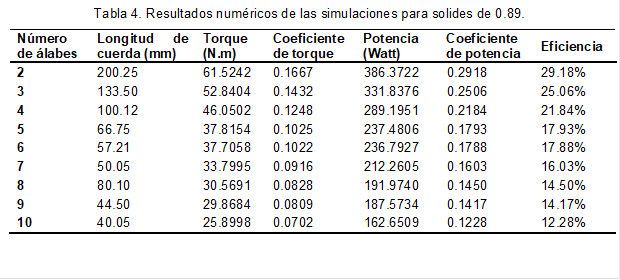
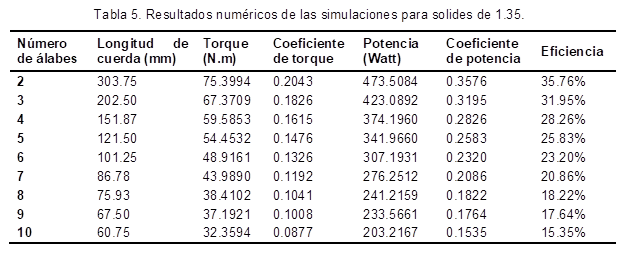
La tabla 3,4 y 5, muestran los resultados numéricos obtenidos de las simulaciones para los valores de solidez planteados. En estas tablas se evidencia mejor el comportamiento de la turbina, el cual conforme se aumenta el número de álabes la eficiencia tiene un decrecimiento notable, por otra parte, se observa que la solidez también tuvo influencia en la eficiencia, es decir, cuando se aumentó la solidez a 1.35 las eficiencias para cada una de las configuraciones de alabes aumento respecto a la de 0.89.
5. CONCLUSIONES
El número de álabes influye directamente con la eficiencia de la turbina, mostrando que cuando este aumenta la eficiencia disminuye. Sin embargo, la disminución del torque negativo mejora a medida que la turbina aumenta el número de álabes, lo que se traduce a una mejor capacidad de auto-arranque. Por otra parte, el valor de la solidez también influyo en la mejora de la turbina, aumentado su eficiencia en donde la configuración de dos álabes y una longitud de cuerda de 303.75 mm se presenta como la más eficiente, pero aun presenta producción de torque negativo, concluyendo así que es necesario mantener el equilibrio entre el número de álabes y el valor de solidez para obtener el diseño más eficiente.
6. AGRADECIMIENTOS
Los autores agradecen a el programa Jóvenes investigadores ITM por el apoyo durante el proceso de investigación.
7. REFERENCIAS BIBLIOGRÁFICAS
[1] D. Kerr, «Marine energy», Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., vol. 365, n.o 1853, pp. 971-992, 2007.
[2] N. A. García, R. H. T. Holguín, y D. A. O. Urrea, ZONAS NO INTERCONECTADAS - ZNI Diagnóstico de la prestación del servicio de energía eléctrica 2017 Superintendencia Delegada para Energía y Gas Combustible, n.o 1. 2017.
[3] S. Del Río Sánchez, «Diseño de un aerogenerador tipo H-Darrieus y estudio de la influencia del ángulo de pitch , mediante Mecánica de Fluidos Computacional», p. 109, 2017.
[4] J. R. Baker, FEATURES TO AID OR ENABLE SELF STARTING OF FIXED PITCH LOW SOLIDITY 6 r q Ct ( oO άφ ( l ), vol. 15. Elsevier BV, 1983.
[5] Y. MIYAKE, K. KOIKE, T. TSUGAWA, y S. MURATA, «Perfomance Characteristics of High Speed-Type Cross Flow Turbine», Bull. JSMe, vol. 27, p. 8, 1984.
[6] M. J. Khan, M. T. Iqbal, y J. E. Quaicoe, «Design Considerations of a Straight Bladed Darrieus Rotor for River Current Turbines A )», vol. 5, n.o 2, 2006.
[7] R. Ã. Dominy, P. Lunt, A. Bickerdyke, y J. Dominy, «Self-starting capability of a Darrieus turbine», vol. 221, pp. 111-120, 2007.
[8] M. Shiono, K. Suzuki, y S. Kiho, «Experimental study of the characteristics of a Darrieus turbine for tidal power generation», Electr. Eng. Japan (English Transl. Denki Gakkai Ronbunshi), vol. 132, n.o 3, pp. 38-47, 2000.
[9] Y. M. Dai y W. Lam, «Numerical study of straight-bladed Darrieus-type tidal turbine», Proc. Inst. Civ. Eng. - Energy, vol. 162, n.o 2, pp. 67-76, 2009.
[10] C. A. Consul, R. H. J. Willden, E. Ferrer, y M. D. Mcculloch, «Influence of Solidity on the Performance of a Cross-Flow Turbine», pp. 484-493, 2009.
[11] I. S. Hwang, Y. H. Lee, y S. J. Kim, «Optimization of cycloidal water turbine and the performance improvement by individual blade control», Appl. Energy, vol. 86, n.o 9, pp. 1532-1540, 2009.
[12] R. Gosselin, G. Dumas, y M. Boudreau, «Parametric study of H-Darrieus vertical-axis turbines using uRANS simulations», 2013.
[13] M. H. Mohamed, «Impacts of solidity and hybrid system in small wind turbines performance», Energy, vol. 57, pp. 495-504, 2013.
[14] O. López, D. Meneses, B. Quintero, y S. Laín, «Computational study of transient flow around Darrieus type cross flow water turbines», J. Renew. Sustain. Energy, vol. 8, n.o 1, 2016.