1. INTRODUCCIÓN
El control de vuelo en los vehículos aéreos no tripulados ha sido un área de investigación a la que se ha prestado gran interés por muchos años. Estas aeronaves son capaces de volar sin necesidad de un piloto humano a bordo que las controle. Pueden ser controladas remotamente o volar de forma autónoma basada en vuelos programados previamente utilizando sistemas de control complejos. En la actualidad, en numerosas universidades y centros de investigación, se analizan, modelan y desarrollan vehículos aéreos autónomos, por ejemplo, las firmas como Lockheed Martin, la NASA y la Universidad MIT, entre otras a nivel mundial y a nivel nacional, en la misma línea de investigación, la Universidad San Buenaventura con el VANT Navigator, la Fundación Universitaria Los Libertadores con el VANT solvendus, el Grupo de Fitotecnia de la U.N. Sede Medellín trabaja en drones para agricultura de precisión, la Universidad EAFIT desarrolla un proyecto enfocado en tres líneas: desarrollo, creación y adaptación de nuevas aplicaciones de los drones.
Las estrategias de control utilizadas son muy diferentes y van desde el uso de controladores PID, hasta sistemas de control inteligentes. En [1] se presenta el proceso matemático para obtener un modelo dinámico de aviones subsónicos, en ecuaciones de espacio de estado para los movimientos longitudinal y lateral. El logro principal de este trabajo radica en la implementación de una metodología para calcular los coeficientes aerodinámicos utilizando una interfaz gráfica. En [2], se modelan, simulan y controlan cinco sistemas aéreos no tripulados, la modelación se basa en la metodología de Newton-Euler y Euler-Lagrange y para el control se utilizan controladores PID y algoritmos basados en lógica difusa y redes neuronales. Así mismo, en [3], se presenta un nuevo sistema de control de vuelo automático basado en la metodología de control predictivo experto, para una aeronave de ala fija de 6 grados de libertad no-lineal, las leyes de control resultantes se validaron mediante simulación con el modelo propuesto. En [4] se desarrolla una herramienta para la identificación de los parámetros de un modelo de una UAV (Unmanned Aerial Vehicle) a partir de sus datos de vuelo, utilizando un estimador de mínimos cuadrados para el procesamiento de datos reales. La importancia del trabajo, realizado en el Instituto Balseiro Universidad Nacional de Cuyo, Argentina, se refleja en la generación de un conocimiento más profundo y práctico acerca de la estimación de parámetros de vehículos aéreos. En [5], se da un acercamiento al modelado y control de aeronaves de ala fija de pequeña envergadura no tripuladas y se presenta un control no lineal a partir del desacople del vuelo lateral y longitudinal mostrando resultados en simulación. En [6] se propone el desarrollo de un sistema de control utilizando técnicas adaptativas que esté en capacidad de absorber las perturbaciones que experimenta una UAV ante la pérdida súbita de una carga que transporta. El trabajo es interesante en cuanto desarrolla un simulador en el cual los datos de entrada, como pueden ser los valores de referencia de la velocidad y del ángulo de trayectoria se pueden modificar fácilmente, lo cual hace posible analizar el desempeño de la aeronave ante diferentes condiciones de operación.
Este artículo tiene como objetivo simular el modelo de la aeronave objeto de estudio e implementar un sistema de control predictivo adaptativo en el entorno de Matlab® y Simulink® capaz de controlar sus movimientos longitudinal y latero-direccional y estabilizarla ante cambios en el punto de consigna y en presencia de perturbaciones. Metodológicamente el trabajo se inicia con la presentación de la modelación de la aeronave, a continuación, se exponen los fundamentos teóricos del método de identificación utilizado, continuando con el diseño del control predictivo adaptativo y de la sintonización del controlador PID empleando la técnica de asignación de polos, finalmente, se presentan y analizan los resultados y las conclusiones.
2. MATERIALES Y METODO
2.1. Modelo de la aeronave
En el desarrollo del trabajo se utilizó el modelo matemático de un VANT del departamento de Aerotecnia de la Escuela Universitaria de Ingeniería Técnica Aeronáutica, analizado en [7]. En la fig.1. se muestran los tres ejes perpendiculares entre sí sobre los cuales una aeronave puede rotar, estos ejes son:
Eje Longitudinal (Eje x): se extiende desde la nariz hasta la cola del avión. El giro que se realiza sobre este eje se conoce como roll. Se controla con los alerones.
Eje Lateral (Eje y): se extiende de punta a punta de las alas del avión. El giro que se realiza sobre este eje se conoce como pitch. Se controla con el timón de profundidad o elevador.
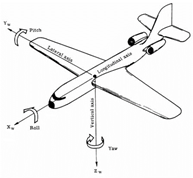
Fig. 1 Ejes de una aeronave. Tomado de [8]
Eje Vertical (Eje z): pasa por el centro de gravedad del avión, es perpendicular a los ejes transversal y longitudinal. El giro que se realiza sobre este eje se conoce como yaw. Se controla con el timón de dirección.
Las ecuaciones que describen el movimiento longitudinal y latero-direccional, son las siguientes:
2.1.1. Modelo longitudinal. Definido por la ecuación (1)
|
|
|
, 
y
son los coeficientes que relacionan la
resistencia aerodinámica y el empuje del UAV con respecto a
los cambios en la velocidad horizontal u, vertical w en el eje
X y en el eje Y respectivamente.
es el coeficiente que relaciona los cambios
en la resistencia aerodinámica producidos por cambios en el
timón de profundidad.
:
Ángulo de deflexión del timón de profundidad
,
, 
,
,
, 
,
y 
son
coeficientes que dependen entre otros factores de los
coeficientes que relacionan los cambios en la sustentación,
producidos por el cambio en la
dirección del aire desviado por la acción del ala del avión,
conocido como efecto downwash en cola.
Las variables de estado para el sistema se definen de la siguiente manera:
: Velocidad en x
: Velocidad en z
: Velocidad angular en y
: Angulo en y
La representación del modelo en variables de estado está dada por la ecuación (2) y propuesta en [7]
|
|
|
Con:
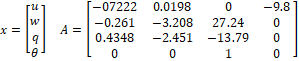
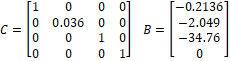
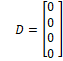
2.1.2 Modelo latero-direccional. Dado por la ecuación (3)
|
|
|
es el coeficiente que relaciona la
resistencia al movimiento horizontalmente del UAV, producida
en mayor parte por la cola vertical y en menor medida por el
fuselaje. 
son los coeficientes que dan la velocidad lateral
al presentarse un cambio en la posición de los alerones y
timón de dirección respectivamente. 
y 
Ángulos de deflexión de alerones y timón de
dirección respectivamente. 
y 
y 
son pares de coeficientes que dependen de los
momentos de inercia y relación de la resistencia a rotar en
torno al eje X y en eje Z del VANT producida por el diedro del
VANT y la cola vertical y el diedro del VANT y las alas
respectivamente.
y 
son coeficientes que dependen de los momentos de
inercia y de la relación del momento de roll y de yaw
producido por la sustentación al haber una perturbación en el
régimen de yaw.
y 
; 
y 
son
pares de coeficientes que dependen de los momentos de
inercia y de los coeficientes que proporcionan el roll
y el yaw al presentarse un cambio en la posición de
los alerones y del timón de dirección respectivamente. Para
las entradas correspondientes a alerones y timón, se definen
las siguientes variables de estado:
v: Velocidad en y
p: Velocidad angular en x
r: Velocidad angular en z
φ: Angulo en x
La representación en el espacio de estado para el sistema se da en la ecuación (4), según [7]
|
|
|
Con:
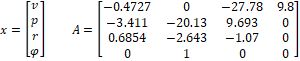
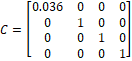
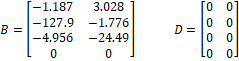
2.2. Identificación en línea del modelo
De acuerdo con [8], la técnica del control adaptativo requiere estimar en línea los parámetros de la planta para calcular el controlador correspondiente. Una de las estrategias para la identificación paramétrica en línea, se basa en el método de mínimos cuadrados [9]. En este caso, se asume que la función de transferencia del modelo este dado mediante la ecuación (5),
En donde 
es
la entrada e 
es
la salida.
El sistema dado por la ecuación (5) queda descrito mediante la ecuación en diferencias (6):
Que corresponde a un modelo autorregresivo de promedio móvil con variable exógena, ARMAX, por sus siglas en inglés y en él se debe estimar el vector de parámetros:
Utilizando un conjunto de 
pares
de mediciones de entrada–salida del sistema (siento el
número de datos):
A causa del error que se puede presentar en la medición, la ecuación (6) se transforma en:
La ecuación (9) se puede escribir en la forma:
En donde es
el vector de parámetros definido en la ecuación (7) y:
El vector debe
minimizar la suma de los cuadrados del error, es decir,
minimizar la función:
En donde 
es
una matriz diagonal. Minimizando la ecuación (12)
resulta:
En [9] se considera que
el factor de peso puede
tomar la forma dada en la ecuación (14):
A partir de las ecuaciones (12), (13) y (14) se obtiene:
En donde:
Reemplazando 
por
y
con 
se
obtienen las ecuaciones en diferencias recursivas que permiten
estimar los parámetros del sistema. Para iniciar la
identificación se puede hacer 
.
En donde 
es
un escalar de valor elevado 
,
luego se obtienen los valores estimados para
y
.
2.3. Control predictivo generalizado
El control predictivo generalizado (GPC), es una estrategia que hace uso explícito del modelo del sistema a controlar para calcular una secuencia de acciones de control futuras de modo que se minimice una función de costo cuadrática que mide, por un lado, la diferencia entre la salida predicha y el valor referencia establecido hasta el horizonte de predicción y por otro, el esfuerzo de control necesario para obtener dicha salida [10]. El GPC utiliza un modelo autorregresivo de media móvil integrado, (CARIMA) [11], dado por la ecuación (21):
En donde:
El último término de la ecuación (21), se puede escribir en la forma:
Para simplificar se asume:
, B
, 
, 
De la ecuación (22) se obtiene:
Haciendo:
y despejando 
:
Multiplicando
la ecuación (21) por 
se obtiene:
De la ecuación (25) resulta:
Haciendo
se obtiene:
Los
polinomios 
y 
se calculan recursivamente, con la ecuación (24) de
manera que los valores en el paso 
son función de los del paso anterior.
La
mejor predicción de 
se obtiene cuando 
, por lo tanto:
La ecuación (28) se puede escribir matricialmente así:
Donde:
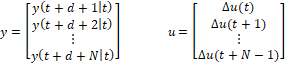
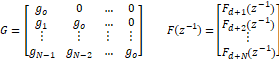
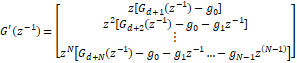
En la
ecuación (29) los dos últimos términos dependen solo de
valores pasado entonces, se pueden agrupar en un solo término
, dando lugar a:
La función de costo a minimizar propuesta para el control predictivo generalizado es, según [11]:
En donde:
: Predicción de la salida 
pasos adelante.
: Horizonte mínimo de predicción.
: Horizonte máximo predicción.
: Horizonte de control.
: Trayectoria futura de referencia.
: Secuencias de ponderación del error
: Secuencias de ponderación del esfuerzo de
control. En este caso 
para trabajar con el error calculado y se toma como parámetro de diseño.
Reemplazando la ecuación (30) en la ecuación (31):
Minimizando
la ecuación (32) con respecto al esfuerzo de control resulta:
Como en
el instante 
solo se aplica al sistema de control la
salida 
, solo interesa el primer elemento del vector así, la ley de control es:
Siendo
, la primera fila de 
2.4. Control PID por asignación de polos.
Para sintonizar el controlador PID se utilizó el
método de asignación de polos presentado en [12] y [13]. Si 
representa el proceso y 
el controlador, la función de transferencia en
lazo cerrado es:
La ecuación del controlador PI se puede escribir como:
Si se asignan polos en 
la ecuación característica del sistema en
lazo cerrado cumple con:
Resolviendo la ecuación (37) para 
y 
resulta:
En donde:
Para un controlador PID ideal:
con:
La función de transferencia del controlador PID discreto equivalente está dada por:
En donde:
Periodo de muestreo 
3. RESULTADOS
3.1 Modelos estimados
Para estimar los modelos correspondientes a la dinámica de los ángulos, se empleó el algoritmo de mínimos cuadrados recursivos (RLS) en línea. En la fig.2, fig.3 y fig.4 se presentan las respuestas de los datos generados por el modelo original y los datos estimados por el modelo ARMAX obtenido. De ellas se deduce que los modelos estimados describen adecuadamente la dinámica de los modelos iniciales tomados de la planta propuesta en la literatura para la aeronave y presentada en las secciones 2.1.1 y 2.1.2.
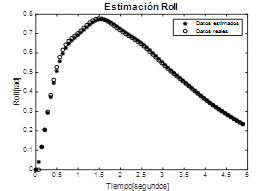
Fig. 2 Modelo estimado – Roll
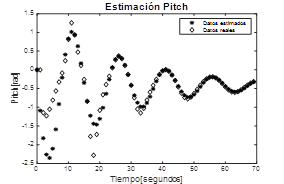
Fig. 3 Modelo estimado -Pitch
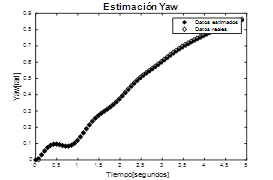
Fig. 4. Modelo estimado – Yaw
En la tabla 1 se presentan los modelos estimados para los ángulos correspondientes al roll, al pitch y al yaw.
Tabla 1 Modelos estimados
|
Roll |
|
|
Pitch |
|
|
Yaw |
|
3.2 Controladores predictivos
El proceso de identificación del sistema y cálculo de los parámetros de los controladores predictivos se realizó en línea en la plataforma Matlab®. La fig.5. y la fig.6. corresponden al diagrama en Simulink® utilizado para simular los controladores estimados y obtener la respuesta del sistema con el fin de observar el comportamiento de los ángulos de pitch, roll y yaw al aplicarle una perturbación de tipo escalón.
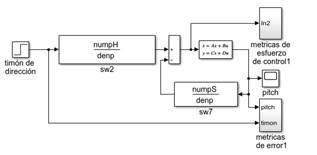
Fig. 5. Sistema Pitch con controlador predictivo
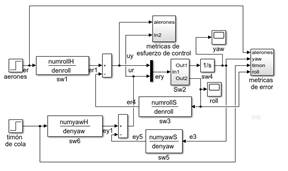
Fig. 6 Sistema roll - yaw con controlador predictivo
En la tabla 2 se presentan las funciones de transferencia de los controladores predictivos estimados en línea para cada uno de los ángulos.
Tabla 2. Controladores Predictivos estimados
|
|
|
|
|
Roll |
|
|
|
Pitch |
|
|
|
Yaw |
|
|
En la fig. 7, se muestra la respuesta del roll cuando se coloca como referencia un ángulo de 0.1 rad. Se observa que el sistema alcanza el valor de referencia, pero con cierta oscilación y alto sobreimpulso, en t=25 s se aplica una perturbación al sistema, se aprecia el efecto inicial de la misma sobre la respuesta del proceso y la forma como el control la elimina. La fig. 8 representa la respuesta del ángulo de pitch cuando la referencia corresponde a un ángulo de 0.1 rad, al igual que en el caso anterior, se alcanza el valor de referencia, pero con un sobreimpulso considerable, en t=25 s se aplica una perturbación, se observa el efecto de ella y la forma como el sistema de control la elimina. Finalmente, la fig.9 corresponde a la respuesta del ángulo de yaw cuando el ángulo de referencia es de 0.1 rad, el sistema alcanza el valor deseado y presenta buena respuesta en presencia de perturbaciones. En todos los casos, el comportamiento de la ley de control hace que la aeronave se estabilice en los valores de referencia y elimina las perturbaciones introducidas al sistema.
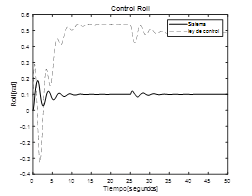
Fig. 7. Respuesta sistema Roll con control predictivo
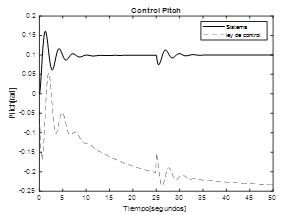
Fig. 8. Respuesta Pitch con controlador predictivo
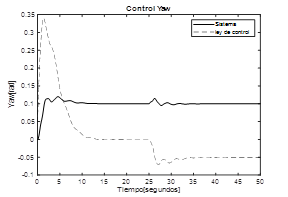
Fig. 9. Respuesta Yaw con controlador predictivo
3.3 Controlador PID por asignación de polos
Los controladores PID, se estimaron mediante la técnica de asignación de polos. Los polos dominantes se ubicaron teniendo en cuenta el tiempo de establecimiento y el coeficiente de amortiguamiento deseados para cada sistema en lazo cerrado. En la tabla 3 se presentan los parámetros de los controladores discretos calculados para los ángulos de roll, pitch y yaw.
Tabla 3 Controladores PID estimados
|
|
Entrada |
|
|
|
|
Roll |
Alerón |
10.735 |
-19.715 |
9.16 |
|
Timón |
427.73 |
-822.48 |
395.57 |
|
|
Pitch |
Timón dirección |
-150.42 |
289.34 |
-139.17 |
|
Yaw |
Alerón |
59.323 |
-116.65 |
57.349 |
|
Timón |
35.495 |
-69.772 |
34.291 |
La fig.10. corresponde al diagrama en Simulink® utilizado para obtener las respuestas del sistema con los controladores PID y al mismo tiempo, calcular el valor de las métricas utilizadas para la comparación del desempeño de los controladores.
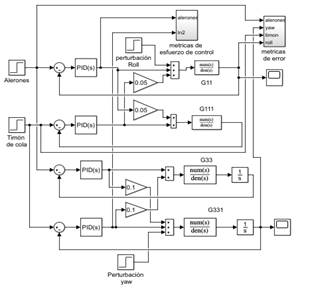
Fig. 10. Diagrama de controladores PID
En la fig.11. se presenta la respuesta del ángulo de roll al aplicarle una referencia de 0.1 rad, igualmente se observa que en t=25 s se aplica una perturbación al sistema, el controlador elimina su efecto y lo lleva nuevamente al valor deseado. En la fig.12. se observa el comportamiento del ángulo de roll cuando la referencia se coloca en 0.1 rad, su respuesta es estable y se ve muy poco afectada por la presencia de la perturbación introducida en t= 25 s., finalmente, en la fig.13. se ve la respuesta del ángulo de yaw, al igual que las anteriores, alcanza el valor de referencia y se recupera rápidamente en en presencia de perturbaciones.
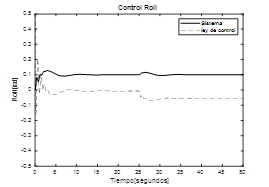
Fig. 11. Respuesta sistema Roll con control PID
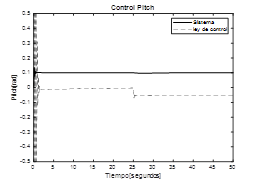
Fig. 12. Respuesta sistema Pitch con control PID
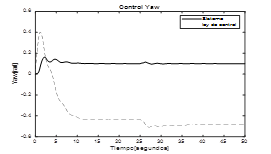
Fig. 13. Respuesta sistema Yaw con control PID
4. ANÁLISIS DE RESULTADOS
Con el fin de obtener una comparación cuantitativa del desempeño de los controladores predictivos y de los controladores PID sintonizados, se utilizaron métricas basadas en la integral del valor absoluto del error (IAE), la integral del error al cuadrado (ICE) y el Trabajo de la Variable Manipulada (TVM). Esta última se define como la integral del valor absoluto del cambio de la variable manipulada. En la tabla 4 y en la tabla 5, se presentan los valores estimados para cada uno de los criterios de comparación establecidos, al introducir un cambio en la referencia de cada uno de los ángulos. El IAE el ICE y el TVM se miden bajo las mismas condiciones para los controladores predictivos y para los PID. Se observa que, según estos criterios, la técnica del control predictivo presenta mejor desempeño que la del control PID.
En cuanto a la respuesta temporal se observa que, con los dos tipos de control, las respuestas son estables, muestran tiempos de establecimiento con diferencias poco significativas, error de estado estable igual a cero en todos los casos y regresan al valor de referencia ante las perturbaciones introducidas pero el control predictivo presenta, en general, mayor sobreimpulso.
Tabla 4 Métricas para los controladores predictivos
|
|
Roll |
Pitch |
Yaw |
|
IAE |
131.21 |
96.42 |
181.55 |
|
ICE |
2.87 |
3.52 |
7.51 |
|
TVM |
103.77 |
89.30 |
75.09 |
Tabla 5 Métricas para los controladores PID
|
|
Roll |
Pitch |
Yaw |
|
IAE |
870.80 |
149.63 |
1051.14 |
|
ICE |
22.91 |
3.475 |
21.28 |
|
TVM |
6808.9 |
1630.4 |
334.524 |
5. CONCLUSIONES
Al finalizar el trabajo, se puede concluir que se ha cumplido el objetivo de simular el modelo de la aeronave e implementar los sistemas de control predictivo adaptativo y PID en el entorno de Matlab®-Simulink® para controlar sus movimientos longitudinal y latero-direccional y estabilizarla ante cambios en el punto de consigna y en presencia de perturbaciones. Como aporte importante con respecto a otros trabajos, en los cuales solo se implementan controladores con parámetros fijos, en este trabajo se desarrolla un algoritmo de identificación recursivo que permite estimar, con gran precisión, los modelos discretos para cada uno de los ángulos que se controlan en el VANT, lo cual hace posible implementar en forma práctica diferentes algoritmos de control adaptativos.
Es importante destacar que el software de identificación y control desarrollado en la plataforma Matlab®-Simulink®, se programó de forma que se puede aplicar a cualquier modelo de VANT con solo ajustar los parámetros correspondientes.Las simulaciones realizadas permiten concluir que la estrategia de control predictivo adaptivo es una buena alternativa al control convencional y que genera un adecuado control sobre las variables, acorde con los requerimientos del sistema. Así mismo, la estrategia de control PID permitió controlar satisfactoriamente al sistema, mostrando la efectividad característica de este algoritmo de control convencional. Se hace notar que los algoritmos de control diseñados fueron probados en varios puntos de operación obteniendo los resultados esperados, es decir, un control preciso sobre las variables, de acuerdo con los requerimientos de proceso. A futuro, se pretende construir un prototipo de VANT, una vez se tenga el análisis económico que determine el costo total del proyecto y los beneficios socio-académicos como resultado de su implementación
6. Agradecimientos
A la institución universitaria de Envigado por la financiación del proyecto de investigación y al grupo sistemas e informática por el apoyo al desarrollo de la investigación.
7. Referencias Bibliográficas
|
[1] |
D. Hernández, «Modelado dinámico de aviones subsónicos a partir de herramienta de software.,» 2004. |
|
[2] |
F. M. O. Guerrero, «simulación y control de sistemas aéreos no tripulados utilizando inteligencia artificial,» Quito, 2013. |
|
[3] |
D. VIÚDEZ, «Sistema de control de vuelo optimizado adaptativo para una aeronave de ala fija,» 2013. |
|
[4] |
A. Cabrerizo, «Identificación de parámetros de modelo dinámico de un vehículo aéreo no tripulado,» 2017. |
|
[5] |
L. Solaque, «Modelado y control de un prototipo de aeronave no tripulada de ala fija,» Revista Politécnica, 2014. |
|
[6] |
S. Gutiérrez, «Modelado, simulación y control inteligente de uavs,» 2013. |
|
[7] |
O. V. Rovira, «Modelización de aeronaves no tripuladas con Simulink,» 2011. |
|
[8] |
M. José, «Conceptos básicos antes de subir a la cabina de tu avión virtual,» 2008. [En línea]. Available: http://blog.sandglasspatrol.com. |
|
[9] |
G. P. D. Franklin, Digital control of dynamic systems, 1994. |
|
[10] |
C. Bordons, «Control Predictivo: metodología, tecnología y nuevas perspectivas». 2015 |
|
[11] |
E. B. C. Camacho, «Model Predictive Control. Springer Verlag,» 1999. |
|
[12] |
J. Dulhoste, «Introducción al Control de Procesos para Ingenieros,» Mérida – Venezuela, 2013. |
|
[13] |
F. M. F. D. S. Vázquez, «An iterative method for tuning decentralized PID controllers,» Proceedings of the 14th IFAC World Congress, 1999. |
|
[14] |
T. Söderström, System Identification, London: Prentice Hall, 1989. |