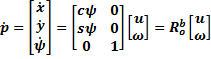Control de velocidad traslacional y orientación de un robot dedicado a agricultura de precisión
Leonardo Enrique Solaque Guzmán 1, Guillermo Sánchez Herrera 2, Adriana Riveros Guevara 3
1 Doctor en Ingeniería, Docente de planta, leonardo.solaque@unimilitar.edu.co
2 Ingeniero Mecatrónico, Asistente de investigación, 3 Magister en Mecatrónica, Docente ocasional.
1, 2,3 Universidad Militar Nueva Granada
RESUMEN
Diversas labores agrícolas pueden ser conducentes a fatiga o desencadenantes de enfermedades en el agricultor. Para la asistencia de estas tareas, se ha empleado la robótica como una posibilidad para minimizar los inconvenientes mencionados. Considerando lo anterior, la Universidad Militar Nueva Granada diseñó y construyó un robot llamado CERES, el cual realiza labores de remoción de maleza, fumigación, entre otros. Para que CERES pueda movilizarse en los cultivos siguiendo una trayectoria deseada, se debe asegurar el desplazamiento del robot con una velocidad traslacional y orientación específica, la cual se garantiza mediante el uso de controladores. El presente artículo muestra el diseño e implementación de controladores PID, para el seguimiento de la velocidad lineal y orientación, asegurando cumplir los tiempos de estabilización cuando el error tiende a cero, usando el criterio de SSV (Steady State Value), y señales de control admisibles por el Hardware del robot.
Palabras clave: Robot agrícola; Control; Modelado; Robótica
Recibido: 30 de Septiembre de 2018. Aceptado: 28 de Diciembre de 2019
Received: Septiembre 30, 2019. Accepted: December 28, 2019
Translational and rotational speed control for a precision agriculture robot
ABSTRACT
Various agricultural tasks can be conducive to fatigue or being triggers of diseases in farmers. For assistance of these tasks, robotics has been used as a possibility to minimize the aforementioned drawbacks. Considering the previous, the Universidad Militar Nueva Granada designed and built a robot called CERES, which performs tasks of weed removal, fumigation, among others. To ensure that CERES can move in crops following a desired trajectory, displacement of robot with a translational speed and specific orientation must be ensured, which is guaranteed using controllers. This article shows the design and implementation of PID controllers, for the tracking of linear speed and orientation, ensuring to meet a settling time when error tends to zero, using SSV (Steady State Value) criteria, and control signals admissible by the robot’s Hardware.
Keywords: Agricultural robot; control; modelling; robotic
Cómo citar este artículo: H. González, Y. Guerrero, “Translational and rotational speed control for a precision agriculture robot”,
Revista Politécnica, vol. 15, no.28 pp.9-19, 2019. DOI: https://doi.org/10.33571/rpolitec.v15n28a1
1. INTRODUCCIÓN
El crecimiento poblacional proyectado de 3 billones de personas para 2025 [1] implica grandes retos para el sector agrícola. En las últimas décadas el aumento de la productividad agrícola ha permitido reducir el porcentaje de población mundial en condición de desnutrición [2]. La intensificación de cultivos, la mecanización y la automatización son importantes para la productividad agrícola al incrementar la eficiencia, la precisión y la confiabilidad [3]. El uso de maquinaria inteligente puede aumentar significativamente la producción en cultivos convencionales que son actualmente trabajados manualmente por los agricultores [4]. La robótica agrícola requiere de trabajadores especializados y equipos tecnológicos, lo cual es atractivo para las nuevas generaciones, permitiendo frenar el continuo crecimiento de la edad promedio de los agricultores [5]. La robótica ha tenido grandes desarrollos en la industria, sin embargo, los ambientes complejos y con gran variabilidad en luminosidad, temperatura y humedad en ambientes de agricultura requieren de sistemas robustos para apoyar labores agrícolas de forma segura.
La robótica móvil y específicamente los robots autónomos permiten tomar decisiones y acciones sobre el cultivo en tiempo real, sin intervención humana; y su uso en labores repetitivas que requieren precisión es de gran importancia. Sin embargo, un vehículo cien por ciento autónomo en ambientes complejos y no estructurados aún está en desarrollo debido a las incertidumbres e impredecibles condiciones ambientales, entre otras. [6]. Apuntando en esta dirección, el grupo GIDAM adelanta la puesta a punto de un robot agrícola llamado ‘’CERES’’ dedicado a tareas de agricultura de precisión. Esta estructura cuenta con un sistema de remoción de maleza, un sistema para aplicación de nutrientes sólidos centralizado y un sistema de fumigación, orientándose a cumplir con estándares amigables con el medioambiente [7].
Con el fin de realizar la o las tareas principales de cuidado de cultivo (remoción de maleza, fumigación y abono), el robot debe cumplir con unos requisitos de movilidad y maniobrabilidad que permitan la realización de estas labores a lo largo del cultivo, el desplazamiento es comandado por controladores de bajo nivel de orientación y velocidad basados en el estado de la plataforma medidos por los sensores disponibles en ella. En [8] se desarrolla un robot con 4 ruedas de tracción y dirección en cada una para realizar siembra de trigo con precisión, evidenciando una tasa de siembra efectiva mayor al 90%. Un sistema de control de orientación es mostrado en [9] para el uso en invernaderos para la navegación del robot mediante marcadores. La autonomía también se ha probado mediante integración de vehículos comerciales, en [10] se modifica un carro de golf, incluyendo sensores de navegación y cámaras, para realizar navegación autónoma en los cultivos, evitando obstáculos.
En la sección 2 se presenta el sistema de locomoción del robot CERES, se desarrolla el modelado dinámico desde un enfoque Newton-Euler y Euler-Lagrange y se realiza el diseño de las leyes de control PID y finalmente la puesta en funcionamiento de estos controladores en el robot. En la sección 3 se presentan los resultados obtenidos en pruebas simuladas y reales. Finalmente, se presentan las conclusiones sobre el trabajo desarrollado y los trabajos futuros en dirección hacia un vehículo autónomo para labores de agricultura de precisión.
2. MATERIALES Y MÉTODO
En esta sección se realiza el modelado cinemático y dinámico del robot CERES, posteriormente se plantean las leyes de control y se detalla la implementación de estas en el prototipo real.
La plataforma CERES ha sido diseñada al interior del grupo GIDAM (Grupo de investigación y Desarrollo de Aplicaciones Mecatrónicas) del programa de Ingeniería en Mecatrónica de la Universidad Militar Nueva Granada. Con esta se busca mejorar la calidad de la vida de agricultores y aportar en los procesos de agricultura de precisión. La Figura 1 presenta la plataforma CERES.
Fig.1. Imagen de CERES: Vehículo de tracción diferencial eléctrico (48V), con capacidad de carga de 100 Kg de abono sólido, 20 litros para fumigación y un sistema de remoción de maleza.
2.1 Modelado cinemático
En el modelo cinemático se busca referenciar los
movimientos de la plataforma a un marco general o global (
) [11] y [12],
partiendo de los movimientos locales que haga la estructura – marco robot (
). La Figura
2 ilustra el Robot en el espacio 3D con los respectivos sistemas coordenados.
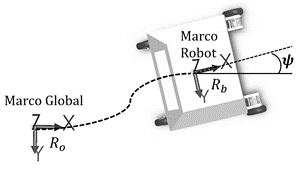
Fig.2. Marco global, marco local-robot y trayectoria que une los marcos global y local
Asumiendo que el Robot se desplaza a una velocidad
traslacional 
, y
rotacional 
en el marco
local (), se pueden
encontrar las velocidades que se reflejan en el sistema coordenado global (). Denotando 
como la
posición (
, 
) y
orientación (
) del robot
en el espacio , se encuentra
que la relación entre las velocidades en cada marco referencial están dadas por
la Ecuación 1: Transformación de a , siendo 
y 
.
|
|
(1) |
Cabe resaltar que las velocidades en 
a partir de
las velocidades en el sistema global son determinadas por 
. Es de notar
que el sistema impone restricciones no holonómicas representadas por la
ecuación 
.
2.2 Modelado dinámico por Newton-Euler y Euler Lagrange
La teoría de modelado por Newton-Euler se basa en los principios físicos de los elementos. La dinámica del sistema se enmarca por la Ecuación 2.
|
|
(2) |
Donde 
es la masa
del Robot, 
la inercia
del sistema, 
la fuerza y 
el par,
ambos proporcionados por el contacto de cada llanta y el suelo (ver Figura 3).
Donde es el
desplazamiento traslacional y 
el
desplazamiento rotacional u orientación.
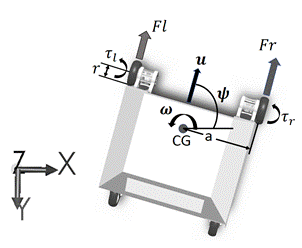
Fig.3. Modelo del sistema con las fuerzas y velocidades del sistema.
La Figura 3, permite identificar el centro de gravedad –
CG, lugar donde se realiza la sumatoria de todas las fuerzas y pares. Así, la
fuerza creada por cada llanta es proporcional al par creado por cada motor (
, donde 
es el radio
de la llanta). Llevando estos al CG, se tiene las relaciones que plantea la
Ecuación 3, que muestra las relaciones físicas asociadas al movimiento
rotacional.
|
|
(3) |
Donde
y 
son las
velocidades tangenciales de la llanta derecha e izquierda, respectivamente, y a
es la distancia medida desde la llanta al centro de gravedad.
La teoría de Euler-Lagrange permite construir la ecuación
dinámica, soportada sobre el Lagrangiano 
, que
a su vez se construye con la energía cinética 
y la energía
potencial .
Generalmente este enfoque complementa o suple el modelado por Newton-Euler.
Para el caso, permite completar dinámicas asociadas a la geometría de la
estructura y sus dimensiones (datos medidos en sistema físico o en el modelo
CAD). Asumiendo que existen coeficientes de fricción idénticos en las dos
llantas y una inercia debida al ensamble llanta-motor, se usa Ecuación 4 para
la determinación de la dinámica del sistema por el modelo Euler-Lagrange.
|
|
(4) |
Definiendo la energía cinética total como la suma del
aporte individual de la estructura en desplazamiento traslacional (
) y
rotacional (
),
y la energía cinética de las llantas (
), y la
energía potencial cero (
), el
Lagrangiano obtenido es 
. Después de
realizar operaciones matemáticas y aplicando la Ecuación 4, la dinámica del
robot CERES queda descrita por la Ecuación 5.
|
|
(5) |
Donde:
|
|
|
|
|
|
Adicionalmente, 
es el
coeficiente asociado a la fricción de las llantas y el terreno donde se
desplace el robot. Los pares 
y 
son los
generados por los motores y no siempre es inmediato encontrar la dinámica
propia debida al manejador de potencia Vector 300 de 48 Voltios y el motor
HPM5000B de 5KW del fabricante Golden motors, más información en [13]. Factores
como poca información sobre la caracterización de los motores o información
respecto a los manejadores de potencia (driver’s), hacen que para completar el
modelo se piense en una identificación de esta dinámica desde el voltaje de
entrada al manejador de potencia, hacia el par y/o velocidad tangencial de cada
una de las ruedas, lo cual se describe en la subsección 2.3.
Cabe resaltar que los valores de los coeficientes asociados al prototipo y que son necesarios para la simulación, son determinados desde el CAD del robot (ver Tabla 1).
Tabla 1. Coeficientes del sistema
|
Descripción |
Parámetro |
Valor |
|
Masa |
|
530Kg |
|
Inercia |
|
47*10^9 Kg*m2 |
|
Inercia de la llanta |
|
219*10^6 Kg*m2 |
|
Distancia centro de gravedad a llanta (lateral) |
|
1.2m |
|
Radio de la llanta |
|
0.28m |
2.3 Identificación de la dinámica de los manejadores de potencia y los motores a la velocidad tangencial
Sobre el principio que un motor DC tiene por entrada un
voltaje (
) que es
proporcional a la corriente que circula sobre él, y que la corriente es
proporcional al par (
) generado
por el motor DC, se puede establecer una proporcionalidad entre el voltaje de
entrada al manejador de potencia del motor HPM5000b de 5KW y el torque
generado. Así, la velocidad rotacional queda establecida por la señal de
entrada al motor. De esta manera, se plantea un modelo de identificación para
la dinámica de los motores eléctricos instalados en la plataforma CERES.
Como suele pasar, el bajo conocimiento o descripción de la dinámica asociada a los motores y el manejador de potencia, no es fácilmente determinada a partir de la información de los fabricantes, por tanto, se decidió hacer una identificación de esta dinámica e integrarla al modelo de la Ecuación 5.
Basado en las técnicas de identificación paramétrica, se
decidió colocar escalones de entrada, al sistema visto desde los manejadores de
potencia de los motores hasta la velocidad tangencial (
). Dentro de
este contexto se asumieron algoritmos de adaptación paramétrica de mínimos
cuadrados (por brevedad del articulo y no ser el tema central del mismo, se
remite al lector interesado consultar [14], [15] y [16]).
Luego de aplicar señales pseudoaleatorias (PRBS Pseudo Random Binary Sequences) al modelo y adquiridos los datos de la salida del sistema, se pasaron a un algoritmo de estimación paramétrica como mínimos cuadrados recursivos (RLS Recursive Least Squares), dando por resultado un sistema de primer orden, suficientemente representativo (con % de 94 de similitud). Las ecuaciones que relacionan el modelo para el motor derecho e izquierdo son presentadas por la Ecuación 6 en Velocidad angular de la llanta (rad/s) como función del Voltaje de entrada (V).
|
|
(6) |
Donde 
es ganancia
del sistema,
voltaje de
entrada al manejador de potencia y 
constante de
tiempo del sistema, los valores identificados se detallan en la Tabla 2.
Tabla 2. Parámetros identificados de los motores
|
Parámetro |
Valor |
|
|
35.8 |
|
|
42.1 |
|
|
0.94 |
|
|
1.08 |
2.4 Diseño de Leyes de Control
Para el modelo descrito por la Ecuación 5 y la Ecuación
6, se tiene que las dinámicas dominantes asociadas a la geometría de la
plataforma, obedecen a los términos 
y 
, puesto que
los términos 
y 
se
encuentran sobre el 13% del valor total. Esto indica que se pueden asumir las
velocidades de cada llanta sin tener acoples con la dinámica de la otra, todo
en el marco de las velocidades a las que se desplazará la estructura (0.7 m/s
para la velocidad lineal y 0.3 rad/s para la velocidad angular). Lo anterior
hace que la Ecuación 5 y 6 pueda ser reescrita como se presenta en la Ecuación
7 mostrando las dinámicas independientes.
|
|
(7) |
Donde
y 
engloban
todas las ganancias de los subsistemas o ganancias no modeladas.
Partiendo de la Ecuación 7, se propone un control PID, tal que permita estabilizar la velocidad traslacional y la orientación (recordar que son función de las velocidades angulares de las llantas). Sobre la base de tener un polinomio de Hurwitz, se establece la dinámica en lazo cerrado deseado (respetando la dinámica natural del sistema, tal que no realice esfuerzos grandes en la señal de control y por consecuente no se transmitan a los motores). En la Ecuación 8 se muestran los controladores planteados.
|
|
(8) |
Donde
y
, siendo 
y 
los valores
deseados de la velocidad traslacional y orientación, respectivamente. Cabe
recordar que la velocidad traslacional medida es 
.
Los valores de las constantes del controlador son presentados en la Tabla 3.
Tabla 3. Ganancias de los controladores
|
Ganancia |
Valor |
|
|
0.8 |
|
|
0.4 |
|
|
0.0 |
|
|
1.1 |
|
|
0.65 |
|
|
0.0 |
De la relación presentada en la Ecuación 3, 6 y 8, se determinan voltajes que cada motor debe tener para cumplir los objetivos.
Para la prueba de los controles, se programaron las ecuaciones asociadas a la cinemática, dinámica y control dinámico, bajo el esquema mostrado en la Figura 4.
Es de notar que el diseño está realizado en el dominio del tiempo continuo y la implementación se hizo en el domino del tiempo discreto. Para la discretización se partió de la selección del tiempo de muestreo del sistema (tm=1/20), tomando como partida que el sistema se estabiliza en 5s, con un tiempo de respuesta de 1s. Sobre el criterio de tener 20 veces el tiempo de muestreo en el tiempo de respuesta, se seleccionó una frecuencia de trabajo en el cálculo de la señal de control de 20Hz.
Sabiendo que el método de discretización ‘ZoH -retenedor de orden cero’ presenta equilibrio en respuesta temporal y frecuencial, se seleccionó para realizar la discretización de las leyes de control.
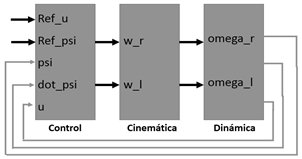
Fig.4. Esquema de simulación para prueba de modelo y controladores.
2.5 Puesta en Funcionamiento de los controladores
La integración y prueba de los controladores se realizó con el uso del entorno modular ROS (Robot Operating System), el cual permite la modularidad de los diferentes sensores y actuadores.
ROS provee una capa de comunicación funcionando en sistemas operativos Linux y grupo de computadores heterogéneo (Ej.: Computador y uno o varios sistemas embebidos). Entre sus características más relevantes está el brindar comunicación de igual a igual (peer to peer), puede ser programado tanto en C++ como en python y ejecutar estos programas provenientes de diferentes lenguajes en un mismo proyecto. ROS cuenta con herramientas para facilitar la visualización, supervisión de tiempos de ejecución e integración de diferentes componentes. Finalmente, ROS es de código abierto bajo la licencia BSD y cuenta con una amplia comunidad, lo cual facilita la corrección de errores y el soporte. Los detalles de su concepción pueden ser consultados en [17] y gran cantidad de tutoriales oficiales están disponibles en www.ros.org.
El nodo principal de ROS puede ser ejecutado en un sistema embebido o computador y conectado a hardware vía Ethernet, serial u otro sistema de comunicación. Los dispositivos en la red pueden adquirir información, procesarla y publicar una acción, todo lo anterior puede ser ejecutado usando nodos de hardware o software conectados.
Dentro del esquema de control de la plataforma, se tiene un planificador y un control de seguimiento de trayectoria, denominado control de alto nivel. Estos proporcionan las referencias para los controles de la velocidad traslacional y orientación denominados controles de bajo nivel, la Figura 5 muestra el esquema de control contemplando el seguimiento de trayectoria. Así, el presente artículo se centra en la implementación de los controles de bajo nivel, los cuales, se programaron en un Arduino Mega el cual se conecta por comunicación serial al computador principal que corre el nodo principal de ROS. En esta subsección se describe el hardware utilizado y el flujo de datos para la prueba de los controladores diseñados.
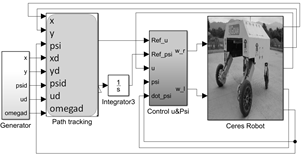
Fig.5. Esquema de control de seguimiento para la plataforma Ceres
La Figura 6 permite visualizar el hardware utilizado para la experimentación, los actuadores del sistema de control son los motores eléctricos del robot CERES acoplados a llantas rin 14 de un automóvil convencional, la sensórica corresponde a la unidad de medida inercial IMU Spatial Navigation la cual integra un GPS y permite conocer los estados del robot.
El procesamiento es realizado por un computador portátil donde se ejecuta el nodo principal de ROS y un Arduino Mega que permite recibir comandos por medio de mensajes de ROS y enviar las señales de control (voltajes) a los motores, para esto se realiza una etapa de optoacople entre los manejadores de potencia de los motores, que reciben la señal de control, y el Arduino. Con el propósito de realizar desplazamientos del robot pre y post experimentación, se añade un radio control que permite el desplazamiento manual de CERES
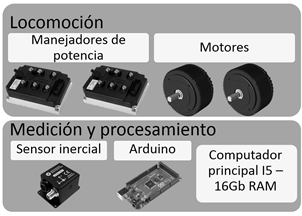
Fig.6. Hardware utilizado
En la Figura 7 se puede observar las velocidades de comunicación para los elementos principales del sistema y las variables enviadas. Esto se realiza programando un nodo de ROS, que se ejecuta en el computador, adquiere la información de la IMU (la cual implementa un filtro de Kalman sintonizado por el fabricante), esta información se pre procesa para ser enviada al nodo relacionado al Arduino. El Arduino recibe la información de referencias y mediciones actuales para calcular y enviar la señal analógica al manejador de potencia, publicando estos valores al nodo principal para el registro de datos.
Para la experimentación, se realiza el desplazamiento del robot a una zona amplia, y se envían comandos tipo paso en posición angular y velocidad lineal desde el radio control o desde un nodo de ROS que publica estos comandos pre-programados.
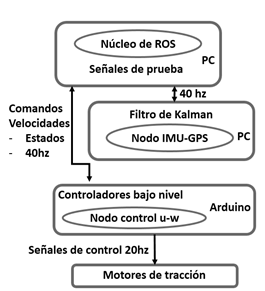
Fig.7. Esquema de comunicación de ROS programado en el computador embarcado y sistema embebido
3. RESULTADOS
En
esta sección se presentan las curvas de respuesta del sistema en simulación y la
implementación del mismo control sobre el prototipo. El criterio de diseño del
control se realizó sobre la base de lograr tener error de estado estable cercano
a cero (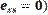
, con tiempos de
establecimiento similares a los del sistema en lazo abierto (aplicando el
criterio SSV) y una repuesta cercana a ser críticamente amortiguada (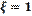
), cuando se tienen por
entrada referencias tipo escalón.
3.1 Resultados en simulación
La
simulación cuando el vehículo sigue una velocidad traslacional de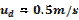 
y una orientación de 
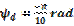son presentados en las
Figuras 8 y 9. La Figura 8 muestra que las señales de salida en velocidad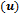 
y orientación 
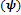se aproximan al escalón
de referencia en tiempos cercanos a los de lazo abierto, que para el caso, la
velocidad lineal es cercano a los 2.5s y el tiempo para la orientación sobre
los 8s. Cabe resaltar que para la determinación de estos tiempos se usa el
criterio de asentamiento (SSV), que determina estar alrededor del valor final,
sobre una franja del 10%.
En la Figura 9 se observa que las señales de control (para motor derecho y motor izquierdo) se encuentran entre los rangos permitidos por los manejadores de potencia de los motores.
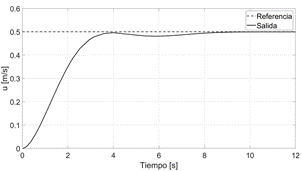
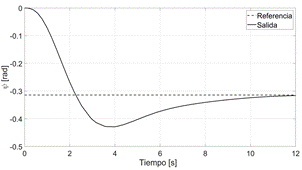
Fig.8. Seguimiento de referencias en velocidad y orientación – pruebas en simulación
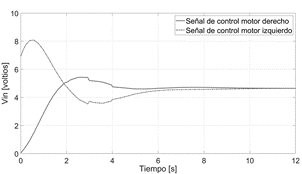
Fig.9. Señales de control acordes a los voltajes permitidos por el manejador de potencia – pruebas en simulación.
3.2 Resultados experimentales
Luego
de tener a punto la electrónica y la programación de los algoritmos de control,
se procedió a la realización de experimentaciones con señales de referencia
iguales a las usadas en la simulación (
, y 
).
Sin perder generalidad de la prueba, la experimentación se llevó a cabo sobre una superficie de cemento. Lo anterior se soporta sobre la base de tener una medición de las señales con una central inercial que realiza fusión sensórica con Filtro de Kalman.
La Figura 10 presenta el seguimiento a las referencias, tomando las salidas desde la información que entrega la Central Inercial embarcada (velocidad y orientación), evidenciando un seguimiento de las señales deseadas.
El tiempo de estabilización de la velocidad traslacional del sistema real se logra cercano a los 2s. La orientación del robot alcanza la referencia sobre los 6s.
Estos tiempos son próximos al de la experimentación en simulación. Las diferencias pueden ser atribuidas a dinámicas que en la identificación dieron más lentas, cuando en la realidad son más rápidas.
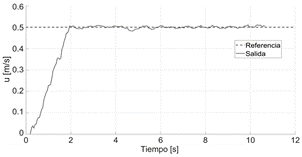
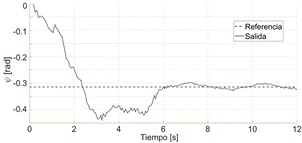
Fig.10. Seguimiento de referencias en velocidad y orientación – pruebas reales.
La Figura 11 muestra los voltajes aplicados a los manejadores de potencia de los motores. Presentan una respuesta parecida a los resultados de simulación a nivel dinámico. Los valores iniciales cambian por las condiciones en el entorno simulado y las condiciones iniciales en el entorno real.
En resumen, los supuestos para el desarrollo de los controles y su codificación en un entorno de programación de robots como ROS, aseguran un desempeño aceptable a nivel de similitudes de dinámica en resultados simulados y reales.
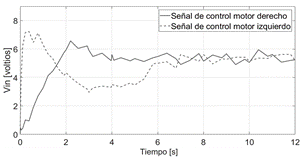
Fig.11. Señales de control acordes a los voltajes permitidos por los manejadores de potencia – pruebas reales.
4. CONCLUSIONES
Bajo el direccionamiento de soportar labores de agro que permitan la eficiencia de la producción y aporte a la minimización de riesgos en el agricultor, se enmarcan los aportes tecnológicos que permitan soportar la agroindustria. Así, desde la implementación de plataformas como la que se menciona en este documento, se abre un campo de acción desde la robótica para la agroindustria.
En la búsqueda de la autonomía de la plataforma robótica CERES, se realizó un estudio de su modelado desde una perspectiva cinemática y dinámica, encontrando que algunas de las partes del modelo no son fácilmente determinadas a partir del CAD de la estructura o de la información de los fabricantes de los componentes instalados en el robot. Por esto, el uso de técnicas de identificación, permiten complementar el modelo matemático, para la determinación de las dinámicas del modelo que no son determinadas de manera directa desde la teoría.
En un contexto de buscar modelos afines, bajando complejidad a los controladores, y a su vez teniendo en cuenta las restricciones en el movimiento de la plataforma, acordes a los desplazamientos reales que hace el robot, se logran establecer modelos suficientemente representativos de la dinámica de CERES y a partir de estos, diseñar los controles tipo proporcional, integral, y derivativo, calculándolos desde el diseño tradicional de PID y garantizando estabilidad por la teoría de Hurwitz.
Los resultados a nivel de simulación validan la correspondencia con los valores reales permitidos sobre la estructura. Así, las pruebas que se presentaron muestran un cumplimiento del seguimiento de las referencias en velocidad traslacional y orientación, encontrándose en los valores permitidos por los manejadores de potencia de los motores y la dinámica propia del robot real.
Desde un análisis de estabilización por el criterio SSV, se tiene que los diseños y pruebas de los controles, tanto en simulación como en el prototipo real, mostraron corresponder a estabilizarse en tiempos cercanos a los que presenta el sistema en lazo abierto y con señales de control según los límites que los manejadores de potencia de los motores soportan.
Si bien las pruebas se realizaron sobre una superficie de cemento, se establece que las señales con las que se realimentan los controladores, son aportadas por una central inercial que realiza fusión sensórica sobre la base de un filtro de Kalman. Lo anterior permite minimizar problemas de odometría que normalmente son presentados en estructuras con configuraciones similares a las de CERES y que son extrapoladas a superficies con deslizamiento.
La integración a la plataforma del desarrollo presentado se realizó sobre la base de la modularidad, integrando mediante hilos dedicados a la lectura de sensores, el cálculo de la señal de control, y otros dedicados a dialogar con los actuadores del robot, todos programados en el entorno ROS.
Un paso siguiente para el acondicionamiento de la plataforma CERES en las labores del agro, donde requiera navegar en un cultivo siguiendo los surcos o la trayectoria referenciada por el agricultor, es el desarrollo de controles de seguimiento de una trayectoria dada, es decir cerrar el lazo de control en una jerarquía superior a los controles presentados aquí (controles de bajo nivel).
5. AGRADECIMIENTOS
Este trabajo es soportado por el proyecto INV-ING-2637, titulado ‘Aproximación a la Autonomía de una plataforma robótica dedicada a labores de agricultura de precisión’, financiado por la Vicerrectoría de Investigaciones de la Universidad Militar Nueva Granada en Bogotá-Colombia.
6. Referencias Bibliográficas
[1] World Population Prospects - Population Division - United Nations, Population.un.org, 2018. [En línea]. Disponible en: https://population.un.org/wpp/. [consultado el 29 de Septiembre de 2018].
[2] Goal 2: Zero hunger UNDP, UNDP, 2018. Disponible en: http://www.undp.org/content/undp/en/home/sustainable-development-goals/goal-2-zero-hunger.html. [consultado el 29 de Septiembre de 2018].
[3] Q. Zhang, Opportunity of Robotics in Specialty Crop Production, IFAC Proceedings Volumes, vol. 46, no. 4, pp. 38-39, 2013.
[4] C. Xia, L. Wang, B. Chung and J. Lee, In Situ 3D Segmentation of Individual Plant Leaves Using a RGB-D Camera for Agricultural Automation, Sensors, vol. 15, no. 8, pp. 63-79, 2015.
[5] Aravind, Krishnaswamy R., Purushothaman Raja, and Manuel Pérez Ruiz. Task-based agricultural mobile robots in arable farming: A review. Spanish Journal of Agricultural Research 2017.15 (1), 2017.
[6] R. Xiang, H. Jiang and Y. Ying, Recognition of clustered tomatoes based on binocular stereo vision, Computers and Electronics in Agriculture, vol. 106, pp. 75-90, 2014.
[7] PROVISIONAL AGREEMENT RESULTING FROM INTERINSTITUTIONAL NEGOTIATIONS, Europarl.europa.eu, 2017. Disponible en: http://www.europarl.europa.eu/RegData/commissions/agri/inag/2017/11-21/AGRI_AG%282017%29613578_EN.pdf. [consultado el 29 de Septiembre de 2018].
[8] L. Haibo, D. Shuliang, L. Zunmin and Y. Chuijie, Study and Experiment on a Wheat Precision Seeding Robot, Journal of Robotics, vol. 2015, pp. 1-9, 2015.
[9] G. Gat, S. Gan-Mor and A. Degani, Stable and robust vehicle steering control using an overhead guide in greenhouse tasks, Computers and Electronics in Agriculture, vol. 121, pp. 234-244, 2016.
[10] Ball D, Upcroft B, Wyeth G et al. Vision-based Obstacle Detection and Navigation for an Agricultural Robot. Journal of Field Robotics. 2016; 33(8):1107-1130. doi:10.1002/rob.21644
[11] R. Siegwart and I. Nourbakhsh, Introduction to Autonomous Mobile Robots, 2nd ed. Cambridge: MIT Press, 2016.
[12] S. Tzafestas, Mobile Robot Control and Navigation: A Global Overview, Journal of Intelligent & Robotic Systems, vol. 91, no. 1, pp. 35-58, 2018.
[13] Golden Motor Canada. Disponible en: https://www.goldenmotor.ca/. [consultado el 29 de Septiembre de 2018].
[14] I. Landau, Digital control systems. London: Springer, 2007.
[15] L. Ljung, System identification, 2nd ed. Upper Saddle River, NJ: Prentice Hall PTR, 2012.
[16] K. Åström and B. Wittenmark, Computer-Controlled Systems, 3rd ed. Newburyport: Prentice Hall, 1996.
[17] Quigley, Morgan, et al. ROS: an open-source Robot Operating System. ICRA workshop on open source software. Vol. 3. No. 3.2. 2009.