1. INTRODUCCIÓN
Los plásticos derivados del petróleo cubren muchas necesidades del mundo moderno debido a su gran versatilidad [1]. Éstos pueden ser moldeados, extruidos y adaptados para satisfacer especificaciones técnicas particulares. También han permitido modificar el empaque de productos de una forma que ni el papel ni el metal han podido. Además, son más ligeros que las alternativas, lo que resulta favorable para el transporte y todos los aspectos logísticos relacionados con la economía a escala.
El crecimiento de la economía mundial y el consecuente aumento de la utilización de los materiales plásticos que implica, hacen insostenible a futuro un escenario sin alternativas a los combustibles fósiles [2]–[4]. Actualmente, la cantidad de residuos plásticos presentes en vertederos y rellenos sanitarios, principalmente los de alto peso molecular, constituyen un problema de contaminación ambiental debido a la tasa de degradación lenta del plástico y a la liberación de sustancias tóxicas. El tiempo de uso de los plásticos es relativamente corto por lo que se incrementa la necesidad de espacio para disponer de ellos en rellenos sanitarios y vertederos. Los aditivos que se suelen agregar a los plásticos, tales como colorantes y estabilizantes, pueden contaminar fuentes de agua subterránea. Los plásticos enterrados producen metano y pueden ser causa de explosiones. De otro lado, la combustión de desechos plásticos desprende dioxinas y furanos que son sustancias tóxicas y carcinogénicas [5].
La degradación térmica de polímeros es la descomposición química que presentan, debido a la ruptura de enlaces moleculares, como resultado de la aplicación de calor [6]. Se generan cambios a nivel de la estructura química y de las propiedades físicas como consecuencia de que los productos resultantes tienen una estructura molecular diferente y más simple que el producto original [7]. La degradación térmica de plásticos se puede clasificar en tres tipos: el primero corresponde a una degradación completa con ruptura de la cadena polimérica principal. En el segundo tipo, hay ruptura de segmentos laterales junto con la generación de productos volátiles y residuos carbonosos sólidos denominados char (nombre dado al residuo sólido final del proceso de pirólisis de polímeros en la literatura técnica tanto en inglés como en español). En el tercer tipo, están los polímeros con enlaces cruzados que tienen una mayor composición en residuos carbonosos que la presente en degradación de polímeros de segundo tipo, pero con menor cantidad de volátiles.
La pirólisis de residuos plásticos urbanos es la degradación térmica de polímeros mediante la aplicación de calor en una atmósfera sin oxígeno. La pirólisis constituye una alternativa para tratamiento de residuos plásticos urbanos (RPU) [8]. Es una alternativa viable que puede hacerse cargo del manejo de los desechos plásticos, permitiendo la valorización energética para generación de productos que tienen potencial comercial [9]–[11].
Los productos de la pirólisis de polímeros artificiales, al igual que de los naturales, son fracciones sólidas, líquidas y gaseosas. La fracción sólida del proceso está constituida por char. Las fracciones líquidas y gaseosas, se componen de hidrocarburos que pueden ser utilizados como combustibles o monómeros con alto valor comercial. En la primera década del siglo XXI, se implementaron plantas de pirólisis de plásticos no lavables y ya hay disponibles varias tecnologías para la implementación industrial del proceso. Para su realización, se utiliza un reactor en el cual se introduce la materia plástica prima.
Sin embargo, la pirólisis de residuos plásticos (RPU) es un proceso estocástico, no lineal, con parámetros distribuidos, con gran cantidad de factores de los que se desconoce una relación cuantitativa confiable, pero con gran influencia en el resultado final [12]. Los factores aleatorios que intervienen se encuentran desde la misma distribución molecular de las especies químicas, hasta la distribución aleatoria de los materiales que componen la materia prima [13]–[15]. El material utilizado en la pirólisis de RPU es una mezcla heterogénea de diferentes polímeros cuando proviene de depósitos que hacen acopio y aún más, cuando se toman de vertederos porque pueden incluir impurezas, tierra, desechos de comida, etc. En el interior del reactor, la distribución espacial y porcentual de los compuestos es difícil de predecir, si la materia prima no ha sido clasificada ni mezclada con criterio técnico.
Una herramienta para analizar la degradación térmica de polímeros y otras sustancias, es la termogravimetría (TG) [4]. Donde se dispone de equipos de medición sofisticados denominados termobalanzas para realizar pruebas experimentales y obtener curvas que muestran la reducción de masa de material inicial que se convierte en sustancias volátiles. Al interior de las termobalanzas, se cuenta con un ambiente controlado, donde el aire de la atmósfera se sustituye por algún gas inerte o incluso se puede operar en vacío. Los materiales sometidos a termogravimetría (TG), pueden ser expuestos a programas de temperatura isotérmico o isocinético. En el primer caso, la muestra para análisis se degrada a una velocidad de calentamiento constante (°𝐶/𝑚𝑖𝑛) y en el segundo caso, se mantiene constante la potencia térmica suministrada.
La cinética de la degradación térmica en la literatura clásica ha sido descrita ampliamente mediante ecuaciones no deducidas analíticamente sino por el estudio experimental del proceso [4] . Estas ecuaciones diferenciales son aproximaciones confiables en un rango de temperatura determinado, teniendo que recurrir a la segmentación del proceso. De esta forma, los parámetros cinéticos de una sustancia en particular y de mezclas en especial, son válidos en intervalos limitados de temperaturas y cambian de uno a otro. Las condiciones del proceso a nivel industrial, las características más relevantes de la materia prima y la forma en que son monitorizadas las variables involucradas, son radicalmente diferentes a lo que se contempla en condiciones de laboratorio. Los equipos para análisis termogravimétrico, cromatografía de gases y espectrometría de masas, funcionan en condiciones estériles, con contenedores hechos de material especial y controles electrónicos que garantizan la uniformidad de la transferencia energética. La muestra utilizada en laboratorio, tiene unas características de limpieza y pureza que no tiene la materia prima inicial. No es viable desde lo técnico ni desde lo económico, implementar instrumentación ni protocolos que repliquen las condiciones de laboratorio. La termogravimetría, sin embargo, proporciona unas condiciones cercanas a lo ideal, porque descarta los factores que hacen compleja a la pirólisis industrial de RPU. Entre otros: gradiente de temperatura nulo, material homogéneo, atmósfera inerte, ambiente interior esteril. Esto hace posible obtener parámetros clave para determinar la cinética química del proceso, que no son deducibles fácilmente mediante la monitorización de la operación de un reactor a escala piloto y menos aún a escala industrial.
En la pirólisis de RPU y en el análisis termogravimétrico, se somete un material a degradación térmica sin oxígeno. Pero, mientras la pirólisis es estocástica y no lineal, la termogravimetría es predecible. La pirólisis se puede considerar como una reacción paralela de degradación térmica de muchos materiales cuyo porcentaje en masa y en volumen es desconocido pero que individualmente son susceptibles de ser estudiados. Eso precisamente es lo que permite hacer la termogravimetría.
Este documento describe la utilización de un modelo dinámico discreto diferente a las alternativas clásicas que se han manejado para modelar la cinética de la degradación térmica. Aunque es una aproximación determinista de un proceso estocástico, se ha evaluado como un primer paso en la proyección del comportamiento dinámico del proceso de pirólisis de polietileno de baja densidad (LDPE). Se ha asumido que un reactor de pirólisis puede ser descrito razonablemente como un sistema que recibe potencia térmica, para aumentar su energía interna y presentando pérdidas debido a la diferencia de temperaturas entre el interior y el exterior. La combinación del modelo cinético de la degradación térmica con el modelo dinámico de un reactor básico simulado, permitió contar con una primera aproximación a las condiciones de operación de un futuro reactor a escala de laboratorio.
2. MARCO TEÓRICO
A. Descripción Global de la Pirólisis de RPU
El reactor es un depósito dentro del que se aloja la masa de materia prima para aplicarle potencia calórica que producirá un aumento de temperatura. El interior debe ser hermético para que el aire de la atmósfera no aporte oxígeno al proceso. Opcionalmente, es posible inyectar un gas inerte, como nitrógeno (N).
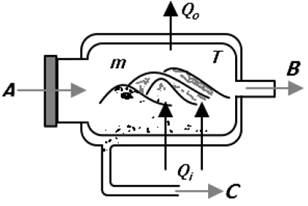
Fig. 1. Esquema del funcionamiento global de un reactor para pirólisis de RPU. Fuente: elaboración propia.
De acuerdo con la fig. 1, la materia prima se introduce por la compuerta A al inicio del proceso y mientras este permanece a temperatura ambiente 𝑇𝑒𝑥𝑡. La compuerta se cierra herméticamente y se extrae el aire inicial para sustituirlo con algún gas inerte. Se aplica calor al proceso mediante alguna fuente de potencia térmica, que puede ser un quemador a gas, resistencias calefactoras, microondas o con cualquier mecanismo de transferencia térmica.
La materia prima, compuesta por residuos plásticos, ingresa con una masa inicial 𝑚0 y a una temperatura 𝑇0. La aplicación de calor 𝑄𝑖 desde la fuente de flujo calórico, es una inyección de energía que se traduce en un incremento de la temperatura. El material absorbe calor hasta que el nivel de energía interna pueda alcanzar la energía de activación 𝐸𝑎 a partir de la cual empieza a producirse la reacción termoquímica. La degradación comienza con la ruptura de enlaces químicos y en diversas etapas, los materiales iniciales van dando origen a otros compuestos más simples. La materia sólida inicial, se convierte en fracciones líquidas y gaseosas que son extraídas a través de los conductos C y B respectivamente para recibir un tratamiento posterior.
La masa del material se reduce en la medida que ocurre la generación de los volátiles como consecuencia de la descomposición térmica. Siendo 𝑚, la masa instantánea del material sin volatilizar. Cada unidad de masa de material degradado es una unidad de masa de producto en cualquiera de sus fracciones, sólida, líquida o gaseosa. La fracción descompuesta, puede expresarse como:

Dónde:
𝑚0: masa inicial de material plástico.
𝑚: masa instantánea de material sólido no degradado.
𝑚𝑓: masa residual no degradable (char).
Para estudiar la reacción se analiza el comportamiento de la velocidad de degradación de masa descompuesta, de acuerdo a la razón de cambio de la misma con respecto al tiempo. Es decir, aplicando la derivada a la ecuación (1):
![]()
B. Cinética de la Degradación Térmica
La pirólisis, como un proceso inducido térmicamente, puede analizarse desde el perfil termogravimétrico, en términos de la razón de cambio de reacción con respecto al tiempo:
![]()
Donde 𝛼 es el grado de conversión, 𝑓(𝛼) es el tipo de reacción y 𝑘(𝑇) es la constante cinética, dependiente de la temperatura absoluta 𝑇. La cinética química de las reacciones de descomposición térmica en la literatura, ha sido aproximada mediante la ecuación de Arrhenius [16, p. 646] , incorporándola en (3):
![]()
Donde:
𝐸𝑎: Energía de activación en 𝐽.𝑀𝑜𝑙−1.
𝐴0: Factor pre-exponencial o factor de frecuencia.
𝑅: Constante universal de los gases 𝐽.𝐾−1𝑀𝑜𝑙−1.
La ecuación (4) no tiene una solución analítica y la determinación de las constantes cinéticas 𝐸𝑎, 𝐴0, requiere la aplicación de procedimientos basados en análisis numérico, que deben realizarse a velocidad de calentamiento constante, tales como: Ozawa, Flynn-Wall, Vyazovkin, entre otros [17].
Además, la función 𝑓(𝛼) puede tener una forma específica dependiendo de ciertas características del proceso.
C. Balance de Energía en el Reactor
El contenedor de los residuos plásticos, es un sistema al que se le aplica energía a una tasa determinada por la potencia térmica de la fuente calórica. Parte de esta energía que ingresa incrementa la energía interna del sistema, manifestándose con un incremento de la temperatura al interior del reactor. Una porción de la energía de entrada, escapa al exterior como una pérdida por fuga de calor a través de las paredes. El balance de energía, da origen a la siguiente expresión:
![]()
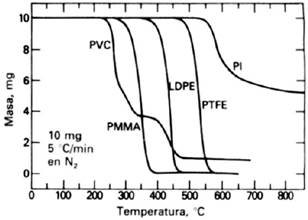
Fig. 2. Termograma de la degradación térmica de diferentes polímeros. Figura tomada del libro “Principios de Análisis Instrumental” [18], disponible en Internet.
Donde 𝜓 y 𝜌 representan características intrínsecas del sistema, relacionadas con la capacidad de absorción de energía y la conductividad térmica del material de la cubierta del reactor. 𝑇𝑒𝑥𝑡 es la temperatura media del ambiente cercano externo al reactor. El área en contacto con el exterior y el grosor de la cobertura son representados mediante los parámetros 𝑆 y 𝐿, respectivamente.
D. Análisis Termogravimétrico
Es una serie de técnicas de análisis instrumental en las que se hace un registro de la ganancia o pérdida de masa de una sustancia en función de la
temperatura [19, p. 207] . Una de las variantes es el análisis termogravimétrico dinámico, en la que la muestra es sometida a un programa de temperatura con una velocidad de calentamiento constante. Esta modalidad fue la que se utilizó como insumo para la deducción del comportamiento simulado del proceso de pirólisis.
En la figura 2, se puede apreciar la pérdida de masa en función de la temperatura de varios polímeros artificiales en una atmósfera de nitrógeno (N). La ecuación (4) puede utilizarse para describir el comportamiento del proceso pero es necesario aplicar ciertas restricciones. Entre otras, el resultado de la ecuación aplicada numéricamente a los datos de un termograma, es aproximado a partir del valor de temperatura donde se inicia la pérdida de masa sólida.
E. Planteamiento de la Hipótesis
Se propone una ecuación que relaciona la razón de cambio de la masa respecto a la temperatura:
![]()
Donde 𝐴, 𝑚𝑓, 𝑇𝑓𝑥(𝑇) y 𝜎, son parámetros que pueden determinarse a partir de los datos proporcionados por una termogravimetría dinámica. De esta forma, las ecuaciones (5) y (6) sirven como punto de partida de una simulación del proceso de pirólisis de residuos plásticos de un mismo polímero. La ecuación (6) puede representar mejor el comportamiento de la degradación térmica en un intervalo más amplio de temperaturas que la ecuación (4).
La ecuación (6) es una relación experimental propuesta tras realizar derivación numérica a los datos de la termogravimetría. No se encuentra en la literatura técnica porque es un aporte presentado en este trabajo por primera vez. La Figura 4, es la curva de tendencia que mejor se adapta a los resultados de esa derivación.
La degradación térmica de un polímero, como por ejemplo el polietileno de baja densidad (LDPE), sometido a análisis termogravimétrico, presenta una tendencia que se puede aproximar a la siguiente figura:
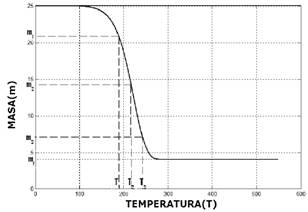
Fig. 3. Curva de tendencia aplicable a la degradación térmica de LPDE. Los datos en la gráfica son sólo de ejemplo y no corresponden a valores experimentales.
La razón de cambio de la masa respecto a la temperatura, arroja la siguiente tendencia:
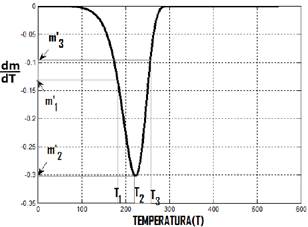
Fig. 4. Ejemplo de curva de tendencia de los datos de la variación de masa por degradación térmica de polietileno. Los valores mostrados en la gráfica son solo a manera de ejemplo.
La figura 4, es un ejemplo de la forma que puede tener una gráfica de 𝑑𝑚/𝑑𝑇 contra 𝑇. Tanto en la figura 3 como en la 4, se han ubicado arbitrariamente 3 puntos correspondientes a 3 temperaturas 𝑇1,𝑇2 y 𝑇3 con sus respectivas masas residuales 𝑚1,𝑚2 y 𝑚3 respectivamente. Además, en cada punto se puede determinar el valor numérico de las derivadas puntuales: 𝑚′1, 𝑚′2 y 𝑚′3 respecto a la temperatura 𝑇.
Los tres puntos que pueden seleccionarse arbitrariamente de la gráfica cuya tendencia muestra la figura 3 y los valores de las pendientes en estos mismos puntos (Figura 4), son suficientes para establecer un procedimiento analítico extenso, que al final, permite llegar a las siguientes expresiones:

𝑇𝑖𝑓𝑙𝑥 es un valor intermedio que sirve para establecer los parámetros 𝐴 y 𝜎. El conjunto de ecuaciones (7) es válido siempre que exista una curva de tendencia de la variación de masa residual, que se ajuste a la ecuación (6). Es decir, con una tendencia como se muestra en la figura 4. Sin embargo, el comportamiento de la degradación térmica se desvía del indicado en la figura 3.
Para que el ajuste sea más aproximado a la tendencia que muestra un termograma experimental, se ha incorporado el término 𝑇𝑓𝑥(𝑇) que es una función dependiente de la temperatura 𝑇. 𝑇𝑓𝑥 es el conjunto de datos donde cada elemento se calcula de la siguiente forma:

En caso de que el argumento dentro del logaritmo sea un valor menor o igual que cero, o que 𝑚′[𝑖]=0, se hace 𝑇𝑓𝑥(𝑖)=𝑇𝑖𝑓𝑙𝑥.
3. MATERIALES Y METODO
Para la identificación del modelo dinámico representado por la ecuación (6), se tomaron los datos de una termogravimetría realizada a muestras de polietileno de baja densidad (LDPE) disponibles en la página web del concurso universitario “Feria de las Ciencias” realizado con el apoyo de la Universidad Nacional Autónoma de México (UNAM) [20]. Los datos corresponden al registro de la degradación térmica de muestras de bolsas plásticas de material biodegradable. Se efectuaron 4 análisis a sendas muestras de 4𝑚𝑔 a las siguientes velocidades de calentamiento: 1,2,5 y 10°𝐶/𝑚𝑖𝑛.
El procedimiento se realizó utilizando una termobalanza para análisis térmico del departamento de polímeros del Instituto de investigaciones en Materiales de la UNAM. El equipo tenía configurada una interfaz gráfica y la posibilidad de transferir los datos obtenidos como archivo compatible en hoja de cálculo Microsoft Excel®.
El tratamiento de los datos fue realizado mediante el programa Matlab® de Mathworks. Se importaron los datos desde la hoja de cálculo. Una vez disponibles como vectores numéricos, se procedió a generar valores intermedios suavizados mediante interpolación polinómica de Hermite por segmentos [21, Cap. 8] . Cada termograma experimental originalmente contenía entre 25 y 35 datos. Con la interpolación se ampliaron a más de 4000 por cada uno.
A partir de los datos interpolados se dedujo un vector 𝑚′ donde cada elemento era la derivada de la masa respecto a la temperatura, numéricamente evaluada mediante la siguiente expresión:
![]()
Donde 𝑛 es la cantidad de elementos tanto del vector que contiene los valores de temperatura (𝑇), como del que tiene los valores de masa instantánea (𝑚). Siendo 𝑚′el vector con las derivadas puntuales numéricamente halladas mediante (9). Estos valores fueron utilizados para trazar la gráfica 𝑇 𝑣𝑠 𝑚′ que complementó cada termograma.
Los parámetros 𝐴, 𝑇𝑖𝑓𝑙𝑥 y 𝜎, se calcularon tomando 3 pares de puntos (𝑇,𝑚)de cada termograma (uno para cada velocidad de calentamiento) y a partir de la gráfica 𝑇 𝑣𝑠 𝑚′(𝑇). El par (𝑇1,𝑚1) se seleccionó de la región de la gráfica 𝑇 𝑣𝑠 𝑚′ (Figura 4) correspondiente a una temperatura menor a donde se ubica el punto de inflexión. El punto (𝑇2,𝑚2) se tomó correspondiente a la temperatura donde ocurre el punto de inflexión (𝑚′𝑚𝑖𝑛 𝑒𝑛 𝑙𝑎 𝑓𝑖𝑔𝑢𝑟𝑎 4). El par (𝑇3,𝑚3), para una temperatura mayor de donde ocurre el punto de inflexión.
A partir de la expresión (8) se generó el vector de datos 𝑇𝑓𝑥(𝑇) como se indicó previamente. Una vez definidos los parámetros 𝐴,𝑇𝑓𝑥(𝑇),𝜎 en cada termograma, se generó un vector cuyos elementos fueran los valores porcentuales de masa residente instantánea calculados a partir de la ecuación (6), para compararlos con el termograma en particular. Se escribieron funciones “Scripts” en Matlab® que aplicaron las ecuaciones (6)-(9) iterativamente sobre los vectores de datos de temperatura 𝑇 y masa 𝑚.
La ecuación (9) se implementó en el diagrama de bloque denominado “pyrArr” y en el bloque “reac” se discretizó la ecuación (5), basados en los bloques que están disponibles en la librería estándar de Simulink® “User-Defined Functions” (Ver figura 5). El nombre específico del bloque es “MATLAB Function”. Este bloque permite escribir una función de Matlab donde los argumentos de entrada y los valores de salida se corresponden con las señales de entrada y de salida respectivamente en el bloque.
El diagrama de bloques representativo del sistema se muestra a continuación, en la figura 5.
La ecuación (5) se discretizó con el método de Heun y la ecuación (6) con el método de Runge-Kutta de orden 4.
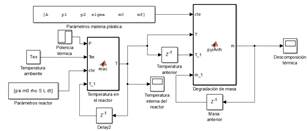
Fig. 5. Diagrama de bloques hecho en Simulink de Matlab para simular la dinámica del proceso de pirólisis de LDPE.
Se realizó una simulación con la herramienta Simulink de Matlab, para combinar las expresiones (5) y (6) en un sistema dinámico. Para validar el modelo se ejecutaron simulaciones en las que la temperatura incrementaba con pendiente constante, con una masa de materia prima inicial, igual a la de las muestras experimentales y una transferencia de calor uniforme, tal como ocurre al interior de una termobalanza para análisis termogravimétrico con velocidad de calentamiento constante. Se utilizaron las mismas velocidades de calentamiento que con las muestras experimentales.
En otra simulación se aplicó una potencia térmica constante. Se utilizaron parámetros 𝜓, 𝜌, 𝑆, 𝐿 teóricos, pues no se cuenta en el momento con un reactor construido, ya que su diseño y montaje es parte de una etapa posterior.
4. RESULTADOS
Los datos experimentales de la degradación térmica del polietileno de baja densidad (LDPE) se muestran en la figura 5, como una serie de 4 termogramas.
La variación del porcentaje de masa respecto a la temperatura, se muestra en la figura 6. Para una mejor visualización, se han mostrado los valores en rangos donde es significativo el cambio. Cada curva corresponde a la degradación del LDPE a diferentes velocidades de calentamiento.
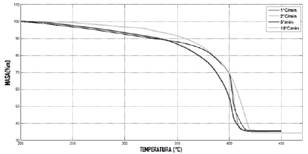
Fig. 6. Gráfica comparativa del proceso experimental de degradación térmica de LPDE a velocidades de calentamiento: 1°𝐶/𝑚𝑖𝑛, 2°𝐶/𝑚𝑖𝑛, 5°𝐶/𝑚𝑖𝑛 y 10°𝐶/𝑚𝑖𝑛.
En la figura 7, se observa la gráfica de 𝑑𝑚𝑑𝑇 vs 𝑇, a partir de la aplicación de la ecuación (9) a los datos interpolados de cada uno de los termogramas experimentales.
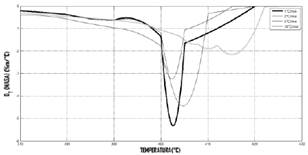
Fig. 7. Gráfica comparativa de la razón de cambio del porcentaje de masa respecto a la temperatura ante diferentes velocidades de calentamiento.
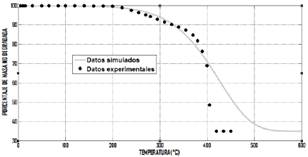
Fig. 8. Comparación entre los datos experimentales del termograma original a una velocidad de calentamiento de 1°𝐶/𝑚𝑖𝑛 con valores arrojados por la simulación basada en la ecuación (6).
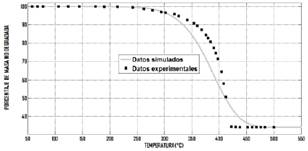
Fig. 9. Datos experimentales del termograma a velocidad de calentamiento de 2°𝐶/𝑚𝑖𝑛 comparados con datos simulados a partir del modelo basado en la ecuación (6).
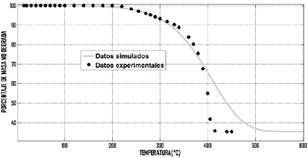
Fig. 10. Datos experimentales del termograma a velocidad de calentamiento de 5°𝐶/𝑚𝑖𝑛 comparados con los datos de la simulación con la ecuación (6).
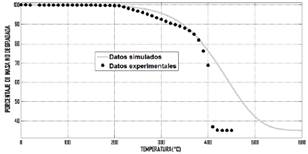
Fig. 11. Datos experimentales del termograma a velocidad de calentamiento de 10°𝐶/𝑚𝑖𝑛 comparados con los datos de la simulación con la ecuación (6).
Las figuras 8, 9, 10 y 11, permiten comparar los resultados simulados con los datos registrados en cada una de las corridas experimentales a las velocidades de calentamiento de: 1,2,5 y 10°𝐶/𝑚𝑖𝑛.
La figura 12 es la respuesta de la temperatura al interior del reactor cuando se aplica una potencia térmica en forma de un paso de 1500𝑊de amplitud. El valor de estado estable de la temperatura es de 929.8°𝐶. En la misma figura, la masa residual se estabiliza en 35.87%
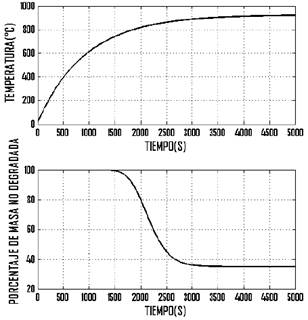
Fig. 12. Comportamiento de la temperatura al interior del reactor y de la degradación de masa según simulación con la aplicación de una potencia térmica de 1500𝑊.
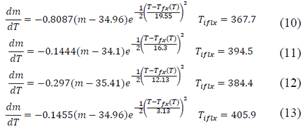
Las ecuaciones (10) a (13) son los casos particulares de la ecuación (6) al sustituir los parámetros 𝐴, 𝜎 y 𝑇𝑖𝑓𝑙𝑥 para cada uno de los termogramas de la degradación térmica a las velocidades de calentamiento: 1,2,5 y 10°𝐶/𝑚𝑖𝑛 respectivamente. Estas 4 ecuaciones fueron las que se utilizaron para generar los puntos de la simulación de cada uno de los termogramas que se pueden comparar en las figuras de la (8) a la (11).
La ecuación (13) es la que se utilizó para simular la respuesta a la entrada de potencia paso. La constante de tiempo 𝜏=890𝑠.
5. DISCUSIÓN
Aunque los resultados simulados se aproximan aceptablemente a los datos experimentales, es necesario realizar análisis matemático en profundidad para formular un criterio que permita seleccionar la mejor triada de puntos del termograma. De hecho, se puede aplicar el procedimiento indicado a triadas diferentes de datos y es muy probable que siempre se obtengan parámetros diferentes en cada caso. Es decir, para cada termograma existe una familia de expresiones que tienen la forma de la ecuación (6) que sin embargo puedan dar origen a simulaciones que se acercarán a la tendencia de los datos experimentales. En este orden de ideas, será necesario realizar trabajo estadístico para formular criterios concretos que permitan escoger los parámetros óptimos que minimicen el error entre datos simulados y valores experimentales.
La función 𝑇𝑓𝑥(𝑇) mostró tener tendencia lineal y mediante la expresión general 𝑇𝑓𝑥(𝑇)=𝑝1𝑇+𝑝2 se logró una mejor aproximación que asumiendo 𝑇𝑓𝑥=𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒. Para reducir el error entre los datos experimentales y los simulados, cuando la masa no degradada está por debajo del 60%, será necesario un análisis del comportamiento de 𝑇𝑓𝑥(𝑇) que es donde se presenta mayor discrepancia.
La geometría del reactor definirá el grosor y área de la cobertura que tendrán que aplicarse a la fórmula (5). Sin embargo, los parámetros 𝜓 y 𝜌 requieren seguir un procedimiento estándar basado en el análisis de la respuesta paso. Tales valores sólo podrán ser numéricamente definidos realizando pruebas con el reactor a escala de laboratorio. Aunque el comportamiento dinámico puede ser descrito con buena aproximación por la ecuación diferencial (5) en cuanto a la temperatura, los valores particulares no pueden estimarse sin primero tener acceso a resultados experimentales con el sistema en operación.
En el rango de temperaturas que va desde el valor en grados centígrados donde ocurre el punto de inflexión, se presenta mayor discrepancia entre los datos experimentales y los datos simulados. Este rango es donde la masa instantánea cae por debajo del 50%.
6. CONCLUSIONES
El procedimiento expuesto en este documento y que toma los datos de un análisis termogravimétrico de LDPE de bolsas biodegradables para determinar los parámetros de la ecuación (6) se aproxima bien al comportamiento real de la degradación térmica. Es razonable asumir que el modelo condensado en la ecuación (6) en combinación con la ecuación (5) es una buena forma de evaluar y proyectar el comportamiento esperado de la degradación térmica de polímeros con comportamiento no segmentado como el LDPE, como parte del proceso de pirólisis de residuos plásticos urbanos. Una vez determinados los parámetros del reactor, el modelo tiene el potencial de convertirse en una herramienta útil para el diseño del sistema de control, así como para la evaluación de estrategias de regulación del proceso.
La mayor divergencia ocurre en la zona de degradación por debajo del 50% y hasta que se estabiliza la cantidad de fracción sólida residual, implica que se tendrán deficiencias para predecir el comportamiento real del proceso en ese rango de temperaturas. Sin embargo, son coincidentes los valores en estado estable y en buena parte del dominio de valores de 𝑻, por lo que es posible superar la deficiencia con la aplicación de un análisis que permita encontrar una relación matemática más ajustada y confiable en ese rango. Es una desventaja menor si se tiene en cuenta que el error de ajuste general es menor al 10%.
La selección de la triada de datos del termograma arroja resultados consistentes si los puntos son tomados a partir de la gráfica 𝑇 𝑣𝑠 𝑚′(𝑇) en la región que se asemeja a la campana gaussiana invertida. Uno de los datos se toma del mínimo local y los otros dos a la izquierda y a la derecha de la temperatura del punto de inflexión. Con este criterio se logró que los valores de los parámetros 𝐴,𝜎 y 𝑇𝑖𝑓𝑙𝑥 tuvieran valores reales a partir de los cuales el procedimiento restante conducía a resultados de simulación satisfactorios. Cuando se intentó con puntos alejados del punto de inflexión o muy adyacentes, ocurrieron indeterminaciones matemáticas debido a que los parámetros provenían de logaritmos de números negativos, cero o raíces cuadradas de números negativos.
La simulación indica que es posible controlar la tasa de degradación de la masa manipulando la potencia térmica aplicada. Esto tiene interesantes implicaciones, entre otras: mantener la temperatura al interior del reactor para lograr uniformidad en la transferencia térmica y de esta forma, garantizar que los gases volátiles y los líquidos combustibles o los materiales químicos sean extraídos sin que se mezclen especies químicas distintas en los flujos de salida. Es importante porque la pureza de las fracciones gaseosa y líquida elimina la necesidad de agregar etapas de separación, reduciendo costos. Otra implicación es la posibilidad de encontrar las temperaturas específicas en las que se producen las diferentes sustancias. Con un control de temperatura y un mecanismo que garantice una transferencia térmica homogénea, se brinda selectividad para configurar el proceso de acuerdo al tipo de producto que se requiera y a las características a pedido de los potenciales clientes.
7. AGRADECIMIENTOS
Los autores agradecen el apoyo recibido de parte de la Escuela de Ciencias Tecnológicas de Facultad de Estudios a Distancia FESAD, a la Facultad de Ciencias, a los grupos de investigación DANUM y TICA, así como al Instituto para la Investigación e Innovación en Ciencia y Tecnología de Materiales INCITEMA. Este artículo es producto del proyecto “Control del proceso de pirólisis de residuos plásticos urbanos no aptos para reciclaje primario” registrado en la Dirección de Investigaciones DIN de la UPTC código SGI:2108.
8. Referencias Bibliográficas
[1] M. Sharon y M. Sharon, Carbon Nano Forms and Applications. McGraw-Hill, 2010.
[2] N. Patni et al., “Alternate Strategies for Conversion of Waste Plastic to Fuels, Alternate Strategies for Conversion of Waste Plastic to Fuels”, Int. Sch. Res. Not. Int. Sch. Res. Not., vol. 2013, 2013, p. e902053, may 2013.
[3] “Plastics—Materials and Processing Technology - Access Engineering from McGraw-Hill”. [En línea]. Disponible en: about:reader?url=http%3A%2F%2Fbiblio.uptc.edu.co%3A2068%2Fbrowse%2Fpolymer-science-and-technology-plastics-rubbers-blends-and-composites-third-edition%2Fc9780070707047ch08%3Fq%3Dexpanded%2Bpolystyrene%23c9780070707047ch08lev1sec06. [Consultado: 24-nov-2015].
[4] J. D. Menczel y R. B. Prime, Thermal Analysis of Polymers: Fundamentals and Applications. John Wiley & Sons, 2014.
[5] X. E. Castells y E. V. García, La pirolisis: Tratamiento y valorizacion energética de residuos. Ediciones Díaz de Santos, 2012.
[6] K. Pielichowski y J. Njuguna, Thermal Degradation of Polymeric Materials. Shrewsbury, GBR: Smithers Rapra, 2005.
[7] H. F. Mark, Encyclopedia of Polymer Science and Technology, Concise. John Wiley & Sons, 2013.
[8] S. D. Anuar Sharuddin, F. Abnisa, W. M. A. Wan Daud, y M. K. Aroua, “Energy recovery from pyrolysis of plastic waste: Study on non-recycled plastics (NRP) data as the real measure of plastic waste”, Energy Convers. Manag., vol. 148, pp. 925–934, sep. 2017.
[9] M. Syamsiro et al., “Fuel Oil Production from Municipal Plastic Wastes in Sequential Pyrolysis and Catalytic Reforming Reactors”, Energy Procedia, vol. 47, pp. 180–188, 2014.
[10] A. Fråne et al., Collection & recycling of plastic waste: Improvements in existing collection and recycling systems in the Nordic countries. Nordic Council of Ministers, 2014.
[11] R. Miandad, M. A. Barakat, A. S. Aburiazaiza, M. Rehan, I. M. I. Ismail, y A. S. Nizami, “Effect of plastic waste types on pyrolysis liquid oil”, Int. Biodeterior. Biodegrad., vol. 119, pp. 239–252, abr. 2017.
[12] N. Miskolczi y R. Nagy, “Hydrocarbons obtained by waste plastic pyrolysis: Comparative analysis of decomposition described by different kinetic models”, Fuel Process. Technol., vol. 104, pp. 96–104, dic. 2012.
[13] J. Bruchmüller, B. G. M. van Wachem, S. Gu, K. H. Luo, y R. C. Brown, “Modeling the thermochemical degradation of biomass inside a fast pyrolysis fluidized bed reactor”, AIChE J., vol. 58, núm. 10, pp. 3030–3042, oct. 2012.
[14] Z. Jin, D. Chen, L. Yin, Y. Hu, H. Zhu, y L. Hong, “Molten waste plastic pyrolysis in a vertical falling film reactor and the influence of temperature on the pyrolysis products”, Chin. J. Chem. Eng., ago. 2017.
[15] C. G. Mothé y I. C. de Miranda, “Study of kinetic parameters of thermal decomposition of bagasse and sugarcane straw using Friedman and Ozawa–Flynn–Wall isoconversional methods”, J. Therm. Anal. Calorim., vol. 113, núm. 2, pp. 497–505, abr. 2013.
[16] C. Trapp, M. Cady, y C. Giunta, Students Solutions Manual to Accompany Physical Chemistry: Quanta, Matter, and Change 2e. OUP Oxford, 2013.
[17] S. Vyazovkin, Isoconversional Kinetics of Thermally Stimulated Processes. Springer, 2015.
[18] D. A. Skoog, S. R. Crouch, y F. J. Holler, Principios de analisis instrumental / Principles of Instrumental Analysis. Cengage Learning Latin America, 2008.
[19] S. G. Ruiz, M. I. S. Alonso, y D. P. Quintanilla, Analisis Instrumental. Netbiblo, 2009.
[20] “Energía de Activación y Velocidad de Degradación de una Bolsa Biodegradable”. [En línea]. Disponible en: http://www.feriadelasciencias.unam.mx/anteriores/feria21/feria194_01_energia_de_activacion_y_velocidad_de_degradacion_d.pdf. [Consultado: 19-may-2016].
[21] G. Farin, Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide. Elsevier, 2014.