1. INTRODUCTION
Unmanned Aerial Vehicles (UAVs) constitute a field that has motivated the control community during the last years. UAVs are used in many applications such as, search, rescue, surveillance, aerial cinemato-graphy, inspection, and mapping. This paper deals with a four-rotor helicopter known as quadrotor, shown in Figure 1. The used quadrotor helicopter has some advantages over conventional helicopters on inspection task. They can take off and land in limited spaces and hover. The control of this machine is a great challenge, therefore, it is suited for the development and testing of new control strategies due to its high nonlinearity of its dynamic model [1]. Moreover, this system is under-actuated because it has six degrees of freedom while it has only four inputs (four rotors). It is not possible to control all of the states at the same time.
On the other side, several controllers have been developed to stabilize the attitude of quadrotors, such as, the feedback linearization method [2] or nonlinear control techniques like backstepping [1], [3],[4],[5] and [6], sliding-mode techniques [1], [3], 𝐻∞controller [7], sliding mode control driven by sliding mode disturbance observer [8], adaptive trajectory track-ing control algorithm [9], controller parameterized [10], super twisting control algorithm for trajectory tracking [11], [12], nonlinear adaptive state feed-back controller [13]. This paper deals with the design of a nonlinear control algorithm for the position and attitude tracking of the quadrotor taking into account nonholonomic constraints. Added to this, it is consi-dered the case in which velocity measurements are not available, then an observer is designed to estimate these variables based in GSTA. The GSTA is able to ensure robustness with respect to bounded external disturbances while reducing the chattering phenomenon caused by all first order sliding mode based controllers. This technique differs from conventional Super-Twisting Algorithm due to the introduction of extras linear terms, that provide more robustness and convergence velocity [14].
The paper is outlined as follows. In section II, the dynamic model of the quadrotor UAV is developed. Based on this nonlinear model, we design in section III, Super-Twisting Algorithm controller. In section IV an observer to estimate the velocities of the quad-rotor is designed. Some simulation results are carried out, allowing the analysis of the stability, robustness of the proposed controller in the presence of perturbations are presented in section V. Finally, section VI is a conclusion. The main contributions of this article are described as follows: Design of an attitude and position controller based on the Generalized Super-Twisting Controller. Design of a state observer based on GSTA for robust velocity estimation. Alternative stability proof for the GSTA.
2. QUADROTOR MODEL
The dynamic model helicopter has been described in several articles as seen in [1], [15] [16], [17], [18] and [19]. The absolute position and the attitude of the quadrotor are described respectively by 𝑋=[𝑥,𝑦,𝑧]𝑇 and the Euler angles 𝛩=[𝜓,𝜃,𝜑]𝑇, corresponding to an aeronaut-tical convention. The equation of the dynamics of rotation of the quadrotor will be:
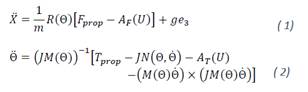
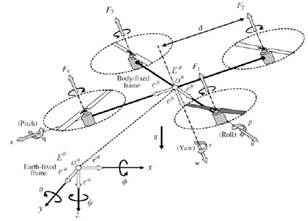
Fig. 1. Quadrotor schematic taken from [11].
Where 𝑀(Ѳ) and 𝑁(Ѳ,Ѳ̇) are given by:
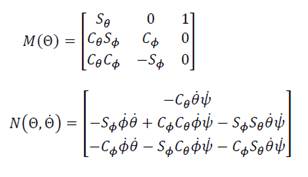
The orthogonal rotation matrix 𝑅(Θ) is defined as follows:
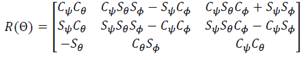
Where cos(∗)=𝐶∗ and sin(∗)=𝑆∗. The inertia matrix of the quadrotor is represented as 𝐽=𝑑𝑖𝑎𝑔[𝐼𝑥,𝐼𝑦,𝐼𝑧]. g is the gravity; the vector 𝑒3 = [0; 0; 1]𝑇; m is the mass of the vehicle; 𝑈 is the velocity of the quadrotor with respect to the air; 𝐴𝐹(𝑈) and 𝐴𝑇(𝑈) are respectively two complex non-linear functions vectors which represent aerody-namic forces and torques in the propeller system. Finally, 𝐹𝑝𝑟𝑜𝑝 and 𝑇𝑝𝑟𝑜𝑝 are the force and torque vectors in the system given by:
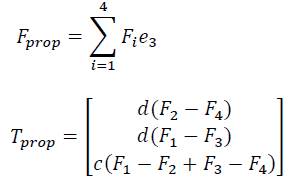
Where 𝑐>0 is the drag factor.
3. CONTROLLER DESIGN
In this section, we design the controllers for the position and attitude of quadrotor using the Super-Twisting Algorithm.
3.1. Attitude controller design
From (2), we define the following state variables:
![]()
Then the state-space form of this model is given by:
![]()
Where 𝑤(𝑡) = [𝑤1; 𝑤2; 𝑤3]𝑇 is the vector of disturbance; 𝑇𝑝𝑟𝑜𝑝 = 𝑢 = [𝑢; 𝑢; 𝑢]𝑇 is the vector of attitude control. The vectors 𝑓(𝑞) and 𝑝(𝑞) are defined as follows:
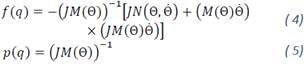
For the design of control, the following assumptions are needed [1]:
Assumption 1. 𝑋,Ѳ,Ѳ̇ can be measured or estimated by on-board sensors.
Assumption 2. The quantity Σ4𝑖=1 represents the total thrust on the body in the z axis and is strictly positive to overcome the gravity.
Assumption 3. The pitch, roll and yaw angles are limited to –𝜋/2<𝜃<𝜋/2 and –𝜋/2<𝜙<𝜋/2 and −𝜋<𝜓<𝜋.
Assumption 4. The desired trajectories and their first and second time derivatives are bounded. Assumption 5. The velocity 𝑈 and 𝑈̇ the acceleration of the quadrotor with respect to the air are bounded.
According to these assumptions, the matrix (5) is non-singular and the following inequalities are satisfied:
![]()
The controller is designed to enforce sliding mode [11] on the manifold:
![]()
Where 𝑒=𝑞𝑑1−𝑞1, 𝑒̇=𝑞̇1𝑑−𝑞2 with 𝑞1𝑑(𝑡)=[𝜑𝑑(𝑡), 𝜃𝑑(𝑡), 𝜓𝑑(𝑡)]𝑇 and 𝛤∈ℝ3×3 is a diagonal positive definite matrix
The proposed control law is in the form:
![]()
Where 𝑣 is the Super-Twisting sliding-mode control given by:

with:
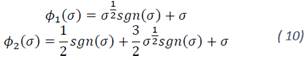
Where 𝑠𝑔𝑛(⋅) denotes the sign function and is defined as:
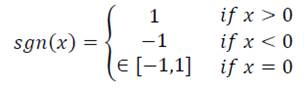
𝐾1=𝑑𝑖𝑎𝑔 [𝑘11, 𝑘12,𝑘13] and 𝐾2=𝑑𝑖𝑎𝑔[𝑘21,𝑘22,𝑘23] are the gain positive definite matrices.
3.2. Position controller design
From (1), we have the following state variables:
![]()
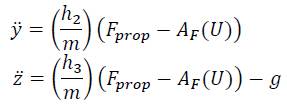
Where:
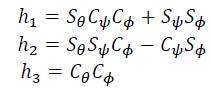
Let the state variables defined by:
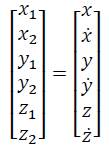
Now, the system (11) is given in the next form:
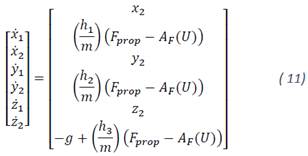
Following the methodology of the previous section, the controller is designed to enforce sliding mode on the manifold:
![]()
Where the position error and its derivative are defined respectively as 𝑟=[𝑥1𝑑−𝑥1,𝑦1𝑑−𝑦1,𝑧1𝑑−𝑧1]𝑇 and 𝑟=[𝑥̇1𝑑−𝑥2,𝑦̇1𝑑−𝑦2,𝑧̇1𝑑−𝑧2]𝑇 with Δ∈ℝ3×3 is a diagonal positive definite matrix. 𝐴𝐹(𝑈) is considered as a bounded perturbation.
The Super-Twisting controller:
![]()
With 𝑖=1,2,3. Where:
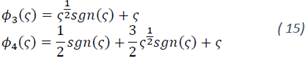
The gain matrices 𝐾3=𝑑𝑖𝑎𝑔[𝑘31,𝑘32,𝑘33], 𝐾4=𝑑𝑖𝑎𝑔[𝑘41,𝑘42,𝑘43] are positive definite.
From (12) the controller for 𝑧 is obtained as:
![]()
Note from (12) that is only possible to control the attitude of quadrotor directly due to the form of 𝐹𝑝𝑟𝑜𝑝, while the (𝑥−𝑦) control is done by modifying the Euler angles (𝜙−𝜃). Therefore, a first step in controlling the position of the quadrotor on the (𝑥−𝑦)axes, a virtual controller is proposed as follows:
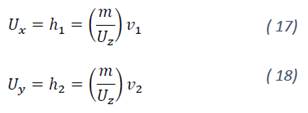
From the equations above, 𝑈𝑧 only tends to zero when the helicopter is on the ground, therefore, the expression (17)-(18) is not indeterminate.
The next step is to find algebraic relations between virtual controllers and the Euler angles desired. From (11) without considering the effect of the given disturbance and maintaining the variable 𝜓𝑑 free, we obtained the following expressions:
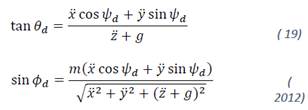
4. OBSERVER DESIGN
In this section, the design of a state observer for estimating speed variables is shown. The high-order sliding mode observer to estimate the altitude velocity has already been implemented [20]. We propose a scenario where only the position variables (𝑥,𝑦,𝑧) are measured and their speed variables are not available, under this assumption is possible to recover exactly and in time finite with only the position measurement using the Generalized Super-Twisting observer [14]:
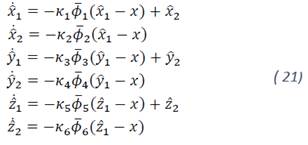
Where 𝜅𝑖 with 𝑖=1,6̅̅̅̅ are the gains of the algorithm and
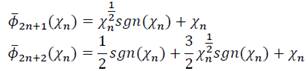
With 𝑛=0,1,2 and 𝜒=[𝜒0,𝜒1,𝜒2]=[𝑥̂−𝑥,𝑦̂−𝑦,𝑧̂−𝑧] and (𝑥̂,𝑦̂,𝑧̂) are the estimated variables. Note that the use of discontinuous injection in 𝜙̅
allows obtaining an exact estimate as discussed below.
5. SIMULATION RESULTS
In this section, we test the robustness of the proposed controller. The quadrotor model parameters used are: 𝑚=0.468𝑘𝑔, 𝐼𝑥=𝐼𝑦=3.83×10−3𝑘𝑔⋅𝑚2, 𝐼𝑧=7.13×10−3𝑘𝑔⋅𝑚2 and 𝑔=9.81 𝑚/.
The controller parameters for the attitude control were selected as: Γ=diag[2,2,2], K1=4√W, K2=2W, where W=diag[12,12,8]. For the position controller: Δ=Γ, K3=8√W, K4=4W.
For the observer, selected gains were as follows: 𝜅1=𝜅3=𝜅5=10 and 𝜅2=𝜅4=𝜅6=2𝜅1.
The proposed trajectory is a spiral whose three-dimensional parametric expression is given by the function:
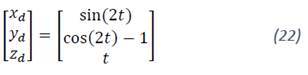
The external disturbance in (1) is defined by
![]()
Where:
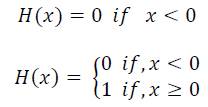
This external disturbance lasted two seconds in the span of 2 to 3 seconds as shown in Figure 2. A low pass filter with transfer function, 𝐿𝑃𝐹=10/(𝑠+10) (𝑠 is the Laplace variable) is applied to 𝜓𝑑 and 𝜃𝑑 in order to minimize the chattering effect in the references. The results show that the vehicle follows the desired path even in the presence of the large external perturbation.
The controller performance for the position and orientation of the quadrotor respectively are shown in figures 2 and 3.
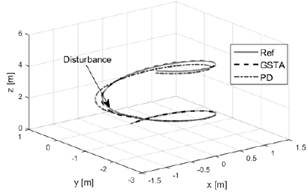
Fig. 2. Path tracking of the quadrotor.
Figures 3 and 4 show the orientation and the desired orientation of the quadrotor during the test maintaining 𝜓𝑑=0.
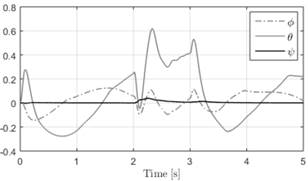
Fig. 3. Euler angles 𝜙, 𝜃 and 𝜓 in tracking disturbance test.
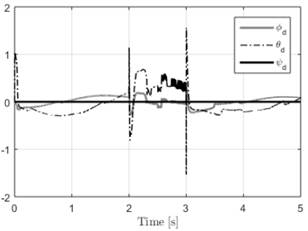
Fig. 4. Desired Euler angles 𝜙𝑑 , 𝜃𝑑, 𝜓𝑑 in tracking disturbance test.
Figures 5 and 6. Also, the effect of the external disturbances is shown. From these figures we can see that the control signals have low amplitude chattering.
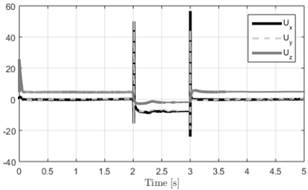
Fig. 5. Controller outputs in tracking disturbance test.
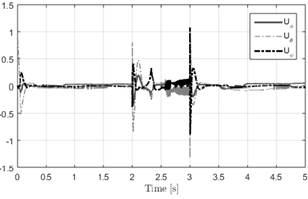
Fig. 6. Controller outputs in tracking disturbance test.
The Figure 7 shown the tracking error of the position controller. Also, these plots demonstrate that the position and the attitude of quadrotor are clearly affected by the external disturbance but the controller estimate the disturbance and compensate for it quickly such that the errors converge to zero.
Finally, Figure 8 shows the velocity estimation. From this plot we can see that the estimated velocities converge to the actual values despite the disturbance introduced in the test.
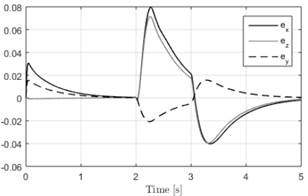
Fig. 7. Error tracking in disturbance test.
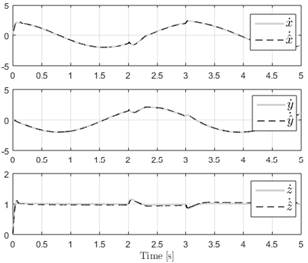
Fig. 8. Velocity variables (gray) and estimated velocity variables (dotted line) under perturbation test (2-3 seconds).
We show that the performance of the GSTA controller presents better results compared to a classic controller such as the PD controller (figure 9). To evaluate the performance of the controllers we use the average Euclidean distance, given by the following equation.
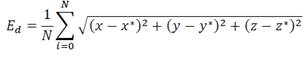
Where 𝑥𝑑, 𝑦𝑑 and 𝑧𝑑 are the desired path, 𝑥∗, 𝑦∗ and 𝑧∗ are the trajectories obtained with the controllers. N is the number of samples.
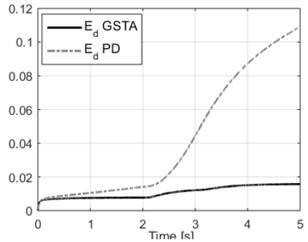
Fig. 9. Performance of the proposed controller and PD.
6. CONCLUSIONS
In this paper, a super twisting controller algorithm to solve the path tracking problem for a quadrotor has been presented. The controller has been designed using second order sliding mode approach in order to reduce chattering phenomenon and to ensure robustness with respect to external disturbances. The whole system was divided into six subsystems. Three of them represent the attitude of quadrotor and have implemented the super-twisting algorithm to stabilize the roll, pitch and yaw angles. The rest subsystems have implemented the super twisting algorithm too, in order to tracking control of quadrotor and taking into account nonholonomic constraints, it was possible modified the yaw and roll angles necessary for displacement on x and y axes. Also, it is assumed that the velocities are not available and were estimated by the Generalized Super-Twisting observer. The simulation results obtained on a quadrotor system show the effectiveness of the proposed controller in the stabilization, path tracking and disturbance rejection cases.
APPENDIX 1: LYAPUNOV STABILITY OF THE SUPER-TWISTING ALGORITHM
Based in [11]. From (6) and (11), the closed loop dynamics is given by:
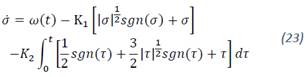
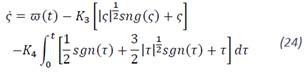
Let:
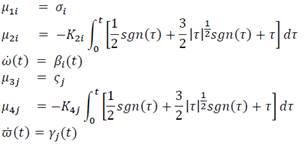
Then (23) and (24) can be rewritten in scalar form (𝑖,𝑗=1,3̅̅̅̅) as:
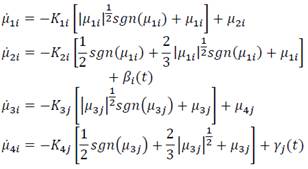
Without loss of generality, we can choose a single component of the system above and simplifying the notation as follows:
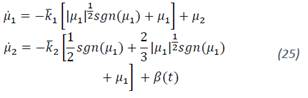
The Lyapunov candidate function is given by
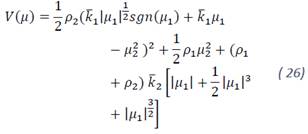
Note that the proposed Lyapunov candidate function is a continuous, positive definite and differentiable function except in 𝜇1=0. This function can be rewritten in quadratic form 𝑉(𝜇)=𝜉𝑇𝑃𝜉 where 𝜉𝑇=[|𝜇1|1/2 𝑠𝑔𝑛(𝜇1),𝜇1,𝜇2] , then:
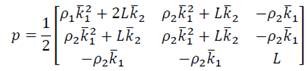
where 𝐿= 𝜌1+𝜌2. If the scalar free parameters 𝜌1, 𝜌2,𝑘̅1 and 𝑘̅2 are chosen positive, then 𝑉(μ) is a positive definite matrix.
Now, this form satisfies:
![]()
Where ‖𝜉‖22=|𝜇1|+𝜇21+𝜇22 is the Euclidean norm of ξ. The time derivative along the trajectories of the system is:
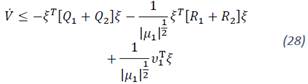
Where:

Suppose that the perturbation terms of (25) are globally bounded by Assumption 5. Then, the time derivative of the Lyapunov function can be rewritten as follows:
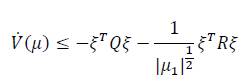
Where 𝑄=𝑄1+𝑄2 and 𝑅 = 𝑅1+𝑅2-𝛿𝑅3. The matrix 𝑅3 is given by:
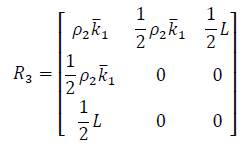
Choosing the parameters 𝜌1>0, 𝜌2>0 the gains 𝑘̅1>0, 𝑘̅2>𝛿 and also high enough, matrices 𝑄 and 𝑅 are positive definite. Under the conditions described:
![]()
Using (27), (29) and also:
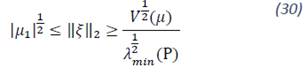
It follows that:
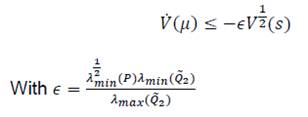
Solving its analog differential equation:
![]()
The solution is given by:
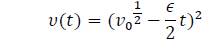
And using the comparison principle, the solution converges in finite time to the origin with 𝑇=2𝑉1/2(𝜇0)\𝜖 units of time.
Finally, 𝜇1=0 in finite time and according to (6) and (13) this implies that lim𝑡→∞𝑒=0 and lim𝑡→∞𝑒̇=0 and lim𝑡→∞𝑟=0 and lim𝑡→∞𝑟̇=0
7. ReferencEs
[1] Madani, T. and Benallegue, A. Backstepping sliding mode control applied to a miniature quadrotor flying robot, in IEEE Industrial Electronics, IECON 2006-32nd Annual Conference on, pp. 700–705, IEEE, 2006.
[2] Lee, S.-h., Kang, S. H., and Kim, Y., Trajectory tracking control of quadrotor uav, in Control, Automation and Systems (ICCAS), 2011 11th International Conference on, pp. 281–285, IEEE, 2011.
[3] Bouabdallah, S. and Siegwart, R. Backstepping and sliding-mode techniques applied to an indoor micro quadrotor, in Robotics and Automation, 2005. ICRA 2005. Proceedings of the 2005 IEEE International Conference on, pp. 2247–2252, IEEE, 2005.
[4] Zuo, Z. Trajectory tracking control design with command-filtered compensation for a quadrotor, Control Theory & Applications, IET, vol. 4, no. 11, pp. 2343–2355, 2010.
[5] Madani, T. and Benallegue, A. Sliding mode observer and backstepping control for a quadrotor unmanned aerial vehicles, in American Control Conference, 2007. ACC’07, pp. 5887–5892, IEEE, 2007.
[6] Bouadi, H., Bouchoucha, M., and Tadjine, M. Sliding mode control based on backstepping approach for an uav type-quadrotor, World Academy of Science, Engineering and Technology, vol. 26, no. 5, pp. 22– 27, 2007.
[7] Raffo, G. V., Ortega, M. G. and Rubio, F. R. Backstepping/nonlinear h control for path tracking of a quadrotor unmanned aerial vehicle, in American Control Conference, 2008, pp. 3356–3361, IEEE, 2008.
[8] Besnard, L., Shtessel, Y. B., and Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer, Journal of the Franklin Institute, vol. 349, no. 2, pp. 658–684, 2012.
[9] Zuo, Z. Adaptive trajectory tracking control design with command filtered compensation for a quadrotor, Journal of Vibration and Control, vol. 19, no. 1, pp. 94–108, 2013.
[10] Mellinger, D., Michael, N. and Kumar, V., Trajectory generation and control for precise aggressive maneuvers with quadrotors, The International Journal of Robotics Research, p. 0278364911434236, 2012.
[11] Derafa, L., Benallegue, A. and Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors uav, Journal of the Franklin Institute, vol. 349, no. 2, pp. 685–699, 2012.
[12] Luque-Vega, L., Castillo-Toledo, B. and Loukianov, A. G. Robust block second order sliding mode control for a quadrotor, Journal of the Franklin Institute, vol. 349, no. 2, pp. 719–739, 2012.
[13] Cabecinhas, D., Cunha, R. and Silvestre, C. A nonlinear quadrotor trajectory tracking controller with disturbance rejection, Control Engineering Practice, vol. 26, pp. 1–10, 2014.
[14] Moreno, J. A. Lyapunov approach for analysis and design of second order sliding mode algorithms, in Sliding Modes after the first decade of the 21st Century, pp. 113–149, Springer, 2011.
[15] Bošnak, M., Matko, D. and Blažič, S. Quadrocopter control using an on-board video system with off-board processing, Robotics and Autonomous Systems, vol. 60, no. 4, pp. 657–667, 2012.
[16] Cai, G., Chen, B. M., Peng, K., Dong, M. and Lee, T. H. Modeling and control of the yaw channel of a uav helicopter, Industrial Electronics, IEEE Transactions on, vol. 55, no. 9, pp. 3426–3434, 2008.
[17] Bouabdallah, S. and Siegwart, R. Full control of a quadrotor, in Intelligent robots and systems, 2007. IROS 2007. IEEE/RSJ international conference on, pp. 153–158, IEEE, 2007.
[18] Moreno, J. A. and Osorio, M. A. Lyapunov approach to second-order sliding mode controllers and observers, in Decision and Control, 2008. CDC 2008. 47th IEEE conference on, pp. 2856–2861, IEEE, 2008.
[19] Xiong, J. J., and Zhang, G. B. Global fast dynamic terminal sliding mode control for a quadrotor UAV. ISA transactions, 66, 233-240, 2017.
[20] Gonzalez-Hernandez, I., Palacios, F. M., Cruz, S. S., Quesada, E. S. E., and Leal, R. L. Real-time altitude control for a quadrotor helicopter using a super-twisting controller based on high-order sliding mode observer. International Journal of Advanced Robotic Systems, 14(1), 2017.