1. INTRODUCCIÓN
La navegación autónoma de robots móviles ha tomado protagonismo en el desarrollo tecnológico de las últimas décadas, desde asistentes personales, robots de limpieza, transporte de carga en interiores y exteriores, especialmente para organizar bodegas o en la entrega de productos como repartir pizzas, e incluso, este campo de la robótica ha incursionado en la exploración espacial [1].
Con el fin de desarrollar estrategias para la navegación de robots móviles, en [2] Siegwart et al. hace referencia a procesos tales como: la planificación que hace referencia al conocimiento previo que posee la máquina del ambiente que va a navegar, y puede ser usado para generar rutas que lleguen a una meta en particular; el otro proceso es el reconocimiento del entorno, en el que se habla de la información que provee los sensores sobre el ambiente, y la interacción de los actuadores del robot frente a posibles obstáculos que pueda encontrar.
Hablando más a fondo sobre la etapa de reconocimiento del entorno, en [3] y [4], se sugiere que los errores propios de un sistema como el robot móvil, tales como: la lectura de los sensores, la acción de los actuadores o el procesamiento mismo de los datos puede acarrear incoherencias en la información para planear movimientos futuros del robot, afectan el normal funcionamiento de este; y a esto, hay que tener en cuenta que las acciones propias del robot, altera directamente el entorno en el que se está moviendo, por lo que esto puede generar aún más errores en el proceso.
Con el fin de lidiar con los errores propios de la robótica móvil, se han desarrollado diferentes técnicas de filtrados, entre las que se destacará en este trabajo el filtrado bayesiano, que se basa en predecir información a partir de los estados pasados del robot y corrigiendo estos resultados con la información que proviene de los sensores [5].
Entre los filtros bayesianos más usados, se encuentra el filtro de Kalman, propuesto por Kalman et al. en [6] y [7], en donde se da una solución óptima al problema del filtrado a partir de suposiciones tales como: el sistema es lineal, y la dinámica del sistema estudiado sigue un proceso gaussiano.
El filtro de Kalman posee diferentes variaciones, como el filtro de Kalman extendido o el unscented Kalman filter, que pueden ser usados en sistemas no lineales, como lo sugiere Simon en [8]. Pero, en el caso de que el sistema no posea un comportamiento gaussiano o de no linealidades fuertes, se entra en el campo de filtros no paramétricos, donde se encuentra el filtro de partículas desarrollado por N. Gordon en [9], enfocado en un primer momento a la visión artificial, pero diversificado a otros campos, como la robótica, la econometría, ingeniería química, entre otros [10] [11].
Estos filtros bayesianos han sido usados en los últimos años como estimadores de estado en robótica móvil, buscando obtener una mejor estimación en la posición del robot. Como por ejemplo el trabajo desarrollado con sistemas multiagente por Luque en [12] o estrategias de navegación con poco conocimiento del entorno como en [13].
Este artículo muestra el uso de filtros bayesianos en combinación con el algoritmo A* para la estimación de la posición de un robot móvil. En la sección 2 se describen los métodos a utilizar, en la sección 3 se muestran los resultados obtenidos en simulación y se discute sobre los mismo, y finalmente la sección 4 tiene las conclusiones.
2. MATERIALES Y METODO
2.1. Filtros bayesianos
Esta sección tratará temas relacionados con los filtros bayesianos implementados en la estimación de estados en robots móviles, así como también, se describirá el caso particular del filtro de partículas como una solución recursiva para este problema.
2.1.1. Estimación de estados mediante filtros bayesianos: Los filtros bayesianos, métodos basados en la predicción y corrección de estados, han sido protagonistas del desarrollo tecnológico de los últimos años, permitiendo analizar con detalle sistemas que poseen un comportamiento con mucho ruido, como es propuesto en Simon en [8].
Así pues, la formulación de los filtros bayesianos parte de un sistema descrito por el estado 𝑣𝑡, cuya medición, en el tiempo 𝑡, está dada por 𝑤𝑡, y una entrada 𝑢𝑡. Considerando la ecuación (1), que hace referencia a la función de creencia del sistema y que representa la relación condicional del estado, respecto a las entrada y mediciones, desde el inicio de las observaciones hasta el tiempo actual [14] y [15].
![]()
Usando el teorema de Bayes en la ecuación (1), esta puede ser reescrita como se muestra en la ecuación (2).
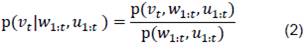
Aplicando teoremas de probabilidad conjunta y probabilidad condicional, se puede reescribir la ecuación (2) como la ecuación (3).
![]()
Si se asume que el sistema posee suficiente información como para analizar el estado actual 𝑣𝑡, entonces es suficiente para predecir la medición 𝑤𝑡; dicho esto, las entradas del sistema anteriores (𝑢1:𝑡−1) son independientes a la medición de los sensores en el estado actual. Así pues, la ecuación (3), se reescribe como la ecuación (4).
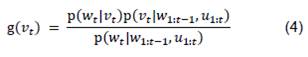
Ahora, sea la ecuación (5) la función de probabilidad a priori del sistema.
![]()
La ecuación (4), es reescrita como la ecuación(6) siendo 𝜂, un factor normalizador, tal que esta ecuación cumpla con la condición expresada en la ecuación (7), para que g(𝑣𝑡) pueda ser considerada función de densidad de probabilidad, que a su vez hace referencia a la función p(𝑤𝑡|𝑤1:𝑡−1,𝑢1:𝑡) de la ecuación (4).
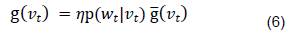
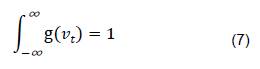
En el anterior análisis se puede observar la recursividad de la formulación bayesiana propuesta para describir el comportamiento del sistema, por medio de la función a priori g̅(𝑣𝑡), la cual depende de las mediciones 𝑤1:𝑡−1 y las entradas 𝑢1:𝑡 del sistema; por otra parte la ecuación (6), también es llamada función de probabilidad a posteriori, dado que depende de las mediciones 𝑤𝑡 y el estado 𝑣𝑡 del sistema.
Así, la función de probabilidad a priori hace referencia a una etapa de predicción de estados, y la función de probabilidad a posteriori, a la etapa de corrección, para dar una estimación del estado del sistema en el tiempo 𝑡. En la Fig. 1, se propone el sistema de un cuerpo moviéndose en línea recta en una dimensión, mostrando así gráficamente, las probabilidades involucradas para estimar los estados de este movimiento.
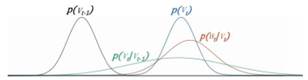
Fig. 1. Probabilidades involucradas en un movimiento rectilíneo de un cuerpo, imagen adaptada de [16].
2.1.2. Filtro de partículas: el filtro de partículas es un filtro bayesiano basado en la metodología Monte Carlo, y parte del supuesto de que el proceso es una cadena de Markov; en este filtro se propone generar 𝑴 muestras aleatorias del estado actual a partir de la función de probabilidad a priori, llamadas partículas, que representan espacios de estado artificiales del sistema; estas partículas son agrupadas en conjuntos que se irán actualizando conforme los sensores tomen medidas y el algoritmo estime posibles nuevos estados del sistema.
Acorde con Thrun en [17], el algoritmo del filtro de partículas, se rige bajo la ley de los grandes números, la cual consiste en que a mayor número de muestras (idealmente, 𝑀→∞), la operación convergerá a una solución al filtrado más fiable. Hay que tener en cuenta que este algoritmo cobra sentido bajo tres suposiciones:
· La función g(𝑣1) está disponible para ser muestreada.
· La forma de la función p(𝑤𝑡|𝑣𝑡) debe ser conocida y no es necesariamente Gaussiana.
· La función de ruido σ en el estado debe estar disponible para tomar muestras.
Así pues, como es propuesto por [9], el filtro de partículas parte de un conjunto de muestras aleatorias 𝑉𝑡−1 = {𝑣{𝑡−1}(𝑖): 𝑖 = 1,2,…,𝑀} tomado de la función de probabilidad p(𝑣𝑡−1|𝑤𝑡−1). A continuación se muestran las etapas de los filtros bayesianos en el filtro de partículas:
· Etapa de predicción: Este conjunto de muestras 𝑉𝑡−1 es evaluada en el modelo del sistema, tal que 𝑉𝑡∗=f(𝑣𝑡(𝑖),𝛿𝑡−1(𝑖)) con el fin de tener muestras a priori en el tiempo 𝑡.
· Etapa de actualización: Después de tomar las medidas 𝑤𝑡, se obtienen los pesos de cada estado 𝑄𝑡={𝑞1,𝑞2,…,𝑞𝑀}, a partir de la ecuación (8).
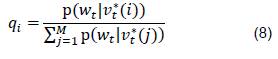
Al llegar a la etapa de actualización, se obtiene una nueva función de probabilidad a priori basada en los pesos de importancia 𝑞𝑖, la cual es remuestrada para obtener un nuevo conjunto de datos 𝑉𝐾={𝑣𝑘(𝑖):𝑖=1,2,…,𝑀} que está distribuido aproximadamente como p(𝑣𝑘|𝑤𝑘).
2.2. Navegación autónoma de robots móviles con locomoción diferenciales
En esta sección se abordarán conceptos relacionados con la estrategia de navegación autónoma desarrollada para implementar el filtro de partículas en un robot móvil de locomoción diferencial, teniendo en cuenta los aspectos previamente mencionados de planificación y reconocimiento del ambiente, y partiendo del supuesto, del conocimiento previo del mapa donde va a moverse el robot.
2.2.1. Modelo cinemático para robots móviles: Acorde con el planteamiento de Siegwart et al. [2], el movimiento de un robot móvil, se describe usando dos sistemas de referencia, un sistema coordenado inercial (𝐈) y móvil (𝐑), mostrados en la Fig. 2.
Para modelar la cinemática de un robot diferencial, se propone la matriz de posición inercial 𝜁𝐼 definida en la ecuación (9).
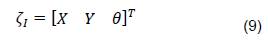
En donde estas variables representan las coordenadas del robot respecto al sistema inercial, siendo 𝜃 el ángulo del robot respecto a la abscisa, 𝑋 es la posición del robot en la abscisa y 𝑌 es la posición del robot en la ordenada.
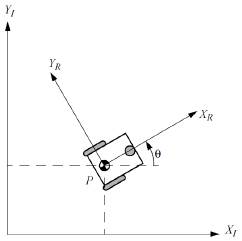
Fig. 2. Sistema de referencia en un robot móvil: inercial (𝐼) y móvil (𝑅), imagen adaptada de [2].
Si se considera que el movimiento del robot, en un principio, puede ser descrito a partir de sus velocidades: de traslación (𝜆) y rotación (𝜔). Con esto, si se toma un intervalo de tiempo muy pequeño, se puede considerar que el movimiento del robot describe un arco de circunferencia, como se muestra en la Fig. 3.
A continuación, se hará el modelamiento presentado por Baturone en [19], en donde la velocidad lineal puede ser descrita por la ecuación (10) mediante la porción de arco recorrida 𝑠; por su parte, la velocidad rotacional se refiere al cambio del ángulo del robot respecto al eje de abscisa del sistema de referencia inercial, véase la ecuación (11).


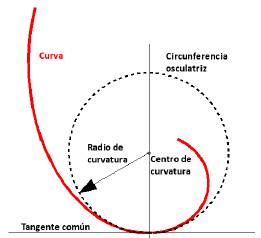
Fig. 3. Circunferencia osculatriz, imagen adaptada de [18].
Por otra parte, la porción de arco, puede ser descrita por la ecuación (12), en donde 𝑟 es el radio de la circunferencia osculatriz.

A partir de estos planteamientos, y tomando en cuenta la Fig. 2, se puede especificar la ubicación del robot respecto al sistema de referencia inercial, tal como se muestran en la ecuación (13).
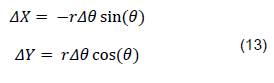
Si se reemplaza la ecuación (12) en la ecuación (13), se tiene (14).
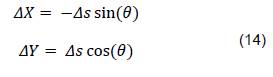
Si la ecuación (14) es dividida a ambos lados por 𝛥𝑡, se obtienen la ecuación (15).
![]()
![]()
Luego, la velocidad angular del robot se observa en la ecuación (16).
![]()
Pasando este modelo a su forma matricial y tomando como referencia la ecuación (9), se tiene la ecuación (17).
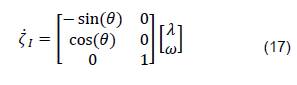
Es importante considerar que este modelo, tal cual como está expresado, no posee variables que se puedan controlar dentro del robot; por lo que se propone considerar este mismo modelo de circunferencia osculatriz para cada llanta del robot diferencial, así las velocidades estarían descritas en las ecuaciones (18), (19); siendo 𝜆𝐼, la velocidad de traslación en la rueda izquierda, análogamente 𝜆𝑑 con la rueda derecha, 𝑅 el radio de las llantas del robot e 𝐼 la separación de estas.
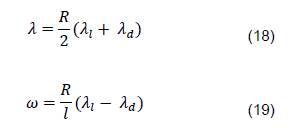
Así pues, despejando las velocidades de cada llanta de (18), (19), se propone entonces las ecuaciones que describen el sistema a controlar, descritas en (20).
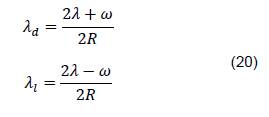
Por último, hay que considerar que la medición de la distancia recorrida, es un proceso acumulativo, por tanto, el modelo de distancia para un robot diferencial es:
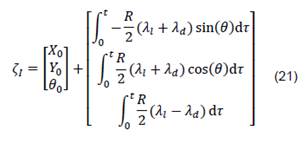
2.2.2. Generación de rutas mediante algoritmo A*: Obtenido el modelo cinemático del sistema, se procede a desarrollar un programa generador de rutas basado en el algoritmo A* planteado por Thrun et al. en [14]. En donde, para este trabajo, parte del supuesto de que el entorno de navegación ya ha sido previamente mapeado, por lo que se conoce la ubicación de los obstáculos, la meta y la posición inicial del robot. En la Fig. 4, se muestra un mapa que utilizado para generar rutas.
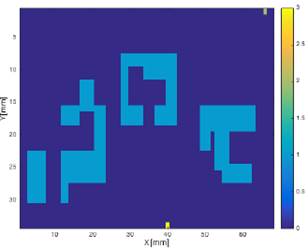
Fig. 4. Representación discreta de un mapa.
Las convenciones de la Fig. 4 se encuentran en la Tabla 1.
Tabla 1. Convenciones para Fig. 4 - Fig. 9.
|
Color |
Descripción |
|
Azul oscuro |
Espacio libre |
|
Azul claro |
Obstáculo |
|
Verde |
Robot |
|
Amarillo |
Meta |
El Algoritmo A* trabaja con dos mapas alternativos para generar las rutas: mapa de costo y mapa de función heurística. Para este trabajo, estas funciones se basan en el planteamiento de [1] y [20] sobre los campos potenciales en la planeación de caminos.
El mapa de costo, consiste en evaluar la distancia existente entre los obstáculos de la pista y cada punto libre en el mapa. Así pues, se hace una analogía en donde los obstáculos repelen al robot, generando posibles rutas que lo alejen de ellos; siguiendo así la ecuación (22), en donde (𝑋,𝑌)𝑜 representan las coordenadas del punto en el contorno del obstáculo más cercano al punto (𝑋,𝑌)𝑙. En la Fig. 5, se encuentra la representación de estos mapas de costos.
![]()
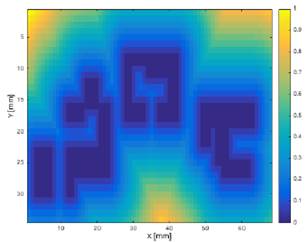
Fig. 5. Mapa de costo para el mapa de la Fig. 4.
Por su parte, el mapa heurístico describe la distancia entre cada punto del mapa y la meta; para este caso, se haría la analogía de que la meta atrae el robot; la ecuación (23) muestra el cálculo para obtener este mapa, siendo (𝑋,𝑌)𝑚 las coordenadas de la meta en el mapa. En la Fig. 6, se muestra el mapa heurístico para el mapa de la Fig. 4.
![]()
Así pues, sumando el mapa de costos y heurístico, se calculó un tercer mapa que sería usado por el algoritmo de búsqueda para encontrar una ruta entre la posición inicial del robot y la meta. En la Fig. 7, se muestra el mapa solución para el caso analizado.
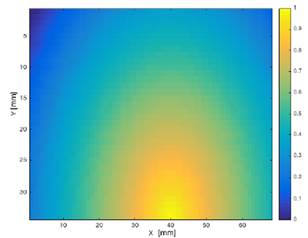
Fig. 6. Representación de mapa heurístico Fig. 4.
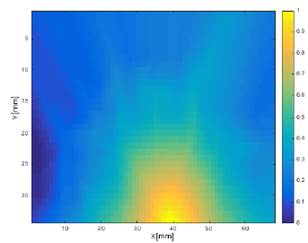
Fig. 7. Mapa de solución para el mapa de la Fig. 4.
Es a aclarar que, tanto en Fig. 5, Fig. 6 y Fig. 7, se hace alusión a que el color amarillo atrae el robot, mientras que el azul lo intenta repeler; así pues, el algoritmo de A*, buscará un camino a partir de las celdas con mayor valor en su función de costo y heurística.
Otro aspecto a analizar es el recorrido de los nodos a partir del mapa de solución obtenido previamente. La Fig. 8, muestra las tres primeras iteraciones para un mapa arbitrario, en donde el robot parte de una posición inicial, el cual es el nodo raíz. La acción de escoger estos nodos en cada iteración se basa en maximizar las funciones heurística y de costos, por tanto, de entre los nodos hijos, se toma aquel que posea un mayor valor en estas funciones.
Los nodos hijos se generan a partir de posibles movimientos que puede hacer el robot en el mapa: ir arriba, abajo, a la derecha, a la izquierda, moverse en diagonal (derecha-arriba, derecha-abajo, izquierda-arriba, izquierda-abajo). Con el fin de alivianar peso computacional, los movimientos ilógicos, es decir, aquellos movimientos en donde el robot se sale del mapa o choca con un obstáculo, no son tenidos en cuenta a priori por el algoritmo de búsqueda.
Cabe mencionar que los caminos generados por este algoritmo, se realizan fuera de línea, dado que esta búsqueda A* consume muchos recursos de la computadora. En la Fig. 9 se muestran la ruta encontrada por el algoritmo para el mapa propuesto.
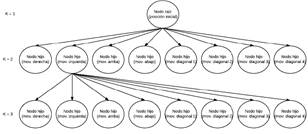
Fig. 8. Representación nodos para búsqueda A*.
Estas rutas generadas serán usadas como referencia para el controlador propuesto. Cabe resaltar también que estas rutas solo proveen un punto de posición (𝑋,𝑌) en el plano cartesiano, dejando a un lado la orientación 𝜃 del robot como variable de control.
2.2.3. Control de posición por persecución pura: En este apartado, se planteará un control por persecución pura propuesto por A. Baturone en [19], cuya variable de control es la velocidad angular del robot 𝜽=𝝎̇, y de esta, dependen las velocidades cartesianas del mismo 𝑿̇, 𝒀̇, en el sistema de ecuaciones (24), se muestra el modelo propuesto.
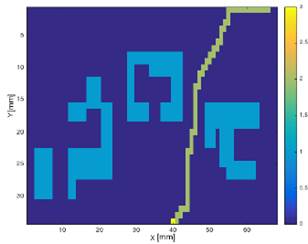
Fig. 9. Mapa con ruta para el mapa Fig. 4.
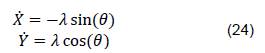
![]()
En donde 𝜆 es una velocidad lineal de referencia, 𝐾𝑝 es la constante proporcional de control (la cual fue seleccionada heurísticamente para este trabajo), y 𝛾 se puede calcular como se muestra en la ecuación (25).
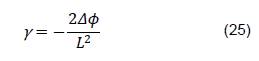
En donde las variables 𝛥𝜙 y 𝐿 son descritas en las ecuaciones (26) y (27).
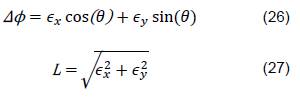
Los errores 𝜖 están dados por el sistema de ecuaciones (28), en donde las variables 𝑇 hacen referencia a las posiciones deseadas del punto en el mapa.
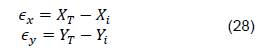
En la Fig. 10, se muestra el diagrama de bloques propuesto para este sistema de control, en donde se tiene en cuenta los ruidos previamente calculados, el modelo directo y el modelo inverso del robot con locomoción diferencial.
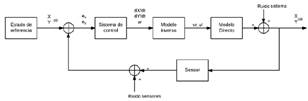
Fig. 10. Diagrama de bloques del sistema.
3. RESULTADOS Y ANÁLISIS
3.1. Simulación del sistema
El entorno de simulación fue desarrollado en la plataforma Matlab®, en el que se simuló el movimiento de robot de locomoción diferencial, haciendo diferentes rutas. A continuación, se mostrarán los resultados obtenidos, dando a conocer en un primer momento el caso del control por persecución pura, en donde se evaluó una trayectoria punto a punto.
En Fig. 11 y Fig. 12, se muestra una simulación punto a punto de control propuesto en esta sección para diferentes valores de 𝐾𝑝, siendo el estado inicial [000]T y el estado objetivo es [2502500]T; con una velocidad lineal de referencia de 100 mm/s.
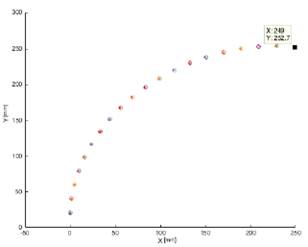
Fig. 11. Seguimiento de trayectoria punto a punto para 𝐾𝑝=1.
Posterior a la verificación de que el controlador estuviera sintonizado con el sistema virtual, se procedió a simular el filtro de partículas, variando el número de partículas en cada caso, con el fin de verificar la ley fuerte de los grandes números en el filtro de partículas.
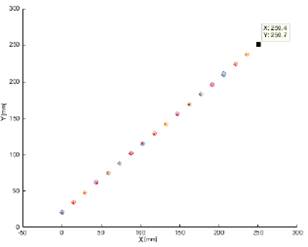
Fig. 12. Seguimiento de trayectoria punto a punto para 𝐾𝑝=10.
Con el fin de simular los sensores, de tal forma que haya una etapa de corrección aportante para el sistema, se usaron los datos del mapa discretizado siguiendo la ecuación (22) para emular tres sensores infrarrojos ubicados a 0º, 45º y -45º respecto a 𝜃. En la Fig. 13, se puede apreciar esta distribución geométrica y la expansión de las partículas conforme avanza el robot en la trayectoria.
La ruta generada a partir del algoritmo A* tiene como obstáculos las paredes que se muestran en gris en la Fig. 13.
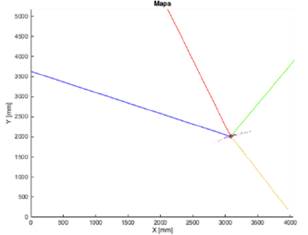
Fig. 13. Sensores en el entorno de simulación
En el caso de la Fig. 14, se muestran gráficamente los resultados para la simulación de 75, 100 y 200 partículas, con el fin de seguir la ruta mostrada en púrpura. Es a destacar que estas estimaciones presentan un sesgo bastante notorio respecto al estado del robot cuando se usan pocas partículas. Nótese que la figura tiene un acercamiento respecto a la Fig. 13
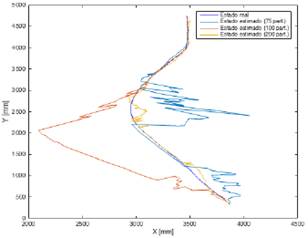
Fig. 14. Simulación del filtro de partículas.
En la Tabla 2, se puede observar los errores promedios del recorrido para las simulaciones, y los tiempos medios de cada iteración de la simulación, teniendo un caso de control en donde hay 0 partículas.
Se puede observar como el error tiende a disminuir conforme las partículas aumenta, mientras que el tiempo promedio por iteración sube considerablemente, dado que el solo hecho de implementar el filtro, implica a priori una carga computacional adicional para la máquina que procesa la información.
Tabla 2. Errores y tiempos promedios de la simulación.
|
Nº de Partículas |
Error [mm] |
Tiempo [s] |
|
0 |
- |
1.6767e-04 |
|
75 |
140.6537 |
0.1497 |
|
100 |
265.8606 |
0.2007 |
|
200 |
39.0811 |
0.2825 |
4. CONCLUSIONES
Con este trabajo, se abordaron diferentes aspectos de la navegación autónoma en robots móviles: simulación de plataformas de locomoción diferencial, control de posición por persecución pura, generación de rutas por medio del algoritmo A* con sus respectivas funciones de costo y heurística, por último, un estimador de estados a través del filtro de partículas, debido a la característica de no linealidad del sistema.
Respecto al controlador propuesto, es una alternativa simple de aplicar, dado que no requiere mucha carga computacional, al ser un control proporcional, pero esto puede generar un esfuerzo de control no deseado en una posible implementación para un sistema físico.
El algoritmo de generación de rutas es una propuesta para trabajo fuera de línea, dado que los cálculos propuestos requieren de una carga computacional considerable, por lo que en trabajos futuros se propone considerar otras formas de discretizar el mapa que alivianen los cálculos del algoritmo, y este pueda ser candidato a implementarse en línea.
Por último, eje central de este trabajo, el filtro de partículas, corroboró que es una alternativa para estimar estados de sistemas no lineales, dado que el seguimiento del estado 𝜁, fue bastante consistente en las simulaciones. Se sugiere desarrollar una metodología experimental de caracterización del filtro, con el fin de tener la cantidad de partícula óptimas para tener una estimación consistente al sistema real, con un bajo coste computacional.
Por lo que se propone para futuros trabajos, implementar filtros más robustos a los sensores, así como también el uso de nuevas propuestas de funciones de probabilidad para el sistema y la paralelización de procesos en este algoritmo, con el fin de disminuir el coste computacional y así, implementarlo en línea. Seguido a esto, se sugiere aprovechar la flexibilidad que supone el filtro de partículas para fusionar sensores tales como una IMU o una cámara, con el fin de obtener una estimación de estados mucho más exacta y poder abordar el problema de la localización global o implementar una localización y mapeo simultaneo (SLAM, por sus siglas en inglés), para explorar entornos desconocidos para el robot, propuesto por Newman en [21] y Durrant-Whyte en [22].
5. AGRADECIMIENTOS
Los autores quisieran agradecer la colaboración de la profesora M.Sc. Mónica Hernández, ya que su experiencia en el campo de estimación de estados usando filtros bayesianos que fue de gran ayuda para la implementación del algoritmo en este proyecto.
6. Referencias Bibliográficas
[1] Dudek, G. y Jenkin, M., Computational principles of mobile robotics. Cambridge University Press, 2010.
[2] Siegwart, R., Nourbakhsh, I. R., y Scaramuzza, D. Introduction to autonomous mobile robots. MIT press, 2011.
[3] García Caicedo, J. M. Navegación de un robot móvil sobre terreno irregular con contacto de su brazo con el suelo [Master Thesis]. Medellín, Colombia: Universidad de Antioquia, 2012.
[4] Rekleitis, I. M. A particle filter tutorial for mobile robot localization. Tech. Rep. TR-CIM- 04-02. Montreal, Canada. Centre for Intelligent Machines, McGill University, 2004.
[5] Chen, Z. Bayesian filtering: From Kalman filters to particle filters, and beyond. Statistics 182 (1), 1-69, 2003.
[6] Kalman, R. E. A new approach to linear filtering and prediction problems. Journal of basic Engineering, 82, 35 - 45, 1960.
[7] Kalman, R. E. y Bucy, R. S.. New results in linear filtering and prediction theory. Journal of basic engineering, 83, 95 - 108, 1961.
[8] Simon, D. Optimal state estimation: Kalman, H infinity, and nonlinear approaches. John Wiley & Sons, 2006.
[9] Gordon, N. J., Salmond, D. J., y Smith, A. F. Novel approach to nonlinear/non-gaussian bayesian state estimation. IEEE Proceedings Radar and Signal Processing, 140, 107–113, 1993.
[10] Doucet, A. y Johansen, A. M. A Tutorial on Particle filtering and smoothing: Fiteen years later. The Oxford handbook of nonlinear filtering, 656–705, 2011.
[11] Arulampalam, M. S., Maskell, S., N. Gordon, y Clapp, T. A tutorial on particle filters for online nonlinear/non-gaussian bayesian tracking. IEEE Transactions Signal Processing, 50, 174 - 188, 2002.
[12] R. R. Luque. Localización multirrobot basada en filtro de partículas [Ph.D. Thesis]. Madrid España: Universidad de Alcalá, 2006.
[13] Cook, G. Mobile robots: navigation, control and remote sensing. John Wiley & Sons, 2011.
[14] S. Thrun, W. Burgard, and D. Fox. Probabilistic robotics. MIT press, 2005.
[15] López, D. G., Aldeguer, R. R., & Ruiz, F. E. Aplicación del muestreo bayesiano en robots móviles: estrategias para localización y estimación de mapas del entorno. Alicante, España: Universidad de Alicante, 1999.
[16] Lee, D. Curso de Coursera: Robotics, Estimation and Learning. Disponible en https://www.coursera.org [consultado el 26 de marzo de 2017].
[17] Thrun, S. Particle Filters in Robotics. Proceedings of Uncertainty in AI, 1, 511 - 518, 2002.
[18] Algarabia. Circunferencia osculatriz. Disponible en https://commons.wikimedia.org/ [consutado el 26 de marzo de 2017].
[19] Baturone, A. O. Robótica: manipuladores y robots móviles. Marcombo, 2005.
[20] Siciliano, B., Sciavicco, L., Villani, L., y Oriolo, G. Robotics: modelling, planning and control. Springer Science & Business Media, 2010.
[21] Dissanayake, M., Newman, P., Clark, S., Durrant-Whyte, H. F., y Csorba, M. A solution to the simultaneous localization and map building (SLAM) problem. IEEE Transactions on Robotics and Automation, 17, 229 - 241, 2001.
[22] Durrant-Whyte, H. y Bailey T. Simultaneous localization and mapping: part I. Robotics & Automation Magazine, 99 - 106, 2006.