1. INTRODUCCIÓN
El robot de dos barras es un manipulador muy conocido en la robótica por su simplicidad mecánica, lo que facilita el análisis cinemático y dinámico, siendo comúnmente utilizado como ejemplo para el análisis de conceptos teóricos [1], [2], [3], [4]. Es su simplicidad que lo ubica como un referente y es utilizado comúnmente para validar o demostrar teorías de control, como puede apreciarse en [5], [6], [7], [8], [9], [10], [11] y [12], entre otros artículos.
La importancia del robot de dos eslabones para la formación académica en el área de robótica es tal, que en la actualidad existe un producto comercial ofrecido por Quanser [13], enfocado en la realización de prácticas de control sobre dicho sistema mecatrónico. Las prácticas de control para este sistema están enfocadas a un control de lazo cerrado tipo proporcional–integral-derivativo, PID, basado en la cinemática inversa del robot.
El presente artículo trata sobre el diseño, construcción y pruebas de un prototipo de robot planar de dos grados de libertad construido para ser utilizado tanto en la enseñanza de la robótica, como en investigación en el área de control de sistemas mecánicos. La parte experimental del artículo se centra en el control articular PID por cuanto es el tipo de control más utilizado en robótica industrial. No se empleó un control no lineal basado en la dinámica del sistema por cuanto este tipo de control requiere de controladores de tiempo real con menor latencia a la que actualmente se tiene.
El principal objetivo del artículo es mostrar la implementación del control cinemático del robot en un ambiente didáctico. Se inicia con el análisis cinemático y la planificación de las tareas. Luego se describe el sistema mecatrónico equivalente al robot de dos eslabones. Se continúa con el sistema de control tipo Proporcional/Derivativo desarrollado en MATLAB/Simulink, para entender el funcionamiento del sistema antes de realizar la experiencia con el sistema físico. Finalmente, se ilustran los resultados obtenidos en los cursos de robótica, complementados con una explicación del error cinemático del equipo.
2. MATERIALES Y METODO
En esta sección se discutirá como controlar el robot para obtener el movimiento deseado del mismo.Para ello se ha dividido en nueve subsecciones. Las tres primeras de ellas explican la cinemática del sistema y los análisis cinemáticos inverso y directo. Las siguientes tres secciones tratan sobre la planificación del movimiento que se requiere para mover el sistema sin aceleraciones bruscas. Las últimas tres secciones explican cómo realizar los movimientos lineales y circulares.
2.1 Análisis Cinemático del Robot
La Fig. 1 ilustra el robot de dos grados de libertad empleado para el análisis. En la base existe el sistema de referencia {0}:{X0,Y0} el cual está unido al cuerpo fijo y sobre el cual se realiza el análisis cinemático de posición. Al final del primer eslabón se encuentra el sistema de dicho cuerpo, con referencia {A}:{XA,YA}. Por último, el sistema de referencia ubicado al extremo del segundo eslabón y con referencia {B}:{XB,YB}.
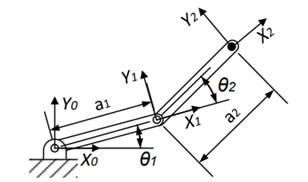
Fig.1. Sistemas de referencia del robot serial 2R
La matriz de transformación homogénea entre el último sistema de referencia, {B} y el sistema base {0} se calcula a través de la expresión,
donde
es la matríz de transformación homogénea
(reducida, puesto que no contiene información de la componente z con lo cual quedaría
de tamaño 4x4 [14]) entre el sistema {A} y el cuerpo {0}, y T
es la matriz de transformación entre el
sistema {B} y el sistema {A}. Ambas matrices se evalúan teniendo en cuenta que
entre ellos existe una rotación alrededor del eje z seguida por una traslación
alrededor del eje x, es decir,
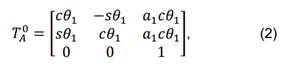
donde 𝑠𝜃𝑖 = sin(𝜃𝑖), 𝑐𝜃𝑖𝑗 = 𝑐𝑜𝑠(𝜃𝑖 + 𝜃𝑗), a1 y a2 son las longitudes de los eslabones, Fig. 1. Las posiciones (1,1), (1,2), (2,1) y (2,2) contienen la información de la orientación del elemento mientras que las posiciones (1,3) y (2,3) contienen la información de la posición. Para el caso de 𝑇𝐵 𝐴 queda la expresión (3). Realizando la multiplicación de (1) se obtiene la matriz de transformación en el marco fijo dada en (4), donde 𝑐𝜃𝑖 = cos(𝜃𝑖), 𝑐𝜃𝑖𝑗 = cos(𝜃𝑖 + 𝜃𝑗).
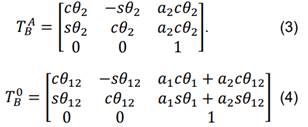
2.2 Cinemática Directa
El análisis cinemático directo tiene por objetivo calcular la posición del extremo del robot, lugar en donde se coloca la herramienta o efector final, teniendo en cuenta los movimientos articulares de cada junta. En el caso del robot de dos eslabones, las rotaciones de cada junta vienen especificadas por los ángulos 𝜃1 y 𝜃2 . La posición del extremo del robot en el marco fijo {0}, se define por sus coordenadas cartesianas mediante
donde 𝑟𝑥 es la componente x del extremo y 𝑟𝑦 es la componente y del extremo, las cuales se calculan directamente de la matriz de transformación homogénea reducida presentada en (2) a partir de sus elementos (1,3) y (2,3), respectivamente:
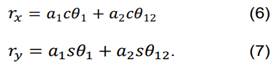
2.3 Cinemática Inversa
El
análisis cinemático inverso tiene por objetivo el calcular los desplazamientos
articulares o ángulos de cada junta del robot, 𝜃1 y 𝜃2 , a partir
de la información de posición del efector final 𝑷
. Para el robot de la Fig. 1 esto se consigue
despejando algebraicamente para los ángulos 𝜃1 y 𝜃2 a partir de
las expresiones (6) y (7), estas se reorganizan como se presenta en (8) y (9),
respectivamente.
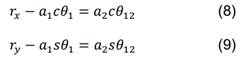
Las ecuaciones (8) y (9) son elevadas al cuadrado y sumadas para obtener la expresión (10), que se reordena como se presenta en (11). A continuación, se utilizan las identidades de la tangente del ángulo medio [15] mostradas en (12).
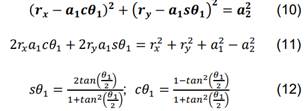
La
sustitución de (12) en (11) genera la ecuación cuadrática en (13), donde 𝐸1 =(𝑟
+ 𝑟
+ 𝑎
− 𝑎
)⁄2𝑎1. Las dos
soluciones de la ecuación (13) en θ1 están dadas por (14)
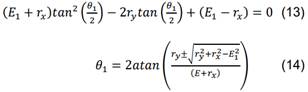
El
ángulo faltante 𝜃2 se obtiene
devolviéndose a (8) y (9), y reescribirlas para dejar los términos 𝑐𝜃1 y 𝑠𝜃1 en el lado
derecho. Son elevadas al cuadrado las ecuaciones y sumadas término a término,
para posteriormente utilizar las identidades de (12) y obtener (15), donde 𝐸2 = (𝑟 + 𝑟 +𝑎 −𝑎)⁄2𝑎2. Es aparente de (14)
y (15) que existirán dos configuraciones conocidas como codo arriba y codo abajo,
Fig. 2, dependiendo de la escogencia del signo en las opciones ±. La
configuración codo arriba, por ejemplo, se obtiene al escoger la combinación de
signos (+) para 𝜃1 , y (-) para 𝜃2
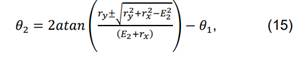
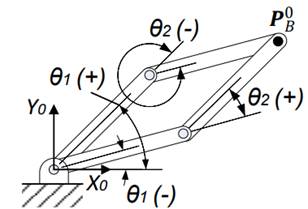
Fig. 2. Soluciones codo arriba y codo abajo del 2R
2.4 Planificación de la trayectoria
El desempeño de las tareas cinemáticas típicas de un robot serial, tales como corte de material [16], paletizado [17], soldadura [18], reparación de piezas [19], ensamble [20], movimiento de piezas [21] y pintura y recubrimientos [22], [23], [24], [25], [26], entre otras, requiere del conocimiento de la trayectoria a ser descrita por la herramienta. Se debe establecer una manera sistemática de programar el movimiento entre dos puntos, uno de partida y otro de llegada. Las trayectorias más comunes que se utilizan son el movimiento lineal y el movimiento circular, ambos pueden ser divididos en tres fases: una fase inicial de aceleración de cero hasta una velocidad máxima, una fase de velocidad constante y una última fase de desaceleración desde la velocidad máxima hasta velocidad cero, con finalización en el punto deseado de llegada. Se presenta a continuación la planificación de trayectoria, extraída de [27] y [28].
2.5 Variable Planificada
La variable planificada es aquella que cambia desde cero a un valor máximo dependiendo del movimiento. En el caso del movimiento lineal será la distancia entre los dos puntos, dmax. Para el caso del movimiento circular, la variable planificada es el ángulo de la rotación, θmax, alrededor del eje z. Para calcular las ecuaciones que determinan el valor de la variable planificada según el tiempo de simulación en cada fase (aceleración, velocidad constante, desaceleración) se procede a especificar las condiciones de frontera de cada tramo.
2.5.1 Tramo de aceleración.
Tiene una duración de 𝑡1 = 𝑡0, hasta 𝑡1 = 𝑡0 +𝑡𝑎𝑐𝑒𝑙, donde 𝑡𝑎𝑐𝑒𝑙: tiempo deseado que dure el proceso de aceleración, 𝑡0: tiempo inicial del movimiento. Posición: Inicial conocida: Punto actual de la herramienta robot, por lo que d y θ empiezan desde cero. Final conocida: es la distancia o el ángulo deseado del movimiento. Velocidad: Inicial conocida: Representada por 𝑑̇ , se considera que el movimiento parte del reposo con velocidad cero. Final conocida: Velocidad máxima del movimiento Vmax, las unidades serán mm/s o grados/s. Aceleración: Representada por 𝑑̈, no es conocida, pero se puede considerar que es constante en el tramo del movimiento. Las ecuaciones cinemáticas de la variable planificada para este tramo están dadas por (16) a (18).
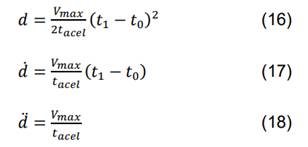
2.5.2 Tramo de Velocidad Constante. Tiene una duración de 𝑡2 = 𝑡0 + 𝑡𝑎𝑐𝑒𝑙 hasta 𝑡2 = 𝑡𝑓 − 𝑡𝑎𝑐𝑒𝑙, donde 𝑡𝑓: tiempo final de la simulación. Posición: Se representa por d, es variable, depende de la posición lograda en el tramo de aceleración más lo que se realice durante el movimiento. Velocidad: Representada por 𝑑̇, es constante e igual a la velocidad máxima permitida Vmax. Aceleración: Representada por 𝑑̈, es cero por ser un tramo a velocidad constante. Las ecuaciones de la variable planificada para este tramo están dadas por (19) a (21).
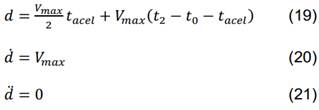
2.5.2 Tramo de desaceleración.
Tiene una duración de 𝑡3 = 𝑡𝑓 − 𝑡𝑎𝑐𝑒𝑙 hasta 𝑡3 = 𝑡𝑓. Posición: Se representa por d, es conocida y debe ser igual a 𝑑𝑚𝑎𝑥. Velocidad: Representada por 𝑑̇ , es variable y depende de la desaceleración y de la velocidad máxima 𝑉𝑚𝑎𝑥. Aceleración: Representada por 𝑑̈, es constante e igual al negativo del valor el primer tramo. Las ecuaciones cinemáticas de la variable planificada están dadas por (22) a (24).
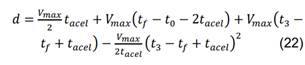
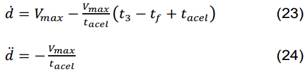
Teniendo en cuenta que para el tramo final la distancia recorrida es 𝑑𝑚𝑎𝑥 cuando 𝑡3 = 𝑡𝑓, se tieneentonces la expresión para el tiempo final en (25)
(25)
2.6 Algoritmo para la Variable Planificada
La variable planificada se calcula sistemáticamente de acuerdo con los siguientes pasos.
a) Solicitar al usuario el desplazamiento deseado, 𝑑𝑚𝑎𝑥, la velocidad máxima del desplazamiento, 𝑑̇𝑚𝑎𝑥, el tiempo inicial del movimiento, 𝑡0, el tiempo de aceleración, 𝑡𝑎𝑐𝑒𝑙.
b) Calcular el tiempo de duración del movimiento empleando la ecuación de 𝑡𝑓.
c) Identificar la etapa del movimiento: aceleración velocidad constante o desaceleración.
d) Calcular el desplazamiento 𝑑 según el tramo.
Para el robot plano existe una variable planificada para cada junta. Si el procedimiento anterior se realiza para cada una, estas se moverán a la velocidad máxima, terminando una junta antes que la otra. Usualmente en robótica se desea que el movimiento de todo el robot sea coordinado y para lograrlo se debe modificar la secuencia anterior en el paso b, dividido en pasos adicionales:
b.1 Calcular el tiempo de duración del movimiento, 𝑡𝑓, para cada articulación o junta.
b.2 Tomar el valor más alto de 𝑡𝑓 para recalcular las velocidades máximas de las juntas, 𝑉𝑚𝑎𝑥, para finalizar el movimiento simultáneamente.
2.7 Trayectoria Lineal
El movimiento lineal se describe por (26), donde 𝒑 es la posición actual del efector, 𝒑0 es su posición inicial, 𝒖 es el vector unitario que describe la dirección y sentido del desplazamiento, y 𝑑 es la variable planificada, en este caso es el desplazamiento del efector final.
2.8 Trayectoria Circular
El movimiento circular plano se considera una rotación alrededor del eje z, y el vector de posición deseada de un punto, 𝒑, se representa en función del centro del círculo, 𝒑𝑐 , el punto inicial de giro, 𝒑0, y del ángulo de giro, 𝜃, mediante (27), donde la variable planificada es 𝜃, que genera la matriz de rotación 𝑹𝑧(𝜃) alrededor del eje z.
2.9 Prototipo Real para Pruebas.
La Fig. 3 muestra el sistema mecatrónico construido. El diseño de los eslabones de aluminio de iguales dimensiones (50x10x210 mm entre centros, 0.28kg, e inercia de 10.3kg.cm2) se realizó con el workbench Mechanical Design del software DELMIA V5-6R2013. Los eslabones se fabricaron con fresadora Haas TMP1 empleando el código elaborado en el workbench CNC de DELMIA. Se usan dos motores idénticos Maxon Motors (ref. 310007), con reductor (ref. 166940) de 1:66, y un encoder (ref. 110512) de 500pulses/360° (pulsos por revolución). El conjunto motor-reductor de velocidad máxima 120rpm, tiene potencia nominal de 60W con par máximo de salida de 4N·m (suficiente para contrarrestar los torques de inercia y fricción de rodamientos) con corriente de 2A. El motor requiere del servoamplificador de control de posición EPOS2 24/2 marca Maxon Motors, que opera a 24V con máximo de 2A continuo y 4A en pico. El amplificador puede cuatriplicar la resolución del encoder, obteniendo en el eje de salida del reductor 132.000pulses/360° (pulsos de encoder por cada vuelta), es decir 366.67pulses/°
Fig. 3. Sistema mecatrónico de robot serial 2R
Para conectar el conjunto motor-encoder a los amplificadores EPOS2 se construyó la tarjeta que llevará el cableado del motor al cable plano de diez pines, por cuanto la alimentación del motor es separada a la conexión del encoder en el caso del motor, pero los EPOS2 requieren que todo esté en el mismo cableado. La Fig. 3.b ilustra el diseño de la PCB, que unifica ambos cableados.
3. RESULTADOS
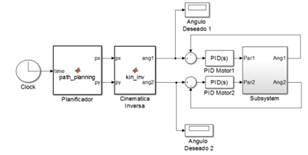
Los resultados obtenidos se generaron a partir de un control de posición por cinemática inversa del robot, ver Fig. 4(a). En este esquema de control se tiene un planificador, denominado “path_planning” el cual determina la posición deseada del robot según el tiempo transcurrido de la tarea. El planificador entrega el punto deseado en coordenadas cartesianas (𝑝𝑥,𝑝𝑦). A partir de este valor la cinemática inversa de posición calcula los valores correspondientes de los ángulos de giro de cada uno de los eslabones, para de esta forma poder alcanzar el punto deseado.
El resultado de la cinemática inversa de posición son los ángulos 𝜃1 y 𝜃2 , procedimiento realizado por el bloque “inv_kin”, Fig. 4(a). La posición articular deseada pasa por un lazo de control tipo PID que genera la señal de par para cada articulación. En la Fig. 4(b) se ilustra el bloque de SimMechanics que describe el sistema de dos barras. La entrada es el par ejercido por el motor en la junta y la salida es la posición angular de los motores. Este sistema se construye para imitar el sistema físico real y poder desde el entorno de simulación validar los movimientos del robot antes de las pruebas.
(a) Modelo en Simulink para pruebas
(b) Subsistema para la representación del robot
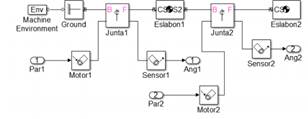
Fig. 4. Esquema de control para simulación
La Fig. 5(a) ilustra el sistema utilizado para mover el robot construido. Lo que cambia respecto a la figura 4(a) es que se han eliminado los PID por cuanto los EPOS2 lo poseen internamente. También se ha cambiado el bloque en SimMechanics por un bloque que se encarga de realizar la comunicación con los EPOS2. La entrada del bloque “Maxon Motors” es la posición angular deseada de los motores y la salida es la posición actual de la junta. La Fig. 5(b) ilustra el contenido del bloque “Maxon Motors”, hay dos bloques de transición de velocidades (ratetransition) para comunicación con el hardware de los EPOS2, ya que el bloque de comunicación corre a una velocidad diferente a la simulación en Matlab. Una ganancia convierte el valor angular deseado en pulsos de encoders utilizando la relación 366.67 pulses/°. La salida también es convertida de pulsos a grados. El bloque de Simulink que se comunica con los EPOS2 fue desarrollado por los autores [29], se encuentra disponible para consulta en [30].
(a) Modelo para control en tiempo real
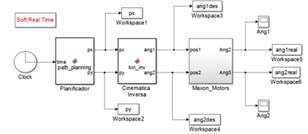
(b) Subsistema de comunicación con los EPOS2
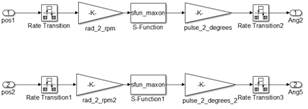
Fig. 5. Esquema de control del robot en tiempo real
3.1 Control de seguimiento del robot
La tarea a realizar por el robot se debe incluir en el código de la función embebida “path planning”. Se programaron tres tareas. La primera es un círculo, la segunda fue un triángulo y el último fue un cuadrado, las tres son ilustrativas de la capacidad del robot, y son típicas de las tareas cinemáticas más comunes de robot seriales: corte [16], soldadura [18] y pintura [22], [23].
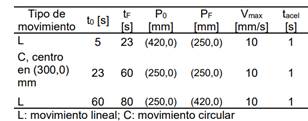
Tabla 1. Planificación de trayectoria para el círculo
3.1.1 Trazado de un Círculo.
El dibujo del círculo se planificó a partir de la posición HOME del robot, es decir cuando los ángulos tienen posición cero y el extremo del robot se ubica en la posición (420,0) mm. Para que el robot pueda seguir la trayectoria circular, se hace necesario recogerlo a un punto donde pueda girar dentro de su espacio de trabajo. El punto escogido fue el valor (250, 0) mm y a partir de allí se procede a girar en sentido horario los 360° teniendo como punto central el valor (300, 0) mm, es decir el radio del círculo es de 50 mm. Al finalizar la tarea se regresa el robot a su posición inicial (420, 0) mm. La tarea se divide en tres movimientos planificados, tal como se ilustra en la Tabla 1: línea recta, circulo y línea recta.
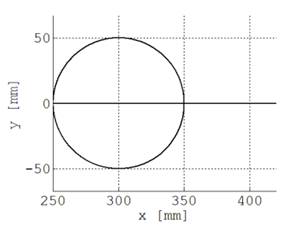
La Fig. 6 ilustra los datos de simulación del movimiento generados en el primer modelo en Simulink mostrado en la Fig. 4. La Fig. 6(a) incluye los tres movimientos planificados del efector final. En la Fig. 6.b se aprecia el resultado de la cinemática inversa, es decir llevar el movimiento planificado del efector final al movimiento articular de cada junta. Cuando se realizan las pruebas con el robot construido, se obtiene la diferencia entre la posición deseada y la posición actual de cada junta, Fig. 7, arrojando un error angular máximo inferior a 2.5°, y ocurre únicamente al inicio y final del movimiento.
3.1.2 Trazado de un Triángulo. El triángulo
también se dibuja a partir de la posición HOME. Las trayectorias involucran seis movimientos lineales, Tabla 2. El primer movimiento lleva la herramienta al punto inicial. Los otros cuatro movimientos dibujan los lados del triángulo. El último movimiento es para regreso a la posición HOME. La Fig. 8(a) ilustra el espacio de la tarea, y el espacio articular se muestra en la Fig. 8(b). Por otro lado, la Fig. 9 ilustra el error de seguimiento cuando la tarea se hace en tiempo real, no supera los 2.5°.
(a) Trayectoria Circular deseada del robot
(b) Ángulos de junta deseados
(b)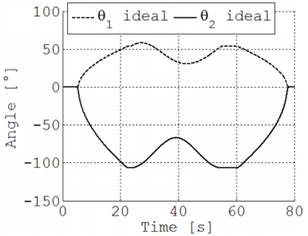
Fig. 6. Trayectoria y ángulos en pruebas del círculo
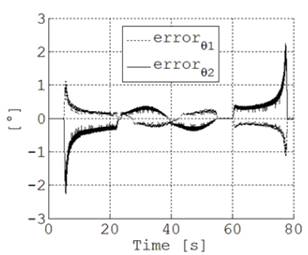
Fig. 7. Error angular en la generación del círculo
Tabla 2. Trayectoria planificada para el triángulo
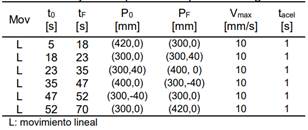
(a) Trayectoria triangular deseada del robot
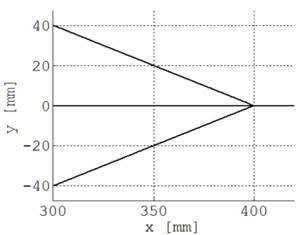
(b) Ángulos de junta deseados
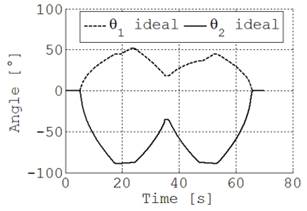
Fig. 8. Trayectoria y ángulos para el triángulo
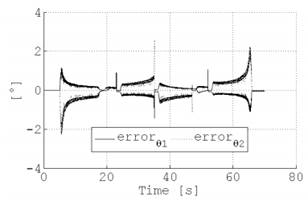
Fig. 9. Error angular en la generación del triángulo
3.1.3 Trazado de un Rectángulo.
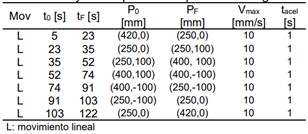
Para el caso del rectángulo se requieren siete movimientos lineales, Tabla 3, todos con una velocidad lineal de 10 mm/s y un tiempo de aceleración de 10 s. El rectángulo trazado se ilustra en la Fig. 10(a), mientras que los ángulos de junta reales se muestran en la Fig. 10(b). La Fig. 11 ilustra el error de seguimiento, inferior a 2.5°
Tabla 3. Trayectoria planificada para el rectángulo
4. INTERPRETACIÓN DE LOS RESULTADOS
La precisión del robot depende de la correcta posición y orientación del efector, logrado si los ángulos reales del robot coinciden con los ángulos calculados [31], [32]. Se calcula el error de posición de la herramienta, si se reemplazan los ángulos reales arrojados por los encoders en (6) y (7) para obtener las coordenadas reales en (28) y (29), donde el subíndice e indica valores arrojados por los encoders. Los errores de posición por componente, ex y ey, están dados para la herramienta por (30). El error total en la posición de la herramienta, e, se calcula con (31).
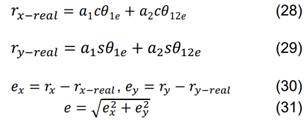
Si el trazado del círculo teórico presentado previamente, es contrastado con la posición real de la herramienta, se observaría la diferencia de trayectorias mostrada en la Fig. 12. La Fig. 13 complementa las diferencias en la trayectoria con la ilustración de los errores de posición en x, en y, y el error total. Se obtuvo un máximo error en la herramienta de 3.94 mm al inicio del movimiento, más no durante la generación del círculo en el cual el error no supera los 2 mm, aceptable para equipos de prototipado.
La explicación a esta diferencia se debe principalmente a que si bien se tiene un bloque para el control “soft-real time” siempre habrá una diferencia entre el tiempo de ejecución y el tiempo real del robot, lo que se transforma en una diferencia significativa entre el valor deseado y el valor actual del motor. Si bien este error se puede disminuir cambiando la velocidad de traslación por un valor menor, se optó por mostrar un resultado real ya que el objetivo del experimento es que los estudiantes aprecien el funcionamiento del controlador y sus limitaciones.
(a) Trayectoria rectangular deseada del robot
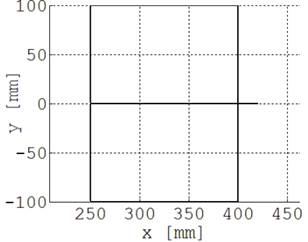
(b) Ángulos de junta deseados
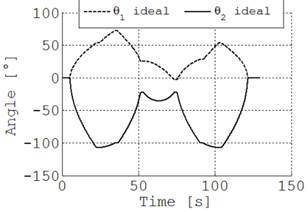
Fig. 10. Trayectoria y ángulos
para el rectángulo
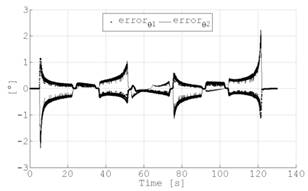
Fig. 11. Error en la generación del rectángulo
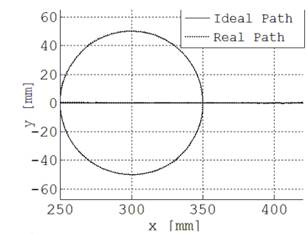
Fig. 12. Círculos ideal y real
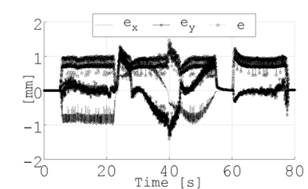
Fig. 13. Errores en la posición de la herramienta en la generación del círculo
5. CONCLUSIONES
En el presente artículo se ha realizado el análisis y control cinemático inverso de posición de un robot plano de dos grados de libertad conformado por dos eslabones. El robot fue satisfactoriamente controlado en posición utilizando el software comercial MATLAB y su entorno de control Simulink, tanto para simulación como para las pruebas. Para controlar cinemáticamente el robot se crearon funciones de planificación de la tarea que permitieran seguir trayectorias definidas con el robot. Las trayectorias creadas fueron formas básicas, pero de gran aplicación en la manufactura: un círculo, un triángulo y un rectángulo. Para cada una de las trayectorias diseñadas, el control cinemático se comportó adecuadamente, con errores de seguimiento en tiempo real no mayores a tres grados en cada junta.
Las tres trayectorias realizadas por el robot pueden tomarse como prácticas de una asignatura robótica a nivel de pregrado o posgrado. El interés de que los estudiantes puedan realizar prácticas con un robot físico radica en que pueden experimentar en la realidad para verificar los conceptos de cinemática y control. Esto repercute en el interés del estudiante, al ver que su programación puede pasar directamente de un entorno simulado a un entorno real, donde lo que se obtiene es idéntico a lo que ha programado. Si bien la experimentación se realizó con un hardware relativamente económico, el trabajo presenta completitud en los conceptos de cinemática y control cinemático o punto a punto, y constituye la base para posteriores prácticas de dinámica de manipuladores seriales.
6. AGRADECIMIENTOS
Este trabajo fue patrocinado por el Departamento de Investigaciones de la Universidad Tecnológica de Bolívar (Cartagena, Colombia) y COLCIENCIAS.
7 REFERENCIAS BIBLIOGRAFICAS
[1] Tsai, L., Robot Analysis: The Mechanics of Serial and Parallel Manipulators, Wiley Interscience, 1999.
[2] Lorenzo, B, Modelling and Control of Robot Manipulators, Springer, 2000.
[3] Corke, P., Robotics, Vision and Control: Fundamental Algorithms in MATLAB, Springer, 2013.
[4] Murray, R., Li, Z. y Sastry S., A Mathematical Introduction to Robotic Manipulation, CRC Press, 1994.
[5] Lucca, A., Lucibello, L., Panzieri S. y Ulivi, G. Control experiments on a two-link robot with a flexible forearm. Proceedings, 29th Conf. On Decision and Control. Honolulu, HI, 2, 520-527, December 1990.
[6] Berkemeier, M. y Fearing, R. Control of a twolink robot to achieve sliding and hopping gaits. Proceedings, IEEE Int. Conf. on Robotics and Automation. Nice, France, 286-291, May 1992.
[7] Tsao, T. y Safonov, M. Unfalsified direct adaptive control of a two-link robot arm. Proceedings, IEEE Int. Conf. on Control Applications. Kohala Coast, HI, 1, 680-686, August 1999.
[8] Kormushev, P., Demiris Y. y Caldwell, D. Encoderless position control of a two-link robot manipulator. Proceedings, IEEE Int. Conf. On Robotics and Automation. Seattle, WA, 943-949,May 2015.
[9] Schulte, H. y Guelton, K. Modelling and simulation of two-link robot manipulators based on Takagi Sugeno fuzzy descriptor systems. Proceedings, IEEE Int. Conf. on Industrial Technology. Mumbai, India, 2692–2697, December 2006.
[10] Wei, Y., Zhang, J., Hou, L., Jia, F. y Chang, Q. Backstepping Adaptive Fuzzy Control for Two-Link Robot Manipulator, Int. J. of Comp. Science Issues, 10(1), 303-308, 2013.
[11] Chen, C., Wu, T. y Peng, C. Robust Trajectories Following Control of a 2-Link Robot Manipulator via Coordinate Transformation for Manufacturing Applications, J. Robotics and Computer-Integrated Manufacturing, 27(3), 569- 580, 2011.
[12] Weinreb, A. y Bryson, A.-Jr. Minimum-Time Control of a Two-Link Robot Arm, Annual Review in Automatic Programming, 13(2), 195-199, 1985.
[13] Quanser 2-DOF Robot. Available on: http://www.quanser.com/products/2dof_robot [consulted on July 5, 2016].
[14] Crane, C.-III and Duffy, J., Kinematic Analysis of Robot Manipulators, Cambridge University Press, Cambridge, 2008.
[15] Norton, R., Diseño de Maquinaria: Síntesis y Análisis de Máquinas y Mecanismos, 4ta ed., McGraw-Hill, México, 2009.
[16] Choi, S. y Newman, W. Design and evaluation of a laser-cutting robot for laminated, solid freeform fabrication. Proceedings, IEEE Int. Conf. Of Robotics and Automation. San Francisco, CA, vol. 2, 1551-1556, April 2000.
[17] Mohd, N., Haron, H. y Mohamad, A. Robotic modeling and simulation of palletizer robot using Workspace5. Proceedings, IEEE Computer Graphics, Imaging and Visualization. Bangkok, Thailand, 217-222, August 2007.
[18] Andersen, R., Bogh, S., Moeslund, T. y Madsen, O. Intuitive task programming of stud welding robots for ship construction. Proceedings, IEEE Int. Conf. on Industrial Technology. Seville, Spain, 3302-3307, March 2015.
[19] Xiaoshu, J. y Xichen, Y. Off-Line Programming of a Robot for Laser Re-Manufacturing, J. Tsinghua Science and Technology, 14(S1), 186-191, 2009.
[20] Park, D., Park, C., Do, H., Choi, T. y Kyung, J. Development of dual arm robot platform for automatic assembly. Proceedings, Int. Conf. onControl, Automation and Systems. Gyeonggi-do, Korea, 319-321, October 2014.
[21] Sintov, A. y Shapiro, A. Automatic design algorithm of a robotic end-effector for a set of sheetmetal parts. Proceedings, IEEE 7th Int. Conf. On Cybernetics and Intelligent Systems. Siem Reap, Cambodia, 19-24, July 2015.
[22] Chen, H., Sheng, W., Xi, N., Song, M. y Chen, Y. Automated robot trajectory planning for spray painting of free-form surfaces in automotive manufacturing. Proceedings, IEEE Int. Conf. On Robotics and Automation. Washington, DC, vol. 1, 450-455, May 2002.
[23] Kuhlenkotter, B., Scheele, C. y Hypki, A. Realization of the thermal coating and mechanical compacting processes based on industrial multi robot systems. Proceedings, Robotics ISR/ROBOTIK. Munich, Germany, 1-7, June 2010.
[24] Tang, Y. y Chen, W. Tool trajectory planning of painting robot and its experimental. Proceedings, Int. Conf. on Mechatronics and Control. Jinzhou, China, 872-875, July 2014.
[25] Chen, H. y Xi, N. Automated Tool Trajectory Planning of Industrial Robots for Painting Composite Surfaces, Int. J. Advanced Manufacturing Technology, 35(7), 680-696, 2008.
[26] FANUC Painting and Coating Robots. Vailable on: http://www.autocells.com/painting-and-coatingrobots-by-fanuc [consulted on July 5, 2016]. [27] Jazar, R., Theory of Applied Robotics: Kinematics, Dynamics and Control, Springer, New York, USA, 2007.
[28] Spong, M., Hutchinson, S. y Vidyasagar, M., Robot Modeling and Control, 1st ed., Wiley New York, USA, 2005.
[29] Yime, E., Toolbox para el uso de controladores EPOS2 en Matlab, 2015, Colombia, Certificado de Registro de Soporte Lógico-Software No. 13-49- 394, 30 de septiembre de 2015 (aplicación).
[30] MathWorks File Exchange. Commanding Maxon Motors EPOS2 Motor Controller from MATLAB. Available in: https://www.mathworks.com/matlabcentral/fileexcha nge/53735-commanding-maxon-motors-epos2- motor-controller-from-matlab [consulted on July 5, 2016].
[31] Wu, C. The kinematic error model for the design of robot manipulator. Proceedings, American Control Conference. San Francisco, CA, 497-502, June 1983.
[32] Veitschegger, W. and Wu, C.H. Robot Accuracy Analysis based on Kinematics. IEEE J. of Robotics and Automation, RA-2(3), 171-179, 1986.