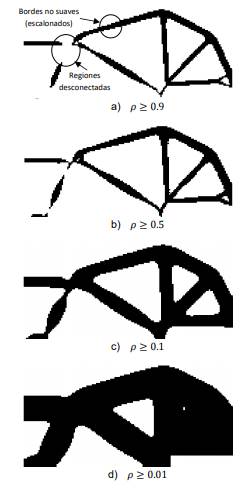MECANISMOS
FLEXIBLES: DESDE EL DISEÑO CONCEPTUAL
HASTA SU
MANUFACTURA
Francisco
Javier Ramírez Gil1, Esteban Sepúlveda Orozco2, Wilfredo
Montealegre Rubio3
Grupo
de Diseño y Optimización Aplicada (DOA, www.doa-unal.co), Departamento de
Ingeniería Mecánica, Facultad de Minas, Universidad Nacional de Colombia,
Medellín – Colombia.
1MSc
fjramireg@unal.edu.co,
2MSc
esepulvo@unal.edu.co
3DSc
wmontealegrer@unal.edu.co
RESUMEN
Los
mecanismos flexibles (MFs) son estructuras monolíticas donde su desplazamiento
se da gracias a la flexibilidad de sus miembros estructurales. Esto hace que
los MFs presenten ciertas ventajas en comparación con sus homólogos, los
cuerpos rígidos, tales como no requerir de lubricación ni ensamble. Este
trabajo muestra una metodología sistemática para la producción de un MF tipo
pinza, desde el diseño conceptual hasta su manufactura. Para el diseño del MF
se usa el método de optimización topológica (MOT), el cual permite diseñar
estructuras óptimas de forma automática distribuyendo una cantidad de material
dada dentro de un dominio de diseño especifico buscando maximizar el
desplazamiento en un punto. Al diseño obtenido mediante el MOT se le aplican
una serie de operaciones tendientes a disminuir la complejidad de la geometría obtenida
con el fin de reducir los costos de manufactura. Con la metodología propuesta
se obtiene un MF óptimo, funcional y con geometría innovadora.
Palabras
clave: Mecanismos
flexibles, diseño sistemático, optimización estructural, método de optimización
topológica (MOT), método de elementos finitos (MEF).
Recibido:
01 de diciembre de 2016 Aceptado: 12 de Junio de 2017
Received:
December 01th, 2016 Accepted: June 12th, 2017
COMPLIANT
MECHANISMS: FROM THE CONCEPTUAL DESIGN TO THEIR MANUFACTURE
ABSTRACT
The
compliant mechanisms (CMs) are monolithic structures where the displacement is
given by the flexibility of their structural members. Thus, the CMs show
certain advantages compared with their counterparts, the rigid bodies; since
assembling or lubrication are not required. This paper presents a systematic
methodology to produce a gripper-type CM, from the design to their manufacture.
For designing the CM, the topology optimization method (TOM) is used, where
optimal structures are automatically designed by distributing a given amount of
material within a specified design domain seeking for maximizing the
displacement at a point. Next, a series of operations are applied to the TOM
design for reducing the geometry complexity and then manufacturing costs. With
the proposed methodology, an optimal and functional CM with innovative geometry
is obtained.
Keywords:
Compliant
mechanisms, systematic design, structural optimization, topology optimization
method (TOM), finite element method (FEM).
Cómo
citar este artículo: F. J. Ramírez-Gil, E. Sepúlveda-Orozco, W.
Montealegre-Rubio, “Mecanismos flexibles: desde el diseño conceptual hasta su
manufactura,” Revista Politécnica, vol. 13, no. 24, pp. 65-78, 2017.
1.
INTRODUCCIÓN
Un
mecanismo flexible (MF) es una estructura monolítica flexible que entrega un
movimiento deseado bajo la acción de una fuerza [1]. Estos mecanismos se
diferencian de sus contrapartes, los mecanismos rígidos (MR), en que el
movimiento se da gracias a la deformación de los elementos que lo componen,
mientras que en los MR, el único movimiento es el que se consigue en las
juntas, ya que sus elementos se consideran infinitamente rígidos. Además,
mientras en los MR cada componente tiene una función diferente, los MFs pueden
integrar diferentes funciones en una o en un número reducido de partes [2].
Los
MFs presentan diferentes ventajas tales como [2]: mayor rendimiento ya que
ofrece alta compactibilidad y precisión, bajo peso y fricción, y eliminación de
la lubricación; costo más bajo debido al poco número de componentes, traducido
en una fabricación simplificada (pocos moldes), menor complejidad del
ensamblaje y reducción del stock; y su capacidad de miniaturizarse, es decir,
es posible su fabricación en la escala micro y nano (MEMS y NEMS [3]).
Adicionalmente, otra de las ventajas que presentan los MFs es que son
considerados diseños bio-inspirados [2]. Nótese que en la naturaleza, la mayoría
de objetos que se mueven son muy flexibles, tales como el tallo de las plantas,
las alas de los insectos, las anguilas, la trompa de los elefantes y otros
tantos ejemplos donde el movimiento proviene de la flexión de las partes [4].
El
uso de MFs se ha incrementado en los últimos años por su versatilidad [5], [6],
hecho que se evidencia en la gama de aplicaciones industriales que van desde
dispositivos de alta precisión en la micro-escala, a grandes componentes de
máquinas [7], [8]. Entre los factores que han influido para aumentar la
popularidad de los MFs es el desarrollo de nuevos materiales, técnicas de
diseño y procesos de manufactura [2]. Además, debido a las crecientes mejoras
en hardware y software, el diseño y análisis de MF ha aumentado en cantidad de
herramientas disponibles y complejidad abordada [5].
A
pesar de todas las potenciales ventajas que presentan los MFs, éstos también
experimentan dificultades. Una de las principales desventajas de los MFs es la
falla por fatiga, la cual proviene del movimiento de flexión repetido que puede
causar que el MF se dañe a una temprana edad de servicio.Por otro lado, el
movimiento en MF es másrestringido que en su contraparte y su diseño puede ser
más complejo. Además, debido a que los MFs son relativamente nuevos en
comparación con los MR, es difícil para los diseñadores encontrar recursos que
los guíen en su labor. Aunque existe suficiente literatura para ayudar a dichos
diseñadores a entrar en profundidad sobre temas relacionados con MFs, se
necesita de recursos más prácticos desde el punto de vista ingenieril, esto es,
recursos visuales y concisos que proporcionen inspiración y orientación en la
etapa conceptual de su diseño [2]. En consecuencia, se ha realizado un esfuerzo
considerable en la creación de métodos genéricos y sistemáticos para facilitar
su diseño.
Una
técnica para diseñar sistemáticamente MFs, que ha sido ampliamente acogida
tanto en la academia como en la industria, es el método de optimización
topológica (MOT). El MOT es un método computacional que permite diseñar estructuras
óptimas de forma automática, distribuyendo una determinada cantidad de material
en el interior de un dominio de diseño predeterminado con el fin mejorar su
desempeño frente a un fenómeno físico considerado [9]. La principal ventaja del
MOT es que no es necesario contar con una forma preliminar del diseño, lo cual es
bastante importante para los diseñadores novatos o para diseños que son
altamente complejos en donde es difícil obtenerlo por metodologías tradicionales
[10]. Adicionalmente, el MOT puede generar soluciones novedosas y/o puede ser utilizado
para ampliar la experiencia y la intuición del diseñador [2]. Sin embargo, el
resultado que arroja el MOT debe ser considerado como un primer bosquejo del
diseño conceptual, lo cual implica que se requiere una posterior interpretación
del diseñador y un posible posprocesamiento para corregir los defectos del
resultado del método [11].
Consecuentemente,
este trabajo presenta una metodología sistemática para la producción de un MF
tipo pinza, desde el diseño conceptual hasta su manufactura. Dicho trabajo
muestra el cómo encajar “nuevas” herramientas de diseño como el MOT y “nuevas” tecnologías
como la manufactura aditiva (MA), en metodologías de diseño tradicional. Para lograr
este objetivo, a los diseños obtenidos mediante el MOT se les aplica una serie
de operaciones de posprocesamiento tendientes a reducir la complejidad de la
geometría y de esta forma disminuir los costos de manufactura.
Adicionalmente,
se verifica el diseño mediante el método de los elementos finitos (MEF) y se
procede a la fabricación del mismo por MA. Finalmente, se hace una comparación
del desempeño del MF desde el diseño dado por el MOT, del mejorado por el diseñador
(interpretado) y del fabricado.
2.
MATERIALES
Y METODO
Debido
a que el diseñador es el responsable de las características técnicas y
económicas de un producto, y a la importancia comercial del desarrollo de
productos de forma oportuna y eficiente, es importante contar con un
procedimiento de diseño definido para hallar las soluciones. Este procedimiento
debe ser flexible y al mismo tiempo ser capaz de ser planificado, optimizado y verificado.
Sin embargo, este procedimiento puede no ser efectivo si el diseñador no tiene
el conocimiento necesario y/o no puede trabajar de manera sistemática [10].
Este procedimiento sistemático es conocido como metodología de diseño.
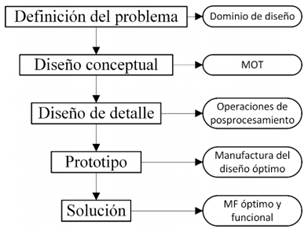
Fig. 1. Modelo de diseño de
Pahl y Beitz adaptado al diseño de MFs mediante el MOT.
Dentro
de las metodologías de diseño se encuentran los modelos, los cuales dictan los
pasos a seguir en el diseño. Algunos modelos simplemente describen la secuencia
de actividades que ocurren típicamente en el diseño, mientras que otros modelos
intentan prescribir un mejor o más adecuado patrón de actividades [12]. Estos
modelos a pesar de ser sistemáticos, son heurísticos, es decir, se basan en la
experiencia previa del diseñador y en directrices y reglas prácticas que
conducen a lo que el diseñador espera ser la dirección correcta, pero sin
garantía absoluta de éxito [12]. Por lo tanto, con el fin de sistematizar el
diseño de MFs, en este trabajo se usa el modelo de diseño de Pahl y Beitz [10],
como se ilustra en la Fig. 1, donde el problema consiste en diseñar una
estructura flexible, sujeta a cargas y condiciones de frontera, que se desplace
lo máximo posible en un punto específico. A fin de disminuir la heurística del
proceso de diseño, se usa el MOT para conseguir el diseño conceptual del MF.
Luego se siguen una serie de operaciones que constituyen el diseño de detalle.
Una vez completada la tarea anterior, el diseño está listo para ser
manufacturado, lo que finalmente completa la solución al problema de diseño. En
las siguientes subsecciones se detalla el procedimiento seguido en este trabajo
al usar el modelo de diseño de Pahl y Beitz.
2.1
Definición
del problema de diseño
En
este trabajo se quiere diseñar un MF tipo pinza, el cual es comúnmente usado
para labores de manipulación en áreas de la salud y en mecánica de precisión
[13], [14]. El dominio de diseño del cual se parte se presenta en la Fig. 2. El
dominio de diseño es el espacio permitido para el diseño del MF (región donde
el MOT puede redistribuir el material), el cual consta de geometría y
condiciones de frontera. Adicionalmente, a este dominio se le pueden predefinir
zonas sólidas o vacías, las cuales no pueden ser modificadas por el MOT
(regiones de no diseño). Con el propósito de disminuir el costo computacional
asociado al MOT, se considera simetría respecto al eje X, y se usa un dominio bidimensional
(que es equivalente a diseñar la sección transversal de una estructura 3D). El
análisis de la estructura se realiza mediante el MEF con la teoría de esfuerzo
plano.
2.2
Diseño
conceptual del MF mediante el MOT
El
diseño de MFs mediante el MOT se puede formular de diversas maneras, pero no
hay todavía una formulación definitiva que sea universalmente aceptada [2].
Para una comparativa entre diferentes formulaciones se puede consultar la
referencia [15]. De forma general, se puede encontrar dos enfoques para el
diseño sistemático de MFs basados en el MOT: el enfoque cinemático (usado por
ejemplo en [16]) y el enfoque continuo (usado por ejemplo en [17]). En el
primer enfoque, el dominio de diseño continuo se aproxima mediante una densa
red de elementos finitos (EFs) unidimensionales (1D) tipo truss o beam,
mientras que la aproximación basada en el continuo normalmente utiliza un
dominio de diseño continuo discretizado en EFs bidimensionales (2D) o
tridimensionales (3D). Mediante el uso de una malla fina, el segundo modelo
representa mejor el medio continuo, y por lo tanto, es la aproximación empleada
en este trabajo.
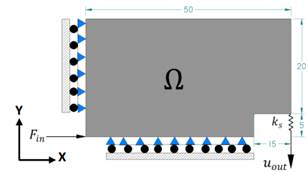
Fig. 2. Dominio de diseño 2D
para un MF tipo pinza considerando simetría con respecto al eje X (medidas en
mm).
Por
otro lado, la aproximación basada en el continuo dispone de diferentes enfoques
para parametrizar el dominio de diseño. Los más conocidos y mejor desarrollados
son el SIMP (solid isotropic material with penalization) y el método de
homogenización [18]. El método SIMP consiste en asignar a cada EF una variable
de diseño, comúnmente llamada pseudo-densidad, la cual puede tomar valores
entre cero (EF sin material) y uno (EF con material). El método de
homogenización produce topologías similares en apariencia a las obtenidas con
el SIMP, pero es más complicado ya que requiere de más variables de diseño y
mayor tiempo de cómputo [2]. Por lo que se opta por usar el SIMP en este
trabajo (la mayoría de los softwares comerciales usan este modelo de material
en sus implementaciones). Finalmente, para la solución del problema de optimización
se usa a técnica de programación lineal secuencial (PLS), por su generalidad
(capaz de resolver problemas no lineales, multifísicos, etc.) y eficiencia para
resolver problemas con un gran número de variables de diseño.
La
Fig. 3 muestra el diagrama de flujo empleado para diseñar MFs mediante el MOT usando
PLS. Se parte de un dominio de diseño, el cual es discretizado con EFs, usando
una malla estructurada o no dependiendo de la complejidad de dicho dominio.
Seguidamente se resuelve el problema elástico mediante el MEF. Debido a que la PLS
resuelve sub-problemas lineales en cada iteración del MOT en forma secuencial,
tanto la función objetivo como las restricciones deben ser lineales. La
linealización se logra mediante series de Taylor de primer orden y se conoce
como análisis de sensibilidad, el cual consiste en calcular la primera derivada
de la función objetivo con respecto a cada variable de diseño. Por otro lado,
en la PLS se debe limitar el espacio de solución de cada variable de diseño, lo
cual se logra mediante el uso de los límites móviles. Luego de esto se debe
aplicar un filtro con el fin de controlar la complejidad de la topología resultante
[19]; es decir, para evitar la aparición de miembros estructurales muy
pequeños, escala de grises y tablero de ajedrez [20], que hacen de la manufactura
un proceso difícil y costoso. Después se procede con la solución del
sub-problema lineal de optimización mediante el método de punto interior [21].
A partir de este punto se verifica el cumplimiento de algunos criterios de
convergencia, realizando iterativamente el procedimiento anterior hasta
alcanzarlos. Finalmente, si el resultado converge, la topología óptima es
graficada en una escala de grises.
En
este trabajo, la programación del MOT usando PLS se realiza en MATLAB®. Las
geometrías usadas son simples y por tal motivo se realizan y discretizan en
este software con mallas estructuradas. El MEF estático lineal es programado usando
EFs Q4 y el análisis de sensibilidad se realiza por el método adjunto [22].
Para los limites móviles se usa una regla heurística descrita en [23]. Por otro
lado, el filtro usado es el filtro espacial AWSF propuesto en [19]. Este filtro
es aplicado sobre los límites móviles con la ventaja de que los posibles
valores que puede tomar la pseudodensidad de cada EF esté relacionada con los
EFs vecinos, lo cual implica que 𝜌𝑒 no difiere mucho de sus
vecinos, disminuyendo el tablero de ajedrez y la dependencia del resultado con
la malla [20]. El tablero de ajedrez se genera cuando la variable de diseño en
una región varía entre 1 y 0 creando una rigidez ficticia [9]. Finalmente, el
criterio de convergencia en el algoritmo de optimización se basa en el valor de
la función objetivo 𝑢𝑜𝑢𝑡 de las últimas
tres iteraciones 𝑘, 𝑘 − 1 y 𝑘 − 2, donde
se mide si hay o no mejoramiento de dicha función siguiendo la siguiente regla
[24]:
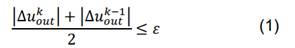
donde
Δ𝑢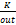 = 𝑢
= 𝑢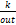 − 𝑢
− 𝑢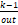 , Δ𝑢
, Δ𝑢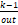 = 𝑢
= 𝑢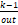 − 𝑢
− 𝑢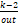 y 𝜀 es una tolerancia dada,
normalmente una fracción de la función objetivo cuando la estructura está completamente
sólida. Si la tolerancia no se alcanza antes de un número máximo de iteraciones
𝑘𝑚𝑎𝑥, entonces
el algoritmo termina. En las siguientes subsecciones se presenta el problema de
optimización topológica aplicado al diseño de MFs y el modelo de material SIMP.
y 𝜀 es una tolerancia dada,
normalmente una fracción de la función objetivo cuando la estructura está completamente
sólida. Si la tolerancia no se alcanza antes de un número máximo de iteraciones
𝑘𝑚𝑎𝑥, entonces
el algoritmo termina. En las siguientes subsecciones se presenta el problema de
optimización topológica aplicado al diseño de MFs y el modelo de material SIMP.
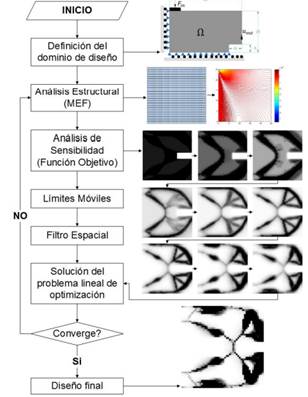
Fig. 3. Algoritmo del MOT usando PLS aplicado
al diseño de MFs.
2.2.1
Formulación del problema de optimización
El
problema de optimización para el diseño de MFs se formula teniendo en cuenta
una carga estática 𝑭 aplicada externamente a la estructura capaz de deformarla
y generar un desplazamiento máximo 𝑢𝑜𝑢𝑡 en cierto
punto de ella. Luego, el problema de optimización en forma discreta se presenta
en la Ec. (2), donde 𝝆 es el vector de
variables de diseño, 𝑳 es un vector de ceros
con el valor de uno en la posición del grado de libertad (GDL) que se quiere maximizar
del vector de desplazamientos 𝑼, obtenido a partir del
MEF. La primera restricción del problema de optimización es la ecuación de equilibrio,
siendo 𝑲(𝝆) la matriz
de rigidez, la cual depende de las variables de diseño debido al modelo de
material SIMP [18], descrito en la sección 2.2.2. La segunda restricción
asegura que la topología final tenga un volumen 𝑉∗inferior al
volumen total del domino de diseño 𝑉𝑡, donde 𝑣𝑒 es el
volumen del EF𝑒, el término
𝑛𝑒𝑙 indica el
número total de EFs usados en la discretización de dicho dominio y 𝑓 es una
fracción (0 < 𝑓 < 1). Finalmente, la tercera restricción se
conoce como límites móviles, los cuales controlan la solución, donde 𝜌𝑒𝑙
y
𝜌𝑒𝑢
son
el límite móvil inferior y superior de la variable de diseño 𝜌𝑒
,
respectivamente.
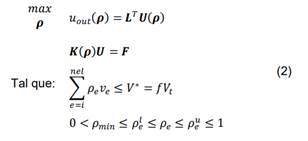
Los
supuestos que están implícitos en este enfoque son un comportamiento elástico
lineal del material y pequeñas deformaciones en la estructura. Para controlar
la rigidez del MF resultante y grandes valores para 𝑢𝑜𝑢𝑡 que
resultaría en no linealidades geométricas, el MF se diseña considerando que en este
punto existe una resistencia al libre movimiento, modelado como un resorte (ver
Fig. 2), de tal forma que la rigidez de dicho resorte 𝑘𝑠 controla la
rigidez del MF [25]. Adicionalmente, el resorte sirve para “forzar” al
optimizador a conectar el material desde el anclaje hasta 𝑢𝑜𝑢𝑡 [2].
2.2.2
Modelo de material SIMP
El
modelo de material utilizado en este trabajo y uno de los más usados en la
implementación del MOT es el SIMP, el cual consiste en definir el valor de una propiedad
efectiva del material 𝐸𝑒 en cada uno
de los EFs del dominio discretizado 𝑥 en función de la pseudo-densidad
𝜌𝑒 y la
propiedad del material base
𝐸0 de la
siguiente manera [9]:
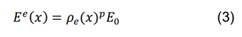
donde
𝜌𝑒 se
encuentra definida dentro del intervalo [𝜌𝑚𝑖𝑛, 1]. El
valor de 𝜌𝑚𝑖𝑛,
típicamente 10−3 , aparece con el fin de evitar inestabilidades numéricas en el
MEF e indica las partes estructurales sin significancia (vacio). Si 𝜌𝑒 = 1 se
tiene la propiedad del material base (𝐸 𝑒 = 𝐸0) y el EF
queda en la topología final (sólido). Los valores intermedios de 𝜌𝑒
generan
áreas gises en la topología, y por tanto, se usa el factor de penalización 𝑝 para
disminuir dicho efecto. Normalmente, se toma 𝑝 > 1 y 𝑝 < 10,
donde 𝑝 = 3 es un
valor típico.
2.3
Diseño
de detalle
Debido
a que normalmente la topología producida por el MOT no es apta para su
manufactura por la escala de grises presente y los bordes poco suaves, a ésta
se le deben realizar algunas operaciones de posprocesamiento, las cuales
conforman la etapa de diseño de detalle. La Fig. 4 ilustra los pasos seguidos
en esta etapa hasta conseguir un MF apto para manufacturar. El primer paso
consiste en hacer una interpretación del diseño conceptual obtenido a partir
del MOT. La interpretación consta en decidir qué valores de las
pseudo-densidades se considerarán, es decir, que EFs quedarán en la estructura
final, y cuáles no. Esto se hace ya que usando el SIMP se pueden obtener seudodensidades
entre 𝜌𝑚𝑖𝑛 y 1, donde
los valores intermedios significan cualquier material diferente del material
base y del vacío, es decir, forma una estructura con diferentes materiales, lo
cual es muy complicado de manufacturar a menos que se utilicen técnicas avanzadas
para la fabricación de materiales compuestos como los funcionalmente gradados [26].
uego de la eliminación de la escala de grises, se obtiene una topología bien
definida, solo con regiones blancas y negras (black and white design). Sin
embargo, como dicha topología proviene de una discretización con EFs
rectangulares, los contornos de ésta son poco suaves (dientes de sierra).
El
problema de los dientes de sierra en la topología se soluciona suavizando los
bordes. En la suavización de la topología se usa un software CAD, particularmente,
en este trabajo se usó Solidworks®. Para realizar este procedimiento, la
topología interpretada es guardada en un formato de imagen. Luego, esta imagen
es importada al CAD, la cual generalmente no tiene las dimensiones correctas, con
lo que es necesario escalarla a las medidas requeridas. Una vez escalada la
imagen, el diseñador suaviza los contornos manualmente con curvas spline.
Finalmente, dicho modelo 2D suavizado se extruye uniformemente una profundidad
igual al espesor con el fin de crear el modelo 3D, el cual queda listo para su
manufactura. Cabe anotar que en el intermedio de cada etapa se hace un análisis
mediante el MEF de la topología actual del MF. Este análisis se hace con el fin
de detectar elementos estructurales sometidos a grandes esfuerzos y donde el
esfuerzo supere el limite elástico del material (el MF no se desea deformar
permanentemente para poderlo usar varias veces), la estructura debe ser
modificada engrosando dichos elementos. También se pueden hacer cambios a la
estructura con el fin de favorecer su desempeño y/o eliminar características de
difícil manufactura.
2.4
Fabricación
del prototipo por manufactura Aditiva
La
topología óptima posprocesada se fabrica en ABS (acrylonitrile butadiene
styrene) usando una impresora 3D Fortus 400mc mediante la técnica FDM (fused
deposition modeling). En la manufactura aditiva (AM, por sus siglas en inglés),
impresión 3D o prototipado rápido [27] del prototipo mediante FDM se crea la
pieza capa por capa de abajo hacia arriba, calentando y extruyendo un filamento
de material termoplástico de nivel de ingeniería (ABS). Dicha tecnología se
suele emplear para generar geometrías complejas como las resultantes del MOT y
piezas funcionales como prototipos y piezas de producción de bajo volumen [28].
Adicionalmente, este proceso de manufactura es adecuado ya que reproduce
fácilmente la geometría intrincada del MF tipo pinza obtenido mediante el MOT y
evita el fabricar los costosos moldes requeridos por métodos de manufactura de
polímeros convencionales como moldeo por inyección, extrusión o soplado.
3. RESULTADOS Y
DISCUSIÓN
La
solución al problema inicialmente planteado (Sección 2.1), según el modelo de
diseño Pahl y Beitz (ver Fig. 1), se presenta en esta sección, mostrando los
resultados de las diferentes etapas.
3.1
Diseño
conceptual del MF tipo pinza
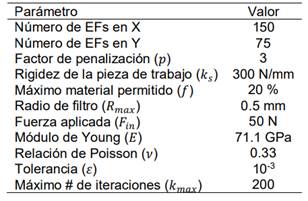
En
el MOT existen diversos parámetros de entrada los cuales afectan la topología
final, es decir, cada grupo de parámetros produce una topología diferente, por
lo que es común hacer un estudio de éstos y definir cuáles son los más
apropiados para un problema específico [23]. En la Tabla 2 se hace una
comparación considerando tres valores diferentes para el tamaño del filtro, la
calidad de la malla, la cantidad disponible y el tipo de material, la
rigidez
de la pieza de trabajo en el punto de salida, el valor inicial de las variables
de diseño y el número de iteraciones máximas permitidas. Cuando el parámetro no
varía, se considera el valor dado en la Tabla 1.
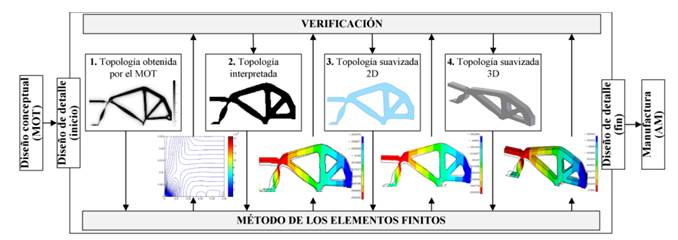
Fig. 4. Procedimiento seguido
en la etapa de diseño de detalle para el desarrollo de MFs mediante el MOT
Tabla
1.
Parámetros de diseño usados en el MOT.
De
la Tabla 2 se observa lo siguiente:
·
Cuando
no hay filtro (𝑅𝑚𝑎𝑥 = 0), el MOT
presenta problemas de tablero de ajedrez y miembros estructurales delgados,
pero un valor alto para 𝑅𝑚𝑎𝑥 (más de 8 EFs
dentro del radio de filtro) incrementa la escala de grises.
·
La
discretización es mejor entre más EFs se usen, ya que aumenta la definición de
los bordes y asegura la convergencia del MEF, pero el costo computacional
incrementa exponencialmente con el número de EFs [5]. No se observa
independencia de malla porque se usó el mismo tamaño de filtro en los tres
casos, lo cual implica que para el caso I (𝑛𝑒𝑙 = 1250) y II (𝑛𝑒𝑙 = 5000) no
actúa dicho filtro debido al tamaño del EF.
·
Si
𝑓 es pequeña, la
topología es similar a una estructura tipo cercha, pero si 𝑓 es grande, el
material es desperdiciado acumulándose en zonas que no aportan al desempeño del
MF.
·
Cuando
no se usa el artificio de un resorte en el GDL a maximizar, la topología es tan
flexible que alcanza desplazamientos irreales (𝑢𝑜𝑢𝑡 = −747.48 mm).
Por el contrario, cuando 𝑘𝑠 → ∞, 𝑢𝑜𝑢𝑡 → 0.
·
Debido
a que la PLS usa un valor inicial para 𝝆, el resultado depende
de cual se tome, y por ser un proceso iterativo, el resultado final es
distinto.
·
El
número máximo de iteraciones permitido es un compromiso entre el tiempo de
cómputo y la resolución de la topología, ya que para pocas iteraciones (𝑘𝑚𝑎𝑥 = 30) ésta aun
parece no estar definida y usando muchas iteraciones (𝑘𝑚𝑎𝑥 =500) la
ganancia es poca a costa de un tiempo adicional de simulación, que generalmente
es alto en comparación con un número intermedio de iteraciones (𝑘𝑚𝑎𝑥 = 200).
·
El
material no es influyente en la topología, ya que se comparó el módulo de Young
del ABS (𝐸 =20 𝑀𝑃𝑎) con el del
aluminio (𝐸 = 71.7 𝐺𝑃𝑎) y las diferencias
no son significativas haciendo una inspección visual a la topología. Esto
indica que se puede diseñar la topología de manera general con el MOT sin
incluir propiedades reales del material. De hecho, en la literatura se
encuentra que normalmente asumen un 𝐸 = 1 [29].
El
material no es influyente en la topología, ya que se comparó el módulo de Young
del ABS (𝐸 = 20 𝑀𝑃𝑎) con el del
aluminio (𝐸 = 71.7 𝐺𝑃𝑎) y las diferencias
no son significativas haciendo una inspección visual a la topología. Esto
indica que se puede diseñar la topología de manera general con el MOT sin
incluir propiedades reales del material. De hecho, en la literatura se
encuentra que normalmente asumen un 𝐸 = 1 [29].
La
Tabla 2 se asemeja al diagrama morfológico comúnmente usado en los modelos de
diseño tradicionales para la generación de alternativas de solución. De hecho,
en dicha tabla se presentan dos alternativas, la 1ª se identifica con líneas
punteadas, mientras que la 2ª con líneas sólidas. La selección de los
parámetros se basa en aquellos que producen la mejor topología en términos de
menor escala de grises, mejor definición de bordes y menor tiempo de cómputo.
Para el MF tipo pinza diseñado en este trabajo se selecciona la 1ª alternativa
(ver Fig. 5), aunque algunas regiones de la estructura poseen escala de grises.
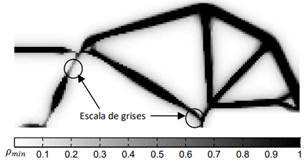
Fig.
5.
Topología óptima obtenida por el MOT.
La
Fig. 6 muestra la curva de convergencia de la función objetivo. Cuando el MOT
empieza su proceso iterativo, el desplazamiento en el punto de salida 𝑢𝑜𝑢𝑡 es
prácticamente igual a cero. Como el objetivo es maximizar 𝑢𝑜𝑢𝑡 en dirección
–Y cuando una fuerza en dirección horizontal 𝐹𝑖𝑛 (positiva del eje
X) es aplicada (ver Fig. 2), el MOT lo hace en las siguientes iteraciones.
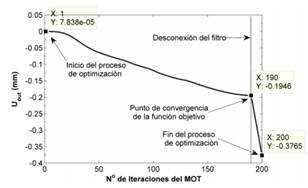
Fig. 6. Curva de convergencia
de la función objetivo.
En
la iteración 190 el MOT converge, ya que el valor de 𝑢𝑜𝑢𝑡 no cambia
significativamente en las tres últimas iteraciones. Cuando se alcanza la convergencia,
el MOT realiza 10 iteraciones más, pero con el filtro desconectado con el fin
de disminuir la escala de grises. Se observa una mejoría en la función objetivo
cuando el filtro se desconecta, ya que las regiones grises disminuyen. Las
zonas grises son consecuencia del SIMP y del filtro y es material compuesto
(con módulos de Young desde 7.17 × 10−5 𝑃𝑎 para los EFs
con 𝜌𝑒 = 𝜌𝑚𝑖𝑛 hasta 7.17 ×
109 𝑃𝑎 para los EFs
con 𝜌𝑒 = 1) que
aumenta la rigidez del MF. Por lo tanto, al eliminar estas zonas se espera que
la topología tenga mayor flexibilidad.
Tabla
2.
Estudio de variación de parámetros en el MOT para el diseño de un MF (diagrama
morfológico)
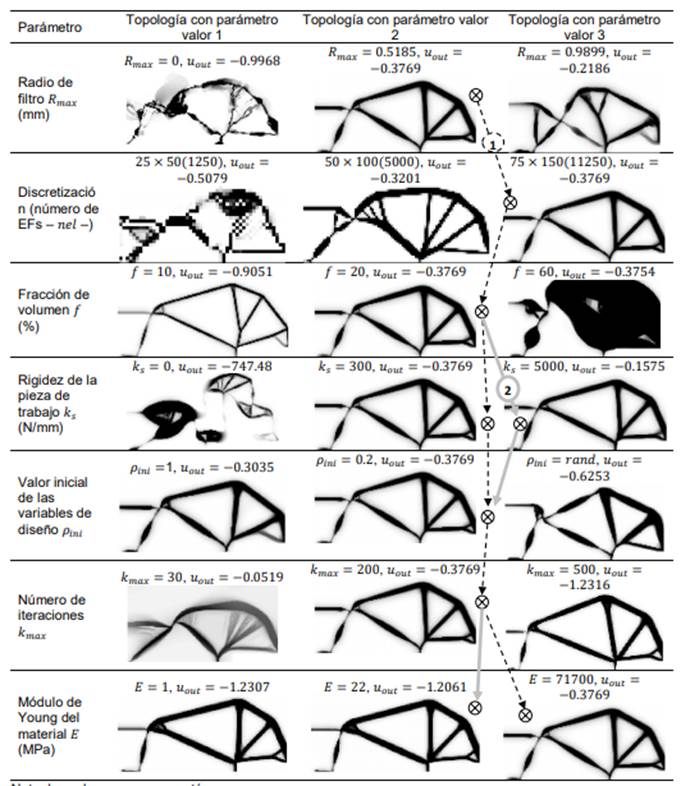
Nota: los valores para 𝑢𝑜𝑢𝑡 están en mm.
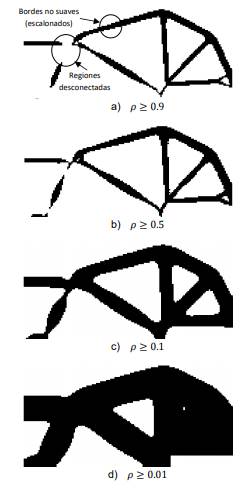
Fig. 7. Topologías con
posprocesamiento básico considerando diferentes valores de threshold.
3.2
Diseño
de detalle del MF tipo pinza
Un
procedimiento simple para eliminar la escala de grises es hacer que los EFs
cuyas pseudodensidades estén por debajo de un valor definido por el diseñador
(threshold) sean retirados del diseño, y los que estén por encima de ese valor
se consideran iguales a uno (1), es decir, llenos del material base (ver paso 1
al 2 en la Fig. 4). Este posprocesamiento es aplicado a la topología de la Fig.
5 y los resultados se muestran en la Fig. 7 donde se genera un diseño totalmente
definido (blanco/negro). Se observa que la topología queda con miembros
estructurales desconectados cuando threshold > 0.5. Por debajo de este valor
los miembros se conectan, además, se disminuye la complejidad de la geometría
ya que desaparecen algunos agujeros pequeños y los miembros de la estructura se
engruesan, lo cual significa que la manufactura es menos compleja y, por lo
tanto, menos costosa. Sin embargo, si se consideran los EFs con
pseudo-densidades muy pequeñas, los agujeros obtenidos por el MOT tienden a
desaparear y la estructura se vuelve más rígida, disminuyendo el desempeño del
MF.
Aunque
con el posprocesamiento básico se logra obtener diseños completamente
definidos, sus bordes no son suaves, lo cual representa un sobrecosto a la hora
de manufacturarlos, además de que pueden ser concentradores de esfuerzos. Estos
bordes en forma de escaleras (dientes de sierra) se eliminan mediante curvas suaves
a trozos como los splines, a pesar de que existen técnicas más avanzadas como
la optimización de forma, ésta incrementa la dificultad del diseño [30]. La suavización
de los bordes se realizó con el software Solidworks® mediante curvas splines de
forma manual (ver paso 2 al 3 en la Fig. 4). La Fig. 8a) muestra la topología
completa y suavizada, proveniente de la Fig. 7c), puesto que es la mejor definida,
sin problemas de miembros estructurales desconectados ni exceso de material.
Debido a la naturaleza 3D de los objetos en la vida real, la topología 2D
suavizada se le da un espesor de 3mm, obteniéndose la topología 3D como se
indica en la Fig. 8b) (ver paso 3 al 4 en la Fig. 4). Se observa que con este
posprocesamiento adicional sobre la topología (suavizado de bordes), la
complejidad de su manufactura se ha reducido aún más. Es por ello que el MOT se
considera una técnica para obtener ideas previas del diseño conceptual, ya que
por lo regular sus resultados requieren de la intervención posterior del diseñador
(diseño de detalle).
Con
el objetivo de verificar el desempeño de las topologías modificadas por los
posprocesamientos realizados, así como comparar y evaluar su desplazamiento en
el punto deseado (𝑢𝑜𝑢𝑡), éstas son simuladas
en el software comercial de elementos finitos ANSYS®, con las mismas suposiciones
realizadas en MATLAB® (análisis estático lineal y esfuerzo plano). La Fig. 9
muestra
los
desplazamientos nodales en dirección Y para los tres posprocesamientos
realizados a la topología original. La Fig. 9a) muestra la simulación de la topología
proveniente de la Fig. 7c) en donde se usó 11.250 EFs Q4 (PLANE42). La Fig. 9b)
muestra la simulación de la topología 2D suavizada (Fig. 8a), en donde se usó
una malla con 498.712 EFs PLANE42, la cual aseguró la convergencia del MEF. La
Fig. 9c) muestra la simulación de la topología 3D suavizada (Fig. 8b) usando
EFs prismáticos con tres GDL por nodo (SOLID45) con un total de 1.016.430 EFs, garantizando
la convergencia del MEF. En las tres simulaciones se comprueba que el
desplazamiento en el punto de interés (ver Fig. 2) es el máximo y en la
dirección adecuada, lo cual verifica el resultado del MOT.
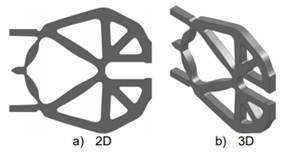
Fig. 8. Topología suavizada
mediante curvas splines (geometría completa del MF tipo pinza).
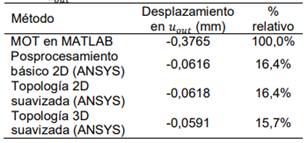
La
Tabla 3 muestra los valores numéricos de 𝑢𝑜𝑢𝑡 obtenidos a
partir de las simulaciones en ANSYS® y en donde se compara con el valor
original obtenido por el MOT en MATLAB®. En dicha tabla se observa que la
topología obtenida con el MOT en MATLAB® presenta un desplazamiento alto
comprado con los demás (considerado el 100%), lo cual se debe a que en los
posprocesamientos hubo un engrosamiento de los miembros estructurales, haciendo
más rígido al MF. Cuantitativamente, al eliminar por completo la escala de
grises de la topología original tomando todos los EFs cuyas pseudo-densidades
estén por encima de 0.1 (ver Fig. 7c), el desplazamiento disminuye aprox. un
84%. Consecuentemente, en los diseños blancos/negros a pesar de tener cambios
significativos como la forma de los contornos (suavizado de bordes) y/o de
aumento de la dimensión (2D a 3D), estos factores no parecen alterar
significativamente el desempeño del MF, lo que se ve reflejado en 𝑢𝑜𝑢𝑡. Por lo tanto,
con el fin de evitar un deterioro en el desempeño de las estructuras diseñadas
mediante el MOT al ser posprocesadas, es necesario usar técnicas que eliminen,
o por lo menos, disminuyan los EFs con materiales intermedios (escala de
grises) y así eliminar (disminuir) el posprocesamiento.
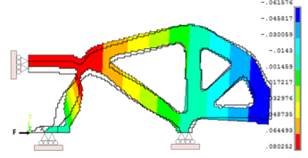
a) Simulación de la topología 2D con posprocesamiento
básico (obtenida de la Fig. 7c).
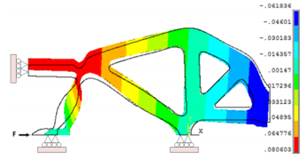
b) Simulación de la topología 2D suavizada (obtenida
de la Fig. 8a).
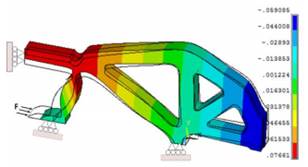
c) Simulación de la topología suavizada 3D (obtenida
a partir de la Fig. 8b).
Fig.
9.
Desplazamientos verticales (Y) en la parte simétrica de la pinza obtenidos con
ANSYS®.
3.3
Manufactura
del prototipo
En
la Fig. 10 se muestra un prototipo funcional de la topología 3D (ver Fig. 9c)),
el cual es manufacturado como se indicó en la sección 2.4. Un prototipo funcional
es capaz de mostrar las características y patrones de comportamiento del
producto final, aun cuando no dé valores exactos de su comportamiento. La Fig.
11 muestra una superposición de imágenes del prototipo sometido a una carga 𝐹 y sin ella,
donde se verifica el comportamiento adecuado del MF tipo pinza. Se observa que
bajo la acción de la carga 𝐹 la estructura del MF
se deforma y se cierra la mordaza de la pinza, lo cual era lo esperado. Sin
embargo, el desplazamiento es pequeño debido a varios factores. Uno de ellos se
debe a que la impresión del prototipo con el ABS se hace por capas con finas líneas
del polímero entrecruzadas, lo cual rigidiza la pieza. Otro factor que influye
en el desempeño del prototipo son el tipo de condiciones de fronteras, ya que
difieren un poco las usadas en el modelo (rodillos) y las del prototipo
(empotramiento). Finalmente, debido al orden de los desplazamientos del MF,
éstos se recomiendan para uso en la escala micro y nano.
Tabla
3.
Desplazamientos en el punto de salida de interés 𝑢𝑜𝑢𝑡.
4. CONCLUSIONES
El
diseño de un MF tipo pinza abordado mediante el modelo de diseño tradicional de
Pahl y Beitz resulta adecuado, ya que disminuye el ensayo y error, sistematiza
el proceso y conduce a diseños más fiables y en menor tiempo.
Con
el fin de disminuir la heurística en el modelo de diseño considerado, se usa el
MOT. El MOT es un método de optimización que permite el diseño conceptual de
MFs de forma rápida y con resultados adecuados. Tan general es el método que
con solo cambiar el dominio de diseño y condiciones de carga y frontera, se
puede obtener diseños más complejos y novedosos desde el punto de vista de su geometría.
Además, el MOT puede ser usado en diversidad de problemas y no solo en el de maximizar
el desplazamiento, como se hizo en este trabajo.
La
etapa de diseño de detalle en el modelo de Pahl y Beitz se lleva a cabo con una
serie de posprocesamientos aplicados a la topología y que disminuyen la
complejidad de la misma haciéndola apta para su posterior manufactura por
prototipado rápido.
Un
prototipo funcional impreso en ABS con una impresora 3D se obtuvo, con el cual
se verificó el adecuado funcionamiento del MF tipo pinza y concluyó el modelo
de diseño abordado con una correcta solución al problema inicialmente planteado.
La
integración de tecnologías de punta, como lo es el MOT y la manufactura aditiva
dentro de un modelo de diseño tradicional, hacen que éste sea más eficiente, se
generen diseños óptimos y se reduzca costos en el proceso de diseño, puesto que
el tiempo de desarrollo del producto disminuye, se puede ahorrar material en la
manufactura y la elaboración de planos en el diseño de detalle ya no es
necesario.
5.
AGRADECIMIENTOS
El
primer autor agradece a la Universidad Nacional de Colombia por la financiación
de su maestría durante el 2011 y 2012 con el programa “Beca Estudiantes
Sobresalientes de Posgrado”, con la cual se desarrolló parte de este trabajo.
El segundo autor agradece a Colciencias el financiamiento parcial de su
maestría con el Programa Jóvenes Investigadores 2011.

Fig. 10. Prototipo funcional
en ABS del MF tipo pinza fabricado con manufactura aditiva (FDM).
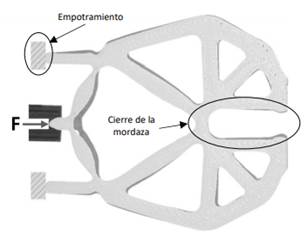
Fig. 11. Prototipo funcional
del MF tipo pinza. Gris claro: estructura sin carga. Gris oscuro: estructura cargada
y deformada.
6. Referencias Bibliográficas
[1]
Kota, S., Compliant systems using monolithic mechanisms, Smart Mater. Bull., 3,
7–10, 2001.
[2]
Howell, L.L., Magleby, S. P. y Olsen, B. M., Handbook of compliant mechanisms,
John Wiley & Sons, United Kingdom, 2013.
[3]
Gad-el-Hak, M., The MEMS handbook, 2a ed. Taylor & Francis, Boca Raton,
FL., 2006.
[4]
Vogel, S., Cats’ paws and catapults: mechanical worlds of nature and people. WW
Norton & Co., New York, 1998.
[5]
Ramírez-Gil, F.J., Diseño óptimo de micromecanismos tridimensionales con actuación
lectrotérmica utilizando optimización topológica y unidades de procesamiento
gráfico (GPU) [Tesis de maestría], Medellín, Colombia, Universidad Nacional de
Colombia, 2013.
[6]
Sepúlveda-Orozco, E. Diseño de un colector de energía piezoeléctrico (energy
harvesting) mediante optimización topológica que maximice la transformación de
energía mecánica en eléctrica generada por un ser humano al caminar”, [Tesis de
maestría], Medellín, Colombia, Universidad Nacional de Colombia, 2015.
[7]
Lobontiu, N., Compliant mechanisms: design of flexure hinges, CRC Press, Boca
Raton, 2003.
[8]
Smith, S.T., Flexures: elements of elastic mechanisms, Gordon & Breach, Amsterdam,
2000.
[9]
Bendsøe, M.P. y Sigmund, O., Topology optimization: theory, methods, and
applications, Springer, 2 a Ed., Berlin, 2003.
[10]
Pahl, G., Beitz, W., Feldhusen, J. y Grote, K.H., Engineering design: a
systematic approach, Springer, London, 2007.
[11]
Ma, Z.D., Wang, H., Kikuchi, N., Pierre, C. y Raju, B. Experimental validation
and prototyping of optimum designs obtained from topology optimization, Struct.
Multidiscip. Optim., 31, (5), 333–343, 2006.
[12]
Cross, N., Engineering design methods: strategies for product design, Wiley,
New York, 2000.
[13]
Narváez, C.A. y Garzón-Alvarado, D.A., Síntesis topológica de mecanismos
flexibles para aplicaciones biomédicas, Rev. Cuba. Investig. Bioméd., 29 (1),
1–16, 2010.
[14]
Napieralski, A., Napieralska, M., Szermer, M. y Maj, C., The evolution of MEMS
and modelling methodologies, Int. J. Comput. Math. Electr. Electron. Eng., 31
(5), 1458–1469, 2012.
[15]
Deepak, S.R., Dinesh, M., Sahu, D.K. y Ananthasuresh, G.K., A comparative study
of the formulations and benchmark problems for the topology optimization of
compliant mechanisms, J. Mech. Robot., 1(1), 1–8, 2008.
[16]
Howell, L. y Midha, A., Parametric deflection approximations for initially
curved, largedeflection beams in compliant mechanisms, en ASME Design
Engineering Technical Conferences, Irvine, California, USA, 1996.
[17]
Ananthaturesh, G.K., Kota, S. y Gianchandani, Y., A methodical approach to the
synthesis of compliant micromechanisms. En: V IEEE SolidState ensors and
Actuators Workshop, Hilton Head Island, SC, USA, 189–192,1994.
[18]
Bendsøe, M. y Sigmund, O., Material interpolation schemes in topology
optimization, Arch. Appl. Mech., 69 (9), 635–654, 1999.
[19]
Cardoso, E.L. y Fonseca, J.S.O., Complexity control in the topology
optimization of continuum structures, J. Braz. Soc. Mech. Sci. Eng., 25 (3), 293–301,
2003.
[20]
Sigmund O. y Petersson, J., Numerical instabilities in topology optimization: A
survey on procedures dealing with checkerboards, eshdependencies and local
minima, Struct. Optim., 16 (1), 68–75, 1998.
[21]
Zhang, Y., Solving large-scale linear programs by interior-point methods under
the Matlab environment, Optim. Methods Softw., 10 (1), 1– 31, 1998.
[22]
Haftka, R.T. y Gürdal, Z., Elements of structural optimization, Springer, 3a
ed., 1992.
[23]
Ramírez, F., Sepúlveda, E. y Montealegre, W., Diseño de mecanismos flexibles
mediante el método de optimización topológica. En: Métodos numéricos y sus
aplicaciones en diferentes áreas, Cali, Colombia, UAO, 545– 552, Agosto, 2013.
[24]
Tovar, A., Optimización topológica con la técnica de los autómatas celulares
híbridos, Rev. Int. Métod. Numér. Para Cálculo Diseño En Ing., 21 (4), 365–383,
2005.
[25]
Sigmund, O., On the design of compliant mechanisms using topology optimization,
Mech. Struct. Mach., 25 (4), 493–524, 1997.
[26]
Vatanabe, S.L., Montealagre, W. y Silva, E.C.N., Modeling of functionally
graded materials. En: Comprehensive materials processing, Elsevier, 261–282,
2014.
[27]
Gibson, I., Rosen, D. y Stucker, B., Additive manufacturing technologies: 3D
printing, rapid prototyping, and direct digital manufacturing, Springer, New
York, 2015.
[28]
Stratasys Ltd, How FDM 3D Printing Works.Disponible en: http://www.stratasys.com/3dprinters/technologies/fdm-technology. [Consultado
el 07-sep-2016].
[29]
Sigmund, O., A 99 line topology optimization code written in Matlab, Struct.
Multidiscip. Optim., 21 (2), 120–127, 2001.
[30]
Méndez-Algarra, G.A. y Tovar, A., Integrating topology and shape optimization:
a way to reduce weight in structural ship design, Ship Sci. Technol., 3 (5),
83–92, 2009.


![]()
![]() = 𝑢
= 𝑢![]() − 𝑢
− 𝑢![]() , Δ𝑢
, Δ𝑢![]() = 𝑢
= 𝑢![]() − 𝑢
− 𝑢![]() y 𝜀 es una tolerancia dada,
normalmente una fracción de la función objetivo cuando la estructura está completamente
sólida. Si la tolerancia no se alcanza antes de un número máximo de iteraciones
𝑘𝑚𝑎𝑥, entonces
el algoritmo termina. En las siguientes subsecciones se presenta el problema de
optimización topológica aplicado al diseño de MFs y el modelo de material SIMP.
y 𝜀 es una tolerancia dada,
normalmente una fracción de la función objetivo cuando la estructura está completamente
sólida. Si la tolerancia no se alcanza antes de un número máximo de iteraciones
𝑘𝑚𝑎𝑥, entonces
el algoritmo termina. En las siguientes subsecciones se presenta el problema de
optimización topológica aplicado al diseño de MFs y el modelo de material SIMP.
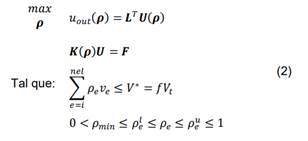
![]()